目录
一、活动安排问题
二、最优装载问题
三、分数背包问题
四、多机调度问题
一、活动安排问题
1、策略
活动安排问题:设有n个活动的集合E={1,2,...,n},每个活动i都有一个使用该资源的起始时间和一个结束时间
,且
。如果选择了活动i则它在时间区间
内占用资源,如何在有限的时间内选择最多的活动方案安排。
解法:按结束时间优先的贪心算法。
(1) 如果活动i和活动j能够相容,假设活动i在活动j之前,那么一定有。
(2)按照序列对
和
同时进行排序,保证两者对应。排序可以使用快速排序、归并排序和堆排复杂度为O(nlogn)。
(3)第1个活动最小,所以进入活动安排,其他如果存在
,则i=j,移动活动安排。
给定一个活动序列 的关系:
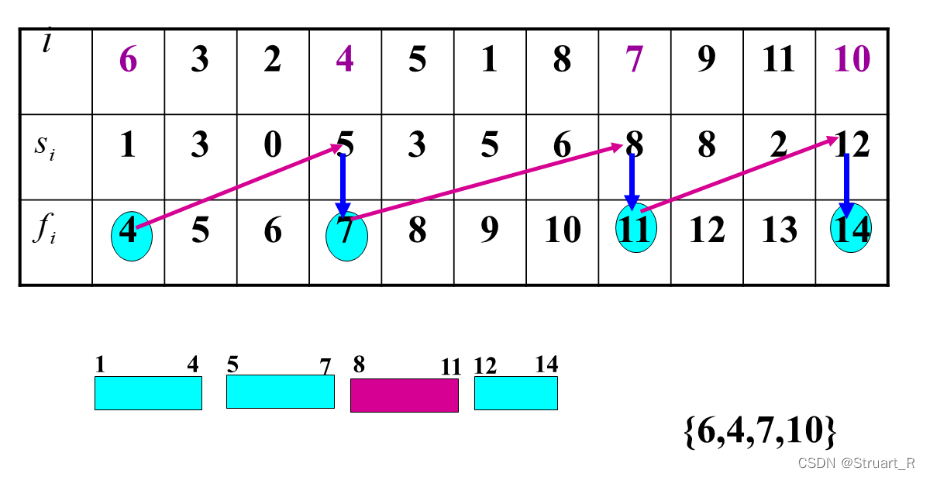
2、代码
//活动安排
import java.util.Scanner;
public class activityarrangement {
public static void main(String[] args)
{
int n=new Scanner(System.in).nextInt();
int s[]=new int[n];
int f[]=new int[n];
for(int i=0;i<n;i++)
s[i]=new Scanner(System.in).nextInt();
for(int i=0;i<n;i++)
f[i]=new Scanner(System.in).nextInt();
quickSort(f,s, 0, n-1);
GreedySelector(s,f);
}
public static void GreedySelector(int s[],int f[])
{
System.out.println(s[0]+" "+f[0]);
int j=0;
for(int i=1;i<s.length;i++)
{
if(s[i]>=f[j])
{
System.out.println(s[i]+" "+f[i]);
j=i;
}
}
}二、最优装载问题
1、策略
有一批集装箱要装上一艘载重为c的轮船,集装箱i的重量为,要求装载体积不受限制情况下,将尽可能多的集装箱装上轮船。
利用贪心算法,重量最轻的集装箱优先装载,直到轮船载重无法继续装入集装箱。
排序方法可以使用快排、归排和堆排来降低时间复杂度。
约束条件和目标函数如下:

例题如下:

2、代码
//最优装载问题
public static void main(String []args)
{
int c=400;
int weights[]={100,200,50,90,150,50,20,80};
quickSort(weights,0,weights.length-1);
System.out.println(load(weights,c));
}
public static int load(int weights[],int c)
{
int tmp=c;
for(int i=0;i<weights.length;i++)
{
if(c>weights[i])
{
c-=weights[i];
}
}
return tmp-c;
} 三、分数背包问题
1、策略
分数背包问题:在0-1背包的问题基础上,可以每个物品装一部分,即0~1背包问题,要求在有限的容量基础上,求解装有物品的最高总价值。
策略:以单位重量价值最高的优先的贪心算法。
建立a数组(单位重量下价值),以a数组为排序依据,同时排序a,w,v数组,计算a数组较大值优先的情况下能产生的最大总价值。
例题如下:

2、代码
(省略排序过程)
//分数背包问题
public class dividebackage {
public static void main(String[] args)
{
int n=3;
int c=20;
double w[]={18,15,10};
double v[]={25,24,15};
double a[]=new double[n];
for(int i=0;i<n;i++)
a[i]=v[i]/w[i];
quickSort(a,w,v,0,w.length-1);
System.out.println(maximum(a,w,v,c));
}
public static double maximum(double a[],double w[],double v[],int c)
{
double value=0;
int weight=0;
for(int i=a.length-1;i>=0;i--)
{
if((c-weight)>=w[i])
{
value+=v[i];
weight+=w[i];
}
else
{
value+=v[i]*(c-weight)/w[i];
break;
}
}
return value;
}
}四、多机调度问题
1、概述
多机调度问题:设有n个独立作业,由m台相同机器进行加工处理,作业i所需的处理时间为,每个作业均可以在任何一台机器上加工处理,但不可间断、拆分。设计一种算法,使得n个作业在尽可能短的时间内由m台机器加工处理完成。
策略:按任务时间较长的进行贪心算法,设定time,p,d,m,s五个数组(定义看下面代码注释),首先对time数组和p数组按任务时间降序排序(快排),调度问题为添加任务和时间推移两个阶段循环进行,直到任务不再添加,所有机器还需占用时间数为0,则退出调度问题。
添加任务:遍历每一个机器,若当前机器m还需占用时间为0,且仍有任务i需要添加,则将任务i添加到机器m,机器m的所做任务数加一,机器m执行任务添加任务i编号。
时间推移:时间后移一,每个任务的还需所占用时间减一,若每个机器的所占用时间都为0且没有新任务添加,则退出调度问题,返回当前时间。若存在机器i所占用时间为0,但仍有其他机器任务未结束,则机器i占用时间不再减少,避免出现负数。
下面例题解决效果:

2、代码
//多机调度问题
public class multimachine {
public static void main(String[] args)
{
int time[]={2,14,4,16,6,5,3}; //每个任务所占时间
int p[]={1,2,3,4,5,6,7}; //任务编号
int d[]={0,0,0}; //当前机器还需占用时间数
int m[]={0,0,0}; //每个机器执行了几个任务
int s[][]=new int[d.length][time.length]; //每个机器执行了哪些任务
//对时间列和任务编号进行重新排序
quickSort(time,p,0,time.length-1);
//输出多机调度总时间
deploy(time,p,d,s,m);
//输出每个机器执行了哪些任务
for(int i=0;i<d.length;i++)
{
for(int j=0;j<time.length;j++)
{
if(s[i][j]==0)
break;
System.out.print(s[i][j]+" ");
}
System.out.println("");
}
}
public static void deploy(int time[],int p[],int d[],int s[][],int m[])
{
int tot=0;
int c=0; //总作业序列顺序执行到几个
while(true)
{
//进入任务,增加每个机器的所占用时间
for(int i=0;i<d.length;i++)
{
if(d[i]==0&&c<time.length)
{
d[i]+=time[c];
s[i][m[i]++]=p[c++];
}
}
tot+=1;
int zero=0;
//时间推移加一,减少每个机器的所占用时间
for(int i=0;i<d.length;i++)
{
if(d[i]==0)
break;
d[i]--;
zero+=d[i];
}
//若每个机器都为0,且没有任务继续添加,则终止调度
if(zero==0)
break;
}
System.out.println(tot);
}