⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️
🐴作者:秋无之地🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。
🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、留言💬、关注🤝,关注必回关
一、确定目标
这次的目标是:使用Python编写八大排序算法,并且比较一下各种排序算法在真实场景下的运行速度。
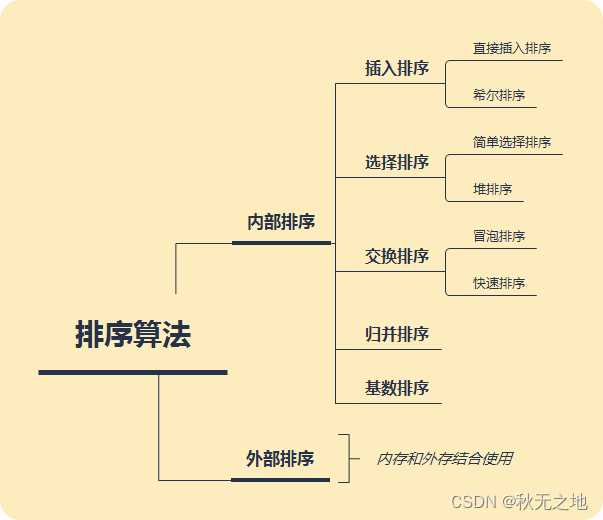
二、算法比较
1、直接插入排序
- 时间复杂度:O(n²)
- 空间复杂度:O(1)
- 稳定性:稳定
def insert_sort(array):
for i in range(len(array)):
for j in range(i):
if array[i] < array[j]:
array.insert(j, array.pop(i))
break
return array2、希尔排序
- 时间复杂度:O(n)
- 空间复杂度:O(n√n)
- 稳定性:不稳定
def shell_sort(array):
gap = len(array)
while gap > 1:
gap = gap // 2
for i in range(gap, len(array)):
for j in range(i % gap, i, gap):
if array[i] < array[j]:
array[i], array[j] = array[j], array[i]
return array3、简单选择排序
- 时间复杂度:O(n²)
- 空间复杂度:O(1)
- 稳定性:不稳定
def select_sort(array):
for i in range(len(array)):
x = i # min index
for j in range(i, len(array)):
if array[j] < array[x]:
x = j
array[i], array[x] = array[x], array[i]
return array4、堆排序
- 时间复杂度:O(nlog₂n)
- 空间复杂度:O(1)
- 稳定性:不稳定
def heap_sort(array):
def heap_adjust(parent):
child = 2 * parent + 1 # left child
while child < len(heap):
if child + 1 < len(heap):
if heap[child + 1] > heap[child]:
child += 1 # right child
if heap[parent] >= heap[child]:
break
heap[parent], heap[child] = \
heap[child], heap[parent]
parent, child = child, 2 * child + 1
heap, array = array.copy(), []
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0:
heap[0], heap[-1] = heap[-1], heap[0]
array.insert(0, heap.pop())
heap_adjust(0)
return array5、冒泡排序
- 时间复杂度:O(n²)
- 空间复杂度:O(1)
- 稳定性:稳定
def bubble_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]:
array[i], array[j] = array[j], array[i]
return array6、快速排序
- 时间复杂度:O(nlog₂n)
- 空间复杂度:O(nlog₂n)
- 稳定性:不稳定
def quick_sort(array):
def recursive(begin, end):
if begin > end:
return
l, r = begin, end
pivot = array[l]
while l < r:
while l < r and array[r] > pivot:
r -= 1
while l < r and array[l] <= pivot:
l += 1
array[l], array[r] = array[r], array[l]
array[l], array[begin] = pivot, array[l]
recursive(begin, l - 1)
recursive(r + 1, end)
recursive(0, len(array) - 1)
return array7、归并排序
- 时间复杂度:O(nlog₂n)
- 空间复杂度:O(1)
- 稳定性:稳定
def merge_sort(array):
def merge_arr(arr_l, arr_r):
array = []
while len(arr_l) and len(arr_r):
if arr_l[0] <= arr_r[0]:
array.append(arr_l.pop(0))
elif arr_l[0] > arr_r[0]:
array.append(arr_r.pop(0))
if len(arr_l) != 0:
array += arr_l
elif len(arr_r) != 0:
array += arr_r
return array
def recursive(array):
if len(array) == 1:
return array
mid = len(array) // 2
arr_l = recursive(array[:mid])
arr_r = recursive(array[mid:])
return merge_arr(arr_l, arr_r)
return recursive(array)8、基数排序
- 时间复杂度:O(d(r+n))
- 空间复杂度:O(rd+n)
- 稳定性:稳定
def radix_sort(array):
bucket, digit = [[]], 0
while len(bucket[0]) != len(array):
bucket = [[], [], [], [], [], [], [], [], [], []]
for i in range(len(array)):
num = (array[i] // 10 ** digit) % 10
bucket[num].append(array[i])
array.clear()
for i in range(len(bucket)):
array += bucket[i]
digit += 1
return array三、速度比较
如果数据量特别大,采用分治算法的快速排序和归并排序,可能会出现递归层次超出限制的错误。
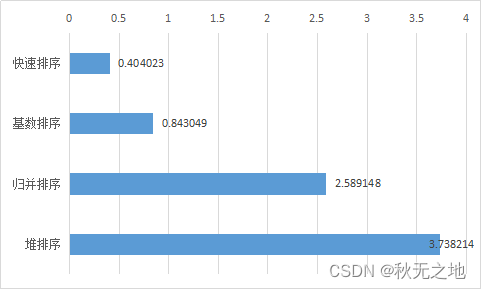
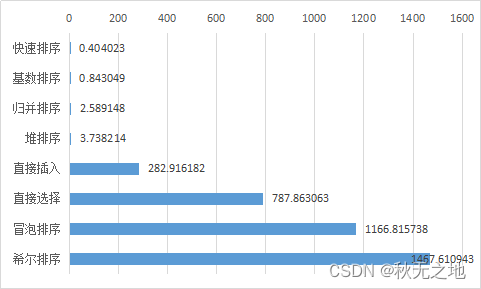
1、算法执行时间
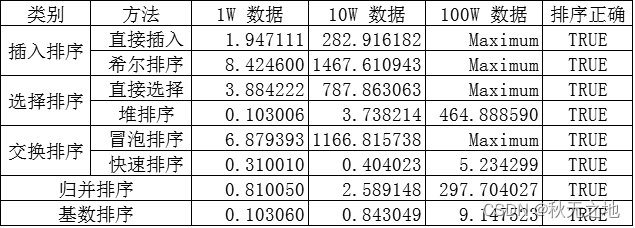
2、算法速度比较
四、总结
- 从速度来看,快速排序的耗时最短;
- 从稳定性来看,直接插入、冒泡、归并、基数等排序相对稳定;
- 从代码复杂度来看,冒泡排序最简单。
版权声明
本文章版权归作者所有,未经作者允许禁止任何转载、采集,作者保留一切追究的权利。