文章目录
- abstract
- 两种余项型泰勒公式的对比和总结
- Maclaurin公式
- 常用函数的Maclaurin公式
- 推导
- 例
- 求极限
- 按幂展开
abstract
- 泰勒公式的两种余项型(Penao&Lagrange)泰勒公式的对比和总结
- 常用的Maclaurin公式列举(Peano余项型为主)
两种余项型泰勒公式的对比和总结
-
Taylor公式 Lagrange型 Peano项 Note 条件 [ a , b ] [a,b] [a,b]上有 n n n阶连续导数, ( a , b ) (a,b) (a,b)内存在 n + 1 n+1 n+1阶导数 x = x 0 x=x_0 x=x0处存在 n n n阶导数 前者对 f ( x ) f(x) f(x)要求较高 余项 R n ( x ) R_n(x) Rn(x)= f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(ξ)(x−x0)n+1或 f ( n + 1 ) ( θ x ) ( n + 1 ) ! ( x − x 0 ) n + 1 \frac{f^{(n+1)}(\theta x)}{(n+1)!}(x-x_0)^{n+1} (n+1)!f(n+1)(θx)(x−x0)n+1, θ ∈ ( 0 , 1 ) \theta\in(0,1) θ∈(0,1) R n ( x ) R_n(x) Rn(x)= o ( ( x − x 0 ) n ) o((x-x_0)^{n}) o((x−x0)n) 前者余项具体,后者仅表达了高阶无穷小 用途 可用于区间 [ a , b ] [a,b] [a,b]上,例如证明不等式或等式,估计逼近误差 仅用于 x 0 x_0 x0的邻域 U ( x 0 ) U(x_0) U(x0),例如讨论极值,求解 x → x 0 x\to{x_0} x→x0时的极限 后者用在某些条件下的求极限问题上,可以带来方便
Maclaurin公式
- 这里主要讨论Peano型Maclaurin公式(一般不要求计算误差精度,Peano型足够使用)
-
f
(
x
)
f(x)
f(x)=
f
(
0
)
+
f
′
(
0
)
x
+
1
2
!
f
′
′
(
0
)
x
2
f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2
f(0)+f′(0)x+2!1f′′(0)x2+
⋯
\cdots
⋯+
1
n
!
f
(
n
)
(
0
)
x
n
\frac{1}{n!}f^{(n)}(0)x^n
n!1f(n)(0)xn+
R
n
(
x
)
R_n(x)
Rn(x)
(1),两种余项分别为:-
R
n
(
x
)
R_n(x)
Rn(x)=
o
(
x
n
)
o(x^{n})
o(xn)
(1-1) -
R
n
(
x
)
R_n(x)
Rn(x)=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}
(n+1)!f(n+1)(ξ)(x−x0)n+1或
f
(
n
+
1
)
(
θ
x
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
\frac{f^{(n+1)}(\theta x)}{(n+1)!}(x-x_0)^{n+1}
(n+1)!f(n+1)(θx)(x−x0)n+1,
θ
∈
(
0
,
1
)
\theta\in(0,1)
θ∈(0,1)
(1-2)
-
R
n
(
x
)
R_n(x)
Rn(x)=
o
(
x
n
)
o(x^{n})
o(xn)
常用函数的Maclaurin公式
-
主要掌握展开公式的前几项(2到5项,一般3项)就足够一般的应用,
-
只要知道公式
(1),和 f ( x ) f(x) f(x)的高阶导数,在必要的时候可以自行计算更多的项- e x e^{x} ex= 1 + x + 1 2 ! x 2 + ⋯ + 1 n ! x n 1+x+\frac{1}{2!}x^2+\cdots+\frac{1}{n!}x^{n} 1+x+2!1x2+⋯+n!1xn+ o ( x n ) o(x^{n}) o(xn)
- sin x \sin{x} sinx= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n − 1 ) ! x 2 n − 1 \frac{(-1)^{n}}{(2n-1)!}x^{2n-1} (2n−1)!(−1)nx2n−1+ o ( x 2 n − 1 ) o(x^{2n-1}) o(x2n−1)
- cos x \cos{x} cosx= 1 − 1 2 ! x 2 + 1 4 ! x 4 − 1 6 ! x 6 1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^{6} 1−2!1x2+4!1x4−6!1x6+ ⋯ \cdots ⋯+ ( − 1 ) n ( 2 n ) ! x 2 n \frac{(-1)^{n}}{(2n)!}x^{2n} (2n)!(−1)nx2n+ o ( x 2 n ) o(x^{2n}) o(x2n)
- ln ( 1 + x ) \ln{(1+x)} ln(1+x)= x − x 2 2 + x 3 3 − x 5 5 x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^5}{5} x−2x2+3x3−5x5+ ⋯ \cdots ⋯+ ( − 1 ) n − 1 x n n (-1)^{n-1}\frac{x^{n}}{n} (−1)n−1nxn+ o ( x n ) o(x^{n}) o(xn)
- ( 1 + x ) m (1+x)^{m} (1+x)m= 1 + m x + m ( m − 1 ) 2 ! x 2 1+mx+\frac{m(m-1)}{2!}x^2 1+mx+2!m(m−1)x2+ ⋯ \cdots ⋯+ m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n \frac{m(m-1)\cdots(m-n+1)}{n!}x^{n} n!m(m−1)⋯(m−n+1)xn+ o ( x n ) o(x^{n}) o(xn)
-
其中偶(奇)函数的展开式也是偶(奇)函数
- 上述公式3,4有时也写作
-
sin
x
\sin{x}
sinx=
x
−
1
3
!
x
3
+
1
5
!
x
5
−
1
7
!
x
7
x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7}
x−3!1x3+5!1x5−7!1x7+
⋯
\cdots
⋯+
(
−
1
)
n
(
2
n
+
1
)
!
x
2
n
+
1
\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}
(2n+1)!(−1)nx2n+1+
o
(
x
2
n
+
2
)
o(x^{2n+2})
o(x2n+2)
- 余项前的一项的幂是奇次幂 k k k即可( 2 n + 1 2n+1 2n+1或 2 n − 1 2n-1 2n−1),Peano余项的幂次数可以 o ( x k ) o(x^{k}) o(xk)或 o ( x k + 1 ) o(x^{k+1}) o(xk+1)
-
cos
x
\cos{x}
cosx=
1
−
1
2
!
x
2
+
1
4
!
x
4
−
1
6
!
x
6
1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^{6}
1−2!1x2+4!1x4−6!1x6+
⋯
\cdots
⋯+
(
−
1
)
n
(
2
n
)
!
x
2
n
\frac{(-1)^{n}}{(2n)!}x^{2n}
(2n)!(−1)nx2n+
o
(
x
2
n
+
1
)
o(x^{2n+1})
o(x2n+1)
- 余项前的一项的幂是偶次幂,通常表示为 2 n 2n 2n,Peano余项的幂次数可以是 o ( x 2 n ) o(x^{2n}) o(x2n)或 o ( x 2 n + 1 ) o(x^{2n+1}) o(x2n+1)
-
sin
x
\sin{x}
sinx=
x
−
1
3
!
x
3
+
1
5
!
x
5
−
1
7
!
x
7
x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7}
x−3!1x3+5!1x5−7!1x7+
⋯
\cdots
⋯+
(
−
1
)
n
(
2
n
+
1
)
!
x
2
n
+
1
\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}
(2n+1)!(−1)nx2n+1+
o
(
x
2
n
+
2
)
o(x^{2n+2})
o(x2n+2)
- 上述公式3,4有时也写作
-
其中余项不是 x n x^{n} xn的公式都是经过简并后的公式(把值为0的项隐后剩下的项重新编排 i = 0 , 1 , 2 , i=0,1,2, i=0,1,2,)
-
注意到,上述公式挂等号的前提是带上余项,反之,带上余项的展开式可以直接被展开函数参与某这些运算(比如求极限)
推导
-
按照 f ( x ) f(x) f(x)的 n n n阶导数公式和 f ( x ) f(x) f(x)的 n n n阶Maclaurin公式推导即可
-
以 sin x \sin{x} sinx为例推导:
-
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)=
(
sin
x
)
(
n
)
(\sin{x})^{(n)}
(sinx)(n)=
sin
(
x
+
n
π
2
)
\sin{(x+\frac{n\pi}{2})}
sin(x+2nπ);
(2-1) -
f
(
n
)
(
0
)
f^{(n)}(0)
f(n)(0)=
(
sin
x
)
(
n
)
∣
x
=
0
(\sin{x})^{(n)}|_{x=0}
(sinx)(n)∣x=0=
sin
(
n
π
2
)
\sin{(\frac{n\pi}{2})}
sin(2nπ)
(2-2)
n n n f ( n ) ( 0 ) f^{(n)}(0) f(n)(0) 0 0 1 1 1 1 2 0 3 -1 4 0 5 1 6 0 ⋯ \cdots ⋯ ⋯ \cdots ⋯ 根据上述列举和三角函数的知识可知, f ( n ) ( 0 ) f^{(n)}(0) f(n)(0), n = 0 , 1 , 2 , ⋯ n=0,1,2,\cdots n=0,1,2,⋯会循环得取4个数 0 , 1 , 0 , − 1 0,1,0,-1 0,1,0,−1,j记为序列
(S1)有Maclaurin公式可知, f ( n ) ( 0 ) = 0 f^{(n)}(0)=0 f(n)(0)=0的项也是0,这些项可以被简并不写-
这样一来,由序列(S1),保留下来的项的幂的次数就不是连续的了,相邻项的次数相差2而不是1
-
不妨设 p n ( x ) p_{n}(x) pn(x)= ∑ i = 0 n a i x n \sum_{i=0}^{n}a_ix^{n} ∑i=0naixn,
- 前 k k k个非0项分别为 a 1 , a 3 , ⋯ , a 2 k − 1 a_1,a_3,\cdots,a_{2k-1} a1,a3,⋯,a2k−1, a 2 i − 1 , i = 1 , ⋯ , k a_{2i-1},i=1,\cdots,k a2i−1,i=1,⋯,k都是非0项
- 另一方面, f ( x ) = a 0 , a 2 , ⋯ , a 2 k f(x)=a_0,a_2,\cdots,a_{2k} f(x)=a0,a2,⋯,a2k都是0
- ∑ i = 0 k a 2 k − 1 \sum_{i=0}^{k}a_{2k-1} ∑i=0ka2k−1= ∑ i = 0 2 k a i \sum_{i=0}^{2k}a_{i} ∑i=02kai即消去0项之前, 2 k − 1 2k-1 2k−1阶泰勒多项式和 2 k 2k 2k阶泰勒多相式相等(余项可以表示为 o ( x 2 k ) o(x^{2k}) o(x2k)
- 为了便于讨论,将 p n ( x ) p_n(x) pn(x)消去0项后的公式记为 q m ( x ) q_m(x) qm(x)= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 + ⋯ x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7}+\cdots x−3!1x3+5!1x5−7!1x7+⋯的项,第 m = 1 , 2 , ⋯ m=1,2,\cdots m=1,2,⋯项记为 b m b_m bm,它们全部对应于非零项,并且容易归纳出: q n ( x ) q_{n}(x) qn(x)的通项 b m = ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 b_m=\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} bm=(2m−1)!(−1)m−1x2m−1,次数 2 m − 1 2m-1 2m−1表示该项对应于 p n ( x ) p_n(x) pn(x)中的 2 m − 1 2m-1 2m−1次幂的项(非0),而 n = 2 m n=2m n=2m项则是零项
- 此时将 q m ( x ) q_m(x) qm(x)表示为 q m ( x ) q_m(x) qm(x)= x − 1 3 ! x 3 + 1 5 ! x 5 − 1 7 ! x 7 x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7} x−3!1x3+5!1x5−7!1x7+ ⋯ \cdots ⋯+ ( − 1 ) m − 1 ( 2 m − 1 ) ! x 2 m − 1 \frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1} (2m−1)!(−1)m−1x2m−1
- 取 m = k m=k m=k,可以得到 2 k − 1 2k-1 2k−1次泰勒多项式
-
sin
x
\sin{x}
sinx=
x
−
1
3
!
x
3
+
1
5
!
x
5
−
1
7
!
x
7
x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}-\frac{1}{7!}x^{7}
x−3!1x3+5!1x5−7!1x7+
⋯
\cdots
⋯+
(
−
1
)
m
−
1
(
2
m
−
1
)
!
x
2
m
−
1
\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1}
(2m−1)!(−1)m−1x2m−1+
R
2
m
R_{2m}
R2m
(3)
-
Lagrange余项:由式(1-2),(2-1),可知 R 2 m ( x ) R_{2m}(x) R2m(x)= sin ( θ x + ( 2 m + 1 ) π 2 ) ( 2 m + 1 ) ! x 2 m + 1 \frac{\sin(\theta{x}+(2m+1)\frac{\pi}{2})}{(2m+1)!}x^{2m+1} (2m+1)!sin(θx+(2m+1)2π)x2m+1
(4)-
t
(
x
)
t(x)
t(x)=
sin
(
θ
x
+
(
2
m
+
1
)
π
2
)
\sin(\theta{x}+(2m+1)\frac{\pi}{2})
sin(θx+(2m+1)2π)=
sin
(
θ
x
+
m
π
+
π
2
)
\sin(\theta{x}+m\pi+\frac{\pi}{2})
sin(θx+mπ+2π)
- 当 m m m为奇数时, t ( x ) t(x) t(x)= sin ( θ x + π + π 2 ) \sin(\theta{x+\pi+\frac{\pi}{2}}) sin(θx+π+2π)= sin ( θ x − π 2 ) \sin(\theta{x}-\frac{\pi}{2}) sin(θx−2π)= − cos θ x -\cos\theta{x} −cosθx
- 当 m m m为偶数时, t ( x ) t(x) t(x)= sin ( θ x + π 2 ) \sin(\theta{x}+\frac{\pi}{2}) sin(θx+2π)= cos θ x \cos\theta{x} cosθx
- 可以用 ( − 1 ) m (-1)^{m} (−1)m归纳上述符号变化,从而 t ( x ) t(x) t(x)= ( − 1 ) m cos θ x (-1)^{m}\cos{\theta{x}} (−1)mcosθx
- 从而
R
2
m
(
x
)
R_{2m}(x)
R2m(x)=
(
−
1
)
m
cos
θ
x
(
2
m
+
1
)
!
x
2
m
+
1
(-1)^{m}\frac{\cos{\theta{x}}}{(2m+1)!}x^{2m+1}
(−1)m(2m+1)!cosθxx2m+1,
θ
∈
(
0
,
1
)
\theta\in(0,1)
θ∈(0,1)
(4-1)
-
t
(
x
)
t(x)
t(x)=
sin
(
θ
x
+
(
2
m
+
1
)
π
2
)
\sin(\theta{x}+(2m+1)\frac{\pi}{2})
sin(θx+(2m+1)2π)=
sin
(
θ
x
+
m
π
+
π
2
)
\sin(\theta{x}+m\pi+\frac{\pi}{2})
sin(θx+mπ+2π)
-
若取 m = 1 m=1 m=1,得近似公式 sin x ∼ x \sin{x}\sim{x} sinx∼x
- 代入(4-1),可知,此时误差为 ∣ R 2 ∣ = ∣ − cos θ x 3 ! x 3 ∣ ⩽ ∣ x ∣ 3 6 |R_2|=|-\frac{\cos\theta{x}}{3!}x^3|\leqslant{\frac{|x|^{3}}{6}} ∣R2∣=∣−3!cosθxx3∣⩽6∣x∣3,其中 ∣ cos θ x ∣ ⩽ 1 |\cos\theta{x}|\leqslant{1} ∣cosθx∣⩽1
-
若 m = 2 m=2 m=2,则可得到 3 3 3次泰勒多项式 ( x − x 3 3 ! ) (x-\frac{x^3}{3!}) (x−3!x3),误差 ∣ R 2 m ∣ ⩽ 1 5 ! ∣ x ∣ 5 |R_{2m}|\leqslant{\frac{1}{5!}|x|^{5}} ∣R2m∣⩽5!1∣x∣5
-
若 m = 3 m=3 m=3,则可得 5 5 5次泰勒多项式 ( x − x 3 3 ! + x 5 5 ! ) (x-\frac{x^3}{3!}+\frac{x^5}{5!}) (x−3!x3+5!x5),误差不超过 1 7 ! ∣ x ∣ 7 \frac{1}{7!}|x|^{7} 7!1∣x∣7
-
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)=
(
sin
x
)
(
n
)
(\sin{x})^{(n)}
(sinx)(n)=
sin
(
x
+
n
π
2
)
\sin{(x+\frac{n\pi}{2})}
sin(x+2nπ);
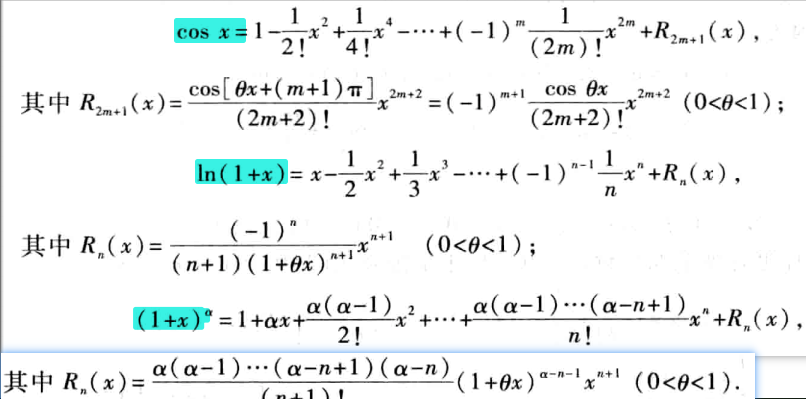
例
求极限
-
求 lim x → 0 sin x − x cos x sin 3 x \lim\limits_{x\to{0}}\frac{\sin{x}-x\cos{x}}{\sin^{3}x} x→0limsin3xsinx−xcosx=A
-
用 sin 3 x ∼ x 3 \sin^3{x}\sim{x^3} sin3x∼x3替换分母
-
解法1:利用等价无穷小替换分母,在利用洛必达法则求解
-
解法2:利用带有Peano余项的Maclaurin公式
- sin x \sin{x} sinx= x − x 3 3 ! + o ( x 3 ) x-\frac{x^3}{3!}+o(x^3) x−3!x3+o(x3);
- cos x = 1 − x 2 2 ! + o ( x 2 ) \cos{x}=1-\frac{x^2}{2!}+o(x^2) cosx=1−2!x2+o(x2); x cos x = x − x 3 2 ! + o ( x 3 ) x\cos{x}=x-\frac{x^3}{2!}+o(x^{3}) xcosx=x−2!x3+o(x3)
- 于是
sin
x
−
x
cos
x
\sin{x}-x\cos{x}
sinx−xcosx=
x
−
x
3
3
!
+
o
(
x
3
)
−
(
x
+
x
3
2
!
+
o
(
x
3
)
)
x-\frac{x^3}{3!}+o(x^{3})-(x+\frac{x^3}{2!}+o(x^3))
x−3!x3+o(x3)−(x+2!x3+o(x3))=
1
3
x
3
+
o
(
x
3
)
\frac{1}{3}x^3+o(x^{3})
31x3+o(x3)
- α ( x ) \alpha(x) α(x)的高阶无穷小 o ( α ( x ) ) , o 1 ( α ( x ) ) o(\alpha(x)),o_1(\alpha(x)) o(α(x)),o1(α(x))之间的和差运算结果仍然是 α ( x ) \alpha(x) α(x)的高阶无穷小( lim o ( α ( x ) ± o 1 ( α ( x ) ) ) α ( x ) \lim\frac{o(\alpha(x)\pm{o_1(\alpha(x))})}{\alpha(x)} limα(x)o(α(x)±o1(α(x)))=0)
- A = lim x → 0 1 3 x 3 + o ( x 3 ) x 3 A=\lim\limits_{x\to{0}}\frac{\frac{1}{3}x^3+o(x^3)}{x^3} A=x→0limx331x3+o(x3)= 1 3 \frac{1}{3} 31
-
按幂展开
f ( x ) = x 3 + 3 x 2 − 2 x + 4 f(x)=x^3+3x^2-2x+4 f(x)=x3+3x2−2x+4的按 ( x + 1 ) (x+1) (x+1)的升幂展开(升幂排列)
-
即按 ( x − ( − 1 ) ) (x-(-1)) (x−(−1))的展开, x 0 = − 1 x_0=-1 x0=−1,得到 g ( x ) g(x) g(x)= ∑ i = 0 3 a i ( x + 1 ) i \sum_{i=0}^{3}a_i(x+1)^{i} ∑i=03ai(x+1)i= ∑ i = 0 3 a i ( x − ( − 1 ) ) i \sum_{i=0}^{3}a_i(x-(-1))^{i} ∑i=03ai(x−(−1))i
-
计算 f ( k ) ( x 0 ) f^{(k)}(x_0) f(k)(x0);
-
由于 f ( x ) f(x) f(x)是个 n = 3 n=3 n=3次的多项式,其泰勒展开也是3次的
-
a i = f ( n ) ( x 0 ) i ! a_i=\frac{f^{(n)}(x_0)}{i!} ai=i!f(n)(x0), i = 0 , 1 , 2 , 3 i=0,1,2,3 i=0,1,2,3
-
a 0 = f ( x 0 ) a_0=f(x_0) a0=f(x0)= 8 8 8
-
f ′ ( x ) = 3 x 2 + 6 x − 2 ; f ′ ( − 1 ) = − 5 f'(x)=3x^2+6x-2;f'(-1)=-5 f′(x)=3x2+6x−2;f′(−1)=−5
-
f ′ ′ ( x ) = 6 x + 6 ; f ′ ′ ( − 1 ) = 0 f''(x)=6x+6;f''(-1)=0 f′′(x)=6x+6;f′′(−1)=0
-
f ( 3 ) ( x ) = 6 ; f ( 3 ) ( − 1 ) = 6 f^{(3)}(x)=6;f^{(3)}(-1)=6 f(3)(x)=6;f(3)(−1)=6
-
f ( k ) ( x ) = 0 ; ( k ⩾ 4 ) f^{(k)}{(x)}=0;(k\geqslant 4) f(k)(x)=0;(k⩾4)
- 所以 R = R 4 ( x ) = 0 R=R_4(x)=0 R=R4(x)=0
-
-
-
f ( x ) = f ( − 1 ) + f ′ ( − 1 ) 1 ! ( x + 1 ) f(x)=f(-1)+\frac{f'(-1)}{1!}(x+1) f(x)=f(−1)+1!f′(−1)(x+1)+ f ′ ′ ( − 1 ) 2 ! ( x + 1 ) 2 \frac{f''(-1)}{2!}(x+1)^2 2!f′′(−1)(x+1)2+ f ( 3 ) ( − 1 ) 3 ! ( x + 1 ) 3 + R 4 ( x ) \frac{f^{(3)}(-1)}{3!}{(x+1)^3}+R_4(x) 3!f(3)(−1)(x+1)3+R4(x)= 8 − 5 ( x + 1 ) + ( x + 1 ) 3 8-5(x+1)+(x+1)^3 8−5(x+1)+(x+1)3