30二叉树-了解二叉树

news2024/11/18 15:26:07

树的定义

二叉树（Binary Tree）

二叉树的存储方式

链式存储

顺序存储

二叉树的遍历方式

LeetCode之路——144. 二叉树的前序遍历

分析

树的定义

树结构（Tree Structure）是一种分层的非线性数据结构，它由节点（Node）和边（Edge）组成，用于表示具有层次性关系的数据。树结构的一个关键特点是，每个节点可以有零个或多个子节点，但只有一个父节点（根节点除外）。根节点是树的顶层节点，它没有父节点，而叶子节点是没有子节点的节点。

以下是树结构的一些基本概念和术语：

节点（Node）： 树结构中的每个元素都被称为节点。节点可以包含数据或值，并可能有零个或多个子节点。
边（Edge）： 边是连接节点的线，它表示节点之间的关系。在树结构中，边代表从父节点到子节点的连接。
根节点（Root Node）： 根节点是树的顶层节点，它没有父节点，但可以有零个或多个子节点。
子节点（Child Node）： 子节点是位于某个节点下方的节点，即具有父节点的节点。
父节点（Parent Node）： 父节点是具有子节点的节点。一个节点可以同时作为多个子节点的父节点。
叶子节点（Leaf Node）： 叶子节点是没有子节点的节点，它们通常位于树的末端。
子树（Subtree）： 子树是从某个节点及其所有子节点构成的树，它是原始树的一部分。
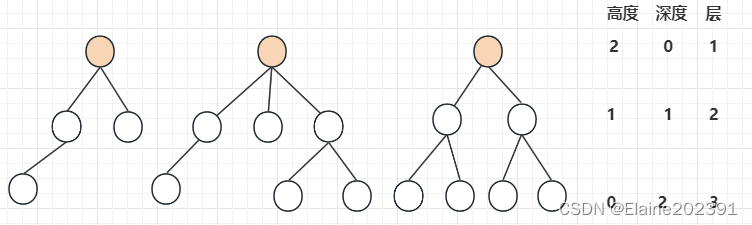
高度（Height）： 树的高度是从根节点到最深叶子节点的最长路径的长度。高度也称为深度。
层级（Level）： 树的层级是树中的层次结构，根节点位于第一层，其子节点位于第二层，以此类推。

话不多说，还是画图吧。

二叉树（Binary Tree）

二叉树是一种常见的树状数据结构，它的节点最多有两个子节点：左子节点和右子节点。根据二叉树的特性和结构，可以衍生出多种不同类型的二叉树。以下是一些常见的二叉树种类：

二叉查找树（Binary Search Tree，BST）： 二叉查找树是一种有序二叉树，其中每个节点的值都大于其左子树的所有节点的值，而小于其右子树的所有节点的值。这使得在二叉查找树中可以高效地进行搜索、插入和删除操作。
平衡二叉树（Balanced Binary Tree）： 平衡二叉树是一种特殊的二叉查找树，它保持树的高度相对平衡，从而保证了在最坏情况下的搜索效率为O(log n)。常见的平衡二叉树包括AVL树和红黑树。
满二叉树（Full Binary Tree）： 满二叉树是一种二叉树，除了叶子节点外，每个节点都有两个子节点。满二叉树的高度和节点数之间存在特定的关系，即高度为h的满二叉树有2^h - 1个节点。
完全二叉树（Complete Binary Tree）： 完全二叉树是一种二叉树，除了最后一层，其他层都是满的，最后一层从左到右填充节点。完全二叉树通常用于堆数据结构的实现。
二叉堆（Binary Heap）： 二叉堆是一种特殊的完全二叉树，它可以分为最小堆和最大堆两种类型。最小堆中，每个节点的值小于或等于其子节点的值；最大堆中，每个节点的值大于或等于其子节点的值。二叉堆常用于实现优先队列。
线索二叉树（Threaded Binary Tree）： 线索二叉树是一种特殊的二叉树，它添加了指向前驱和后继节点的线索，以支持更高效的中序遍历。
自平衡二叉树（Self-Balancing Binary Tree）： 这是一类平衡二叉树，包括AVL树、红黑树等，它们通过自动调整树的结构来保持平衡，以确保高效的插入、删除和搜索操作。

二叉树的存储方式

想要存储一棵二叉树，我们有两种方式，链式存储和顺序存储。

链式存储

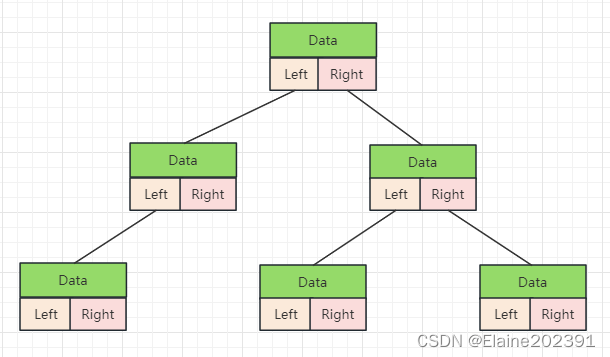
在链式存储中，二叉树的每个节点都包含数据、左子节点引用和右子节点引用。这种存储方式非常灵活，可以表示各种二叉树结构。

class TreeNode {
    int data;
    TreeNode left;
    TreeNode right;

    public TreeNode(int data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

// 创建一颗简单的二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);

顺序存储

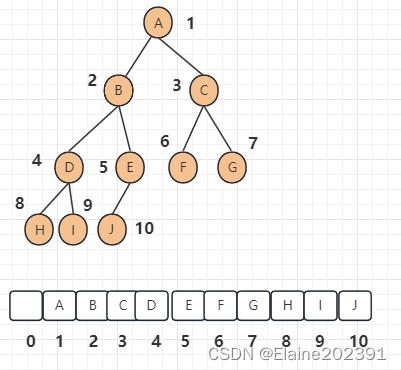
在数组存储中，二叉树的节点按照特定顺序存储在数组中，通常使用数组的索引来表示节点之间的关系。这种方式可以节省内存，但通常要求二叉树是完全二叉树。

如果节点X存储在数组中下标为i的位置，下标为2 * i 的位置存储的就是左子节点，下标为2 * i + 1的位置存储的就是右子节点。反过来，下标为i/2的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为1的位置），这样就可以通过下标计算，把整棵树都串起来。

class TreeNode {
    int data;

    public TreeNode(int data) {
        this.data = data;
    }
}

// 使用数组存储二叉树节点
TreeNode[] treeArray = new TreeNode[7];
treeArray[0] = new TreeNode(1);
treeArray[1] = new TreeNode(2);
treeArray[2] = new TreeNode(3);
treeArray[3] = new TreeNode(4);
treeArray[4] = new TreeNode(5);
treeArray[5] = new TreeNode(6);
treeArray[6] = new TreeNode(7);

// 使用数组索引表示节点关系
// 根节点的左子节点在索引1，右子节点在索引2
// 节点2的左子节点在索引3，右子节点在索引4
// 节点3的左子节点在索引5，右子节点在索引6

二叉树的遍历方式

经典的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。左节点永远先于右节点，什么顺序决定节点本身打印的位置。

前序遍历是指，对于树中的任意节点来说，先打印节点，然后再打印它的左子树，最后打印它的右子树。
中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它，最后打印它的右子树。
后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印它本身。

LeetCode之路——144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

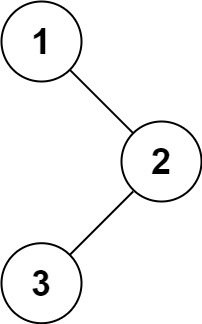
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

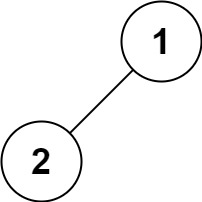
输入：root = [1,2]
输出：[1,2]

示例 5：

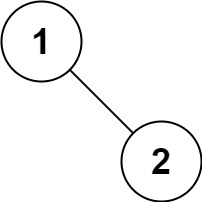
输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

分析

二叉树的递归求前序排列。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}