代码随想录算法训练营第二十八天 | LeetCode 491. 递增子序列、46. 全排列、47. 全排列 II

文章链接：递增子序列全排列全排列II

视频链接：递增子序列全排列全排列II

1. LeetCode 491. 递增子序列

1.1 思路

1.2 代码

2. LeetCode 46. 全排列

2.1 思路

2.2 代码

3. LeetCode 47. 全排列 II

3.1 思路

3.2 代码

1. LeetCode 491. 递增子序列

1.1 思路

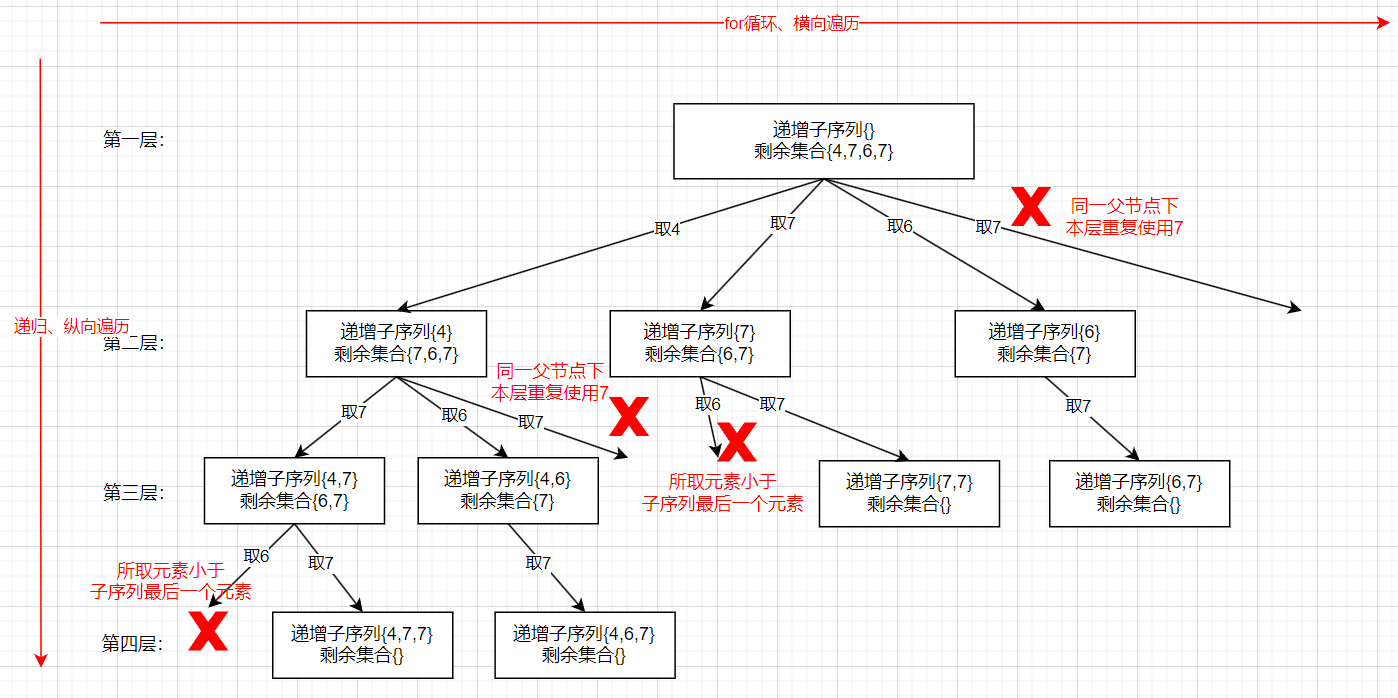
这题和90. 子集 II很像，但是又有点不同，相同的是都是求子集并且是有重复元素的，并要求不能有重复组合，不同的是这题我们不可以给数组排序，因为要求的是自增子序列，自增就是要按照题目的顺序，并且元素个数是要>=2 的
而我们用回溯算法去求难免会有重复的元素，因此需要去重，而去重的逻辑又不能与40. 组合总和 II和90. 子集 II相同，因为不能排序。这题属于回溯算法和深搜都对，本质是差不多的，所有回溯都是深搜
与之前一样，还是树层去重，树枝上数值是可以取数值相同的元素的，树层上是不可以的。树枝上允许出现 [4,7,7] 这种情况，但树层上如果第二次取相同数值的元素其实在第一次取了之后往下递归的过程在树枝上已经取过第二个相同的元素了，因此要树层去重
这里收集结果的地方其实也是树上的节点，只是对结果里的元素数量有要求，要>=2 个，因此收集结果的地方依然是在回溯函数的首行，只是要加个条件，里面的元素要>=2
综上我们要去重的部分其实主要就是两部分，第一是这个树层上重复出现的元素，第二是该元素比子序列的最后一个元素小的情况
定义两个全局变量，result、path
回溯函数的参数和返回值：返回值 void，参数 nums，startIndex 控制剩余集合的起始位置
终止条件：startIndex>=nums.length
单层搜索的逻辑：进入递归就收集结果，因为每个节点都是我们的结果，但是本题需要判断一下，与元素个数要>=2，把 path 加入到 result 中
要先定义个 HashSet set，就是做树层去重的，我们怎么知道同层前面取过了某个元素接下来就不能取了呢？就用 set 记录一下，for(int i=startIndex；i<nums.length；i++)，for循环每取一个就放入到 set 里，然后 for循环里判断如果要取的这个数已经在 set 里了就跳过此次循环。然后我们在取数时如果取的数比子序列最后一个元素小的话就不取，即 if( !path.isEmpty() && nums[i]<path.get(path.size()-1 || set.contains(nums[i]) )continue，这里的意思就是如果取的这个数比自序列最后一个元素小或者同一层已经取过这个数了就跳过，这里要加 !path.isEmpty() 因为集合为空会报异常。这里为什么是 continue 是因为这个元素不可以取了，下一个可能是能取的。
然后就是取数的过程，set.add(nums[i])，path.add(nums[i])。然后是递归 backtracking(nums, i+1)，然后是回溯的过程 path.remove(path.size()-1)。这里为什么不需要把 set 也回溯呢？因为这个 set 只是记录同一层里是否取过某个数，而进入递归时是新创建一个 set，再重新记录同一层是否取过某个数，set 的作用就是记录当前这层递归的元素别取重复了

1.2 代码

//
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backTracking(nums, 0);
        return result;
    }
    private void backTracking(int[] nums, int startIndex){
        if(path.size() >= 2)
                result.add(new ArrayList<>(path));            
        HashSet<Integer> hs = new HashSet<>();
        for(int i = startIndex; i < nums.length; i++){
            if(!path.isEmpty() && path.get(path.size() -1 ) > nums[i] || hs.contains(nums[i]))
                continue;
            hs.add(nums[i]);
            path.add(nums[i]);
            backTracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

2. LeetCode 46. 全排列

2.1 思路

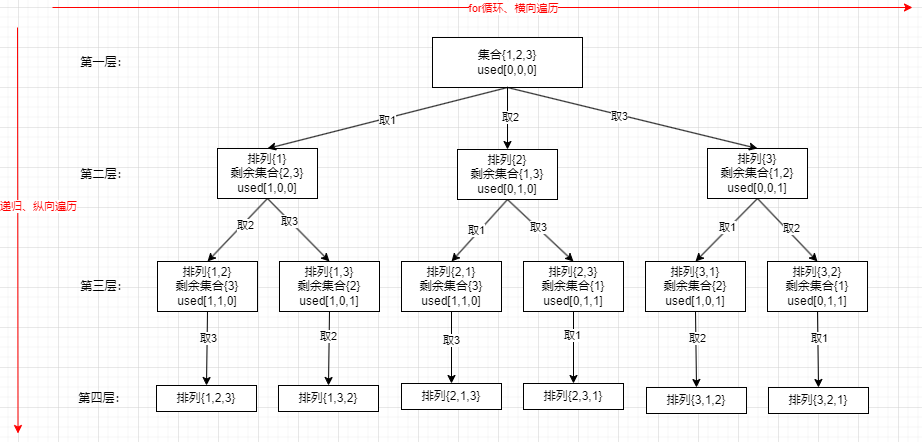
这题没有重复元素，因此不用考虑去重。这题是排列，需要清除与组合的区别。
这题需要用个 used 数组，之前都是用 used 来去重的，这里不需要去重为什么也用呢？这里是用 used 数组是标记哪个元素使用过了，我们求排列相同元素不能重复使用，和之前的去重逻辑是不一样的。做组合类问题时都是用 startIndex 来避免重复取同一个元素和出现 [1,2][2,1] 这种情况。
这题的结果都是在叶子节点上的，树的深度就是由集合的大小长度来控制的，因为最后取的排列就是和集合一样大的
定义三个全局变量，result、path、used 数组标记哪个元素已经使用过
回溯函数的参数和返回值：返回值 void，参数 nums
终止条件：当 nums.length==path.size()就把 path 加入到 result 中然后 return
单层搜索的逻辑：for(int i=0; i<nums.length; i++)这里为什么从 0 开始？因为之前用 startIndex 控制是为了避免重复，比如出现[1,2][2,1] 这种情况，而现在求排列 [1,2][2,1] 都是我们要的结果，因此每次取数都要从头开始，唯一要跳过的情况就是这一层取过这个数了，下一层就别取这个数了，也就是用 used 数组控制的。if(used[i]==true)就 continue，因为是 true 说明上一层用过了，就跳过此次循环。然后就是取数的过程，used[i]=true ，path.add(nums[i])。然后就是下一层递归了，backtracking(nums)。然后就是回溯，就是 used[i]=false，path.removeLast()

2.2 代码

//
class Solution {

    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++){
            if (used[i]){
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

3. LeetCode 47. 全排列 II

3.1 思路

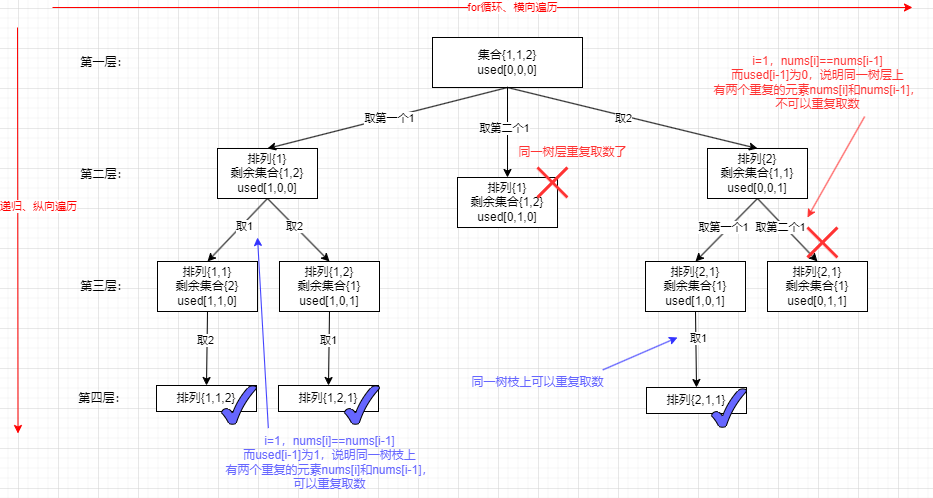
这题和46. 全排列的区别就是这题有重复元素，这样就会导致出现相同的排列不如两个{1,1,2}，因此要去重（注意这里去重需要先对题目的数组排序，因为要让相同的元素挨在一起）。同时这里也需要 used 数组标记哪些元素是否使用过，避免出现了使用两次同一个元素
依然是从树层去重和树枝去重的角度看。同一树层上，前面取过 1 后面就不能取 1 了，因为剩余集合是相同的，再取一次就会得到相同的排列，就重复了。而在同一树枝上上面取过 1 了，下面还可以取 1，这里没有重复取 1，上面取的是第一个 1 下面取的是第二个 1，这里是两个元素，排列里可以出现比如{1,1,2}这样子可以出现两个数值相同的元素。而结果是在叶子节点上，我们要砍去的分支都是在树层上如果和前面的树枝相同就要砍掉
定义三个全局变量，result、path、used 数组标记哪个元素已经使用过
回溯参数的参数和返回值：返回值 void，参数 nums
终止条件：当 path.size()==nums.length 就把 path 加入到 result 中然后 return
单层搜索的逻辑：for(int i=0; i<nums.length; i++)这里为什么从 0 开始？因为之前用 startIndex 控制是为了避免重复，比如出现[1,2][2,1] 这种情况，而现在求排列 [1,2][2,1] 都是我们要的结果，因此每次取数都要从头开始。而取数时有些不能取的，（i>0&&nums[i-1]==nums[i]&&used[i-1]==false）i>0 避免数组越界，然后树层上遇到相同元素就砍掉后面的分支，如果知道是树层而不是树枝呢？used[i-1]=false 就是树层，true 就是树枝，因为是回溯过来往树层右边取的。如果这个括号的条件为 true 就 continue 跳过此次循环，就是继续往树层右边搜索
然后是挨个取数的逻辑，取数时 if(used[i]==true)就 continue，这个情况就是排列里不能取同一个数的逻辑。然后就继续取数，used[i]=true，path.add(nums[i])，然后递归函数，然后回溯 used[i]=false，path.removeLast()

3.2 代码

//
class Solution {
    //存放结果
    List<List<Integer>> result = new ArrayList<>();
    //暂存结果
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        Arrays.sort(nums);
        backTrack(nums, used);
        return result;
    }

    private void backTrack(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
            // 如果同⼀树层nums[i - 1]使⽤过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树⽀nums[i]没使⽤过开始处理
            if (used[i] == false) {
                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
                path.add(nums[i]);
                backTrack(nums, used);
                path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
                used[i] = false;//回溯
            }
        }
    }
}