阶跃测试
只要是连续时间系统,无论是传递函数还是连续状态空间形式的模型,直接可以用**step()**做阶跃测试;但是对于离散系统而言,不能用step()函数,可以自行编写代码,如下。
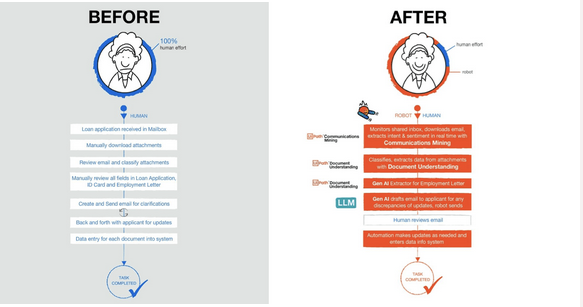
1、离散系统:x(k+1)=Ax(k)+Bu(k)
离散系统阶跃响应不能用step()函数,可以自行编写
close all;
clear all;
A=[1.1 2;0 0.95];B=[0;0.079];
total = 100;
x = zeros(2,total+1);
u = zeros(1,total);
u(1) = 1;
t = zeros(1,total);
for i=1:total
t(i) = i-1;
x(:,i+1) = A*x(:,i) + B*u(:,i);
end
figure(1);
subplot(3,1,1);
plot(t,x(1,1:total));
ylabel('x1')
hold on;
grid on;
subplot(3,1,2);
plot(t,x(2,1:total));
ylabel('x2')
hold on;
grid on;
subplot(3,1,3);
plot(t,u(1:total));
ylabel('u')
hold on;
grid on;

可见系统自身不稳定,因为离散系统的特征值有在单位圆外,如下

2、连续系统:x’=Ax+Bu或y=G(s)u
一个是连续状态空间模型,一个是传递函数模型
2.1 传递函数形式:
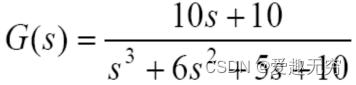
MATLAB里写成传函形式,并做阶跃测试**step()**函数

2.2 化成连续状态空间形式

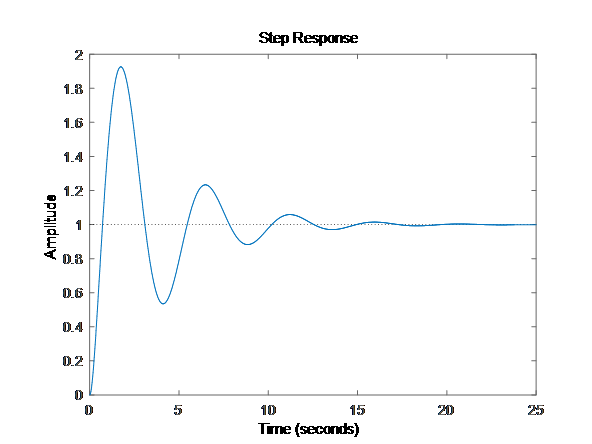
再做阶跃
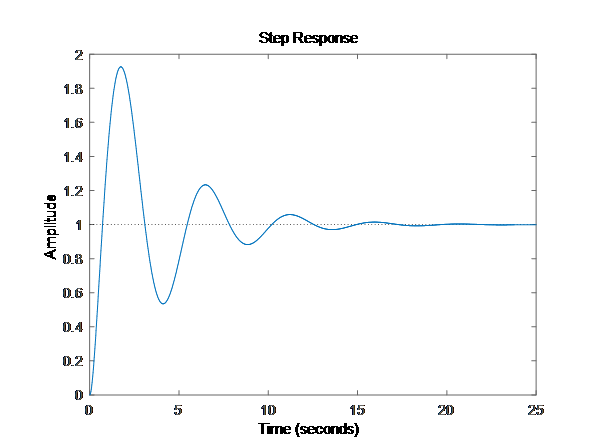
不管是传函,还是连续状态空间,step()测试结果相同,说明系统稳定,因为状态矩阵特征值都<0;
eig(A)
ans =
-5.4178 + 0.0000i
-0.2911 + 1.3270i
-0.2911 - 1.3270i
2.3 连续状态空间形式化成离散状态空间形式
(1)对传递函数进行离散

得到的是离散时间传递函数,z变换
(2)对连续状态空间模型进行离散

得到的是离散状态空间模型
(3)对离散状态空间模型做阶跃测试
离散系统阶跃响应不能用step()函数,可以自行编写,就是本文第1节,下面继续写一遍:
A = [0.5307 -0.2069 -0.1864;0.1491 0.978 -0.02058;0.01647 0.1985 0.9986];B = [0.1491;0.01647;0.001152];C = [0 2.5 1.25];%得到的离散状态空间模型
total = 100;
x = zeros(3,total+1);
u = zeros(1,total);
u(1) = 1;
y = zeros(1,total);
t = zeros(1,total);
for i=1:total
t(i) = i-1;
x(:,i+1) = A*x(:,i) + B*u(:,i);
y(:,i+1) = C*x(:,i+1);
end
figure(1);
subplot(3,1,1);
plot(t,x(1,1:total));
ylabel('x1')
hold on;
grid on;
subplot(3,1,2);
plot(t,x(2,1:total));
ylabel('x2')
hold on;
grid on;
subplot(3,1,3);
plot(t,x(3,1:total));
ylabel('x3')
hold on;
grid on;
figure(2)
subplot(2,1,1);
plot(t,u(1:total));
ylabel('u')
hold on;
grid on;
subplot(2,1,2);
plot(t,y(1:total));
ylabel('y')
hold on;
grid on;
图形如下:
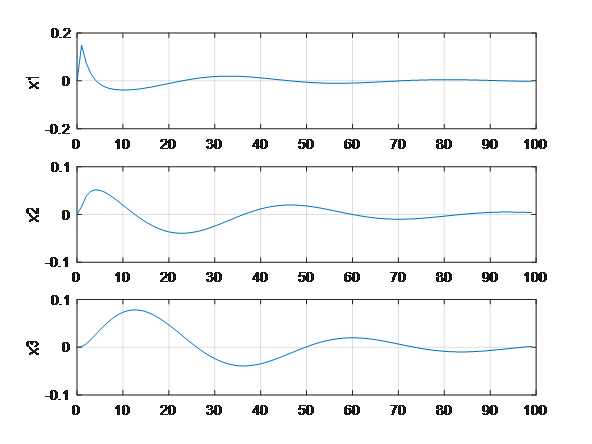
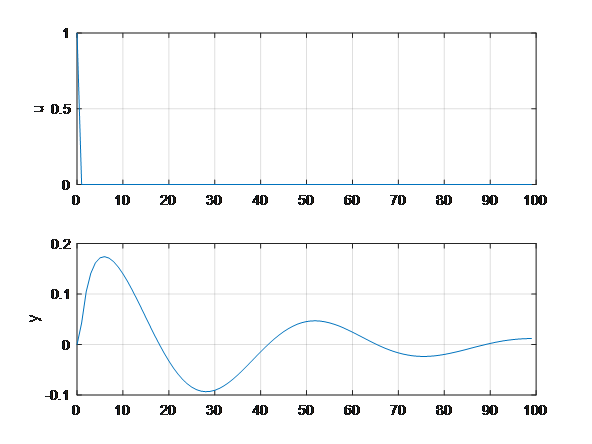
化成离散系统后,仍然稳定。