ls：

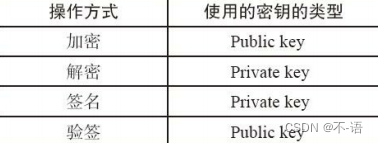
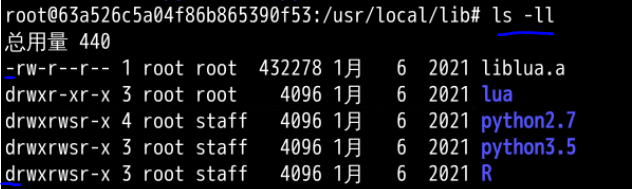
如何区分一个文件类型是 文件夹 还是 普通文件：
“-” 类型 表示是 普通文件
“d” 类型 表示是 文件夹

cd：

cd -

返回进入此目录前所在的目录

cd ~

如果是root用户，相当于 cd /root；如果是普通用户，相当于 cd /home/当前用户名

cat：

cat本意是拼接多个文件后输出到屏幕上，但是大部分使用时都是直接输出某一个文件，不需要拼接

cat [file] -n	// --number, number all output lines, 给输出的内容打上行号

head：

cat命令是查看一个文件的完整内容，但有事文件过大，cat查看不方便，则可以使用head命令。

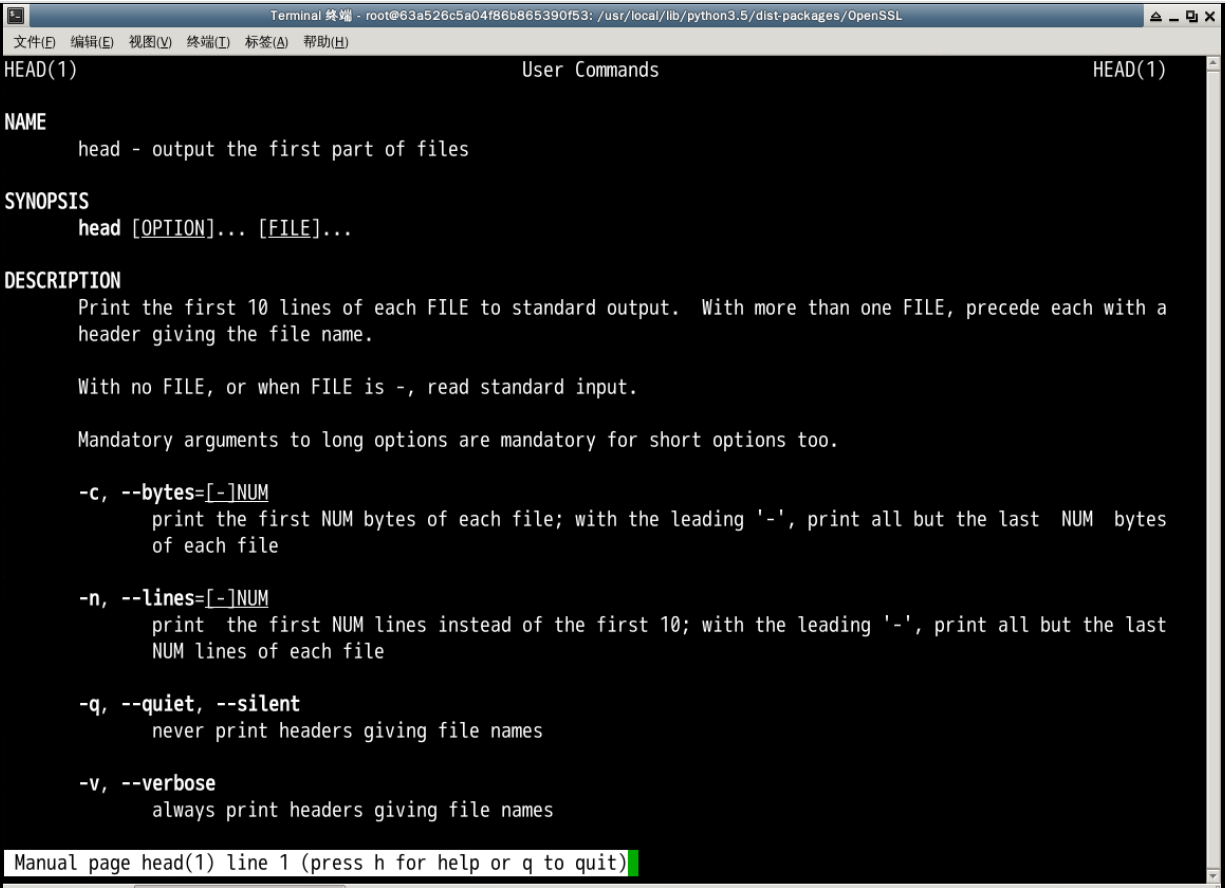
head命令用于查看一个文件的“开头部分”，默认是文件的前10行，如果需要查看不同的行数，则使用 -n 选项：

head [file] -n [number]

tail：

相对于head命令用于查看文件的开头部分，Linux中的tail命令则是用于查看文件的尾部，同样默认查看倒数10行，如果需要修改行数则使用 -n 选项：

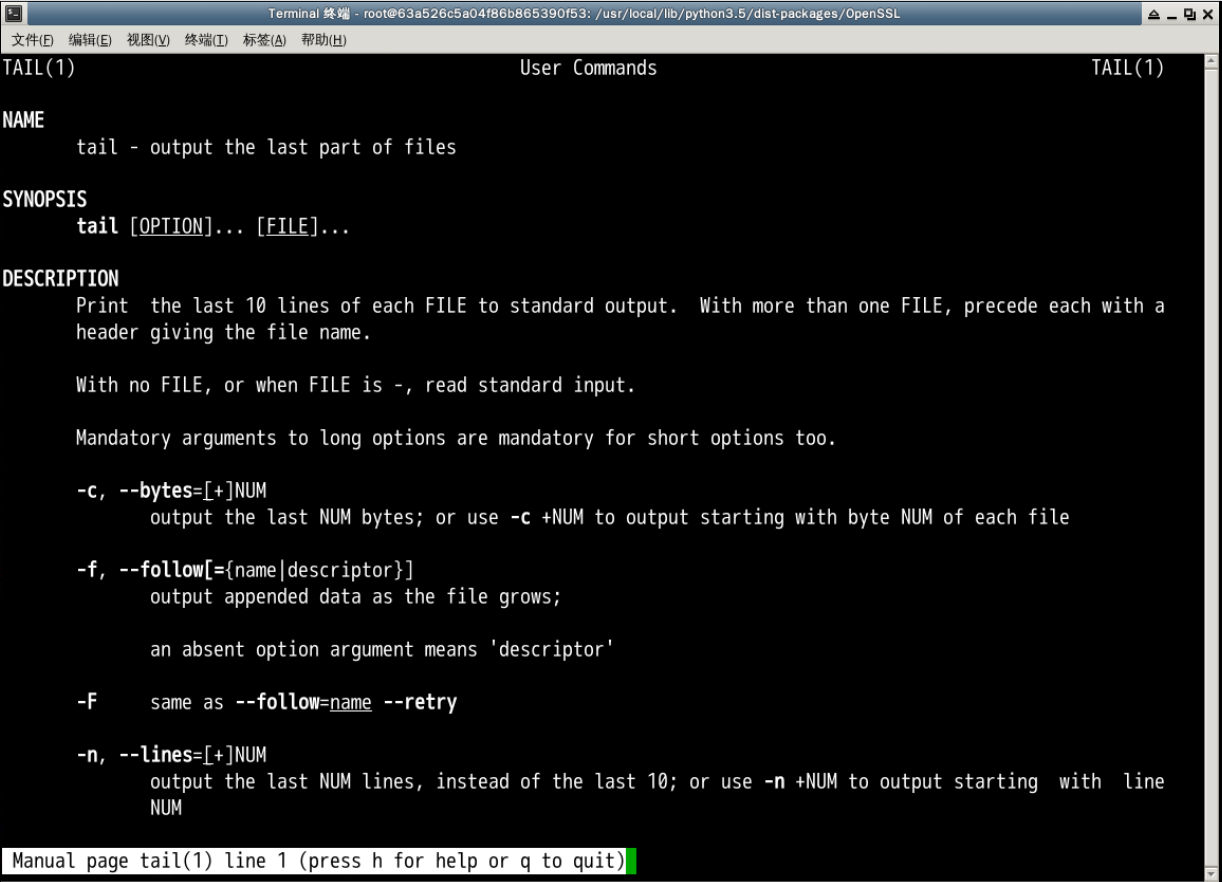
tail [finename] -n [number]

more：

more命令用于从前向后滚动查看文档内容，但是只能向下，不能向上，Enter键翻一行，空格键翻一页（适配屏幕大小）。

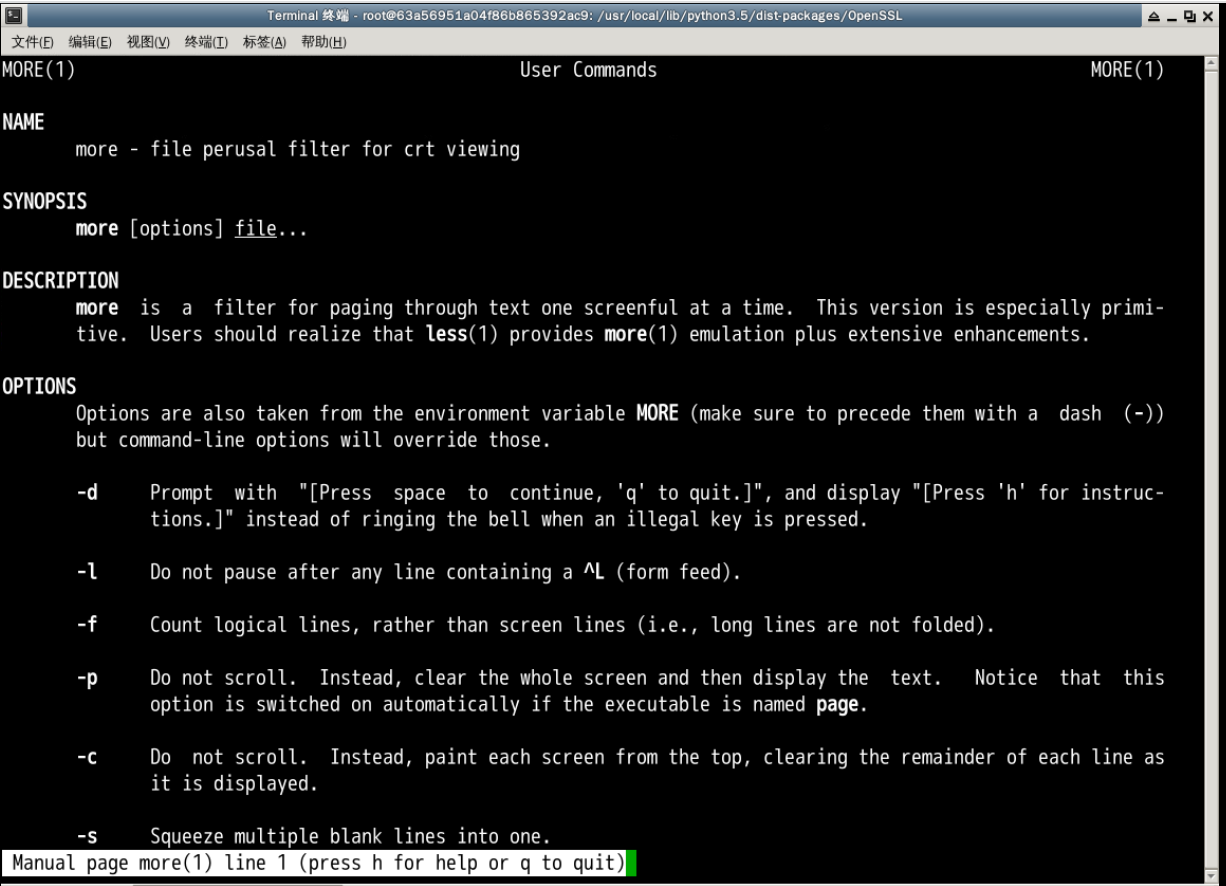
less：

less命令同样是用于查看 文档，但是比more支持更多的功能：不必从头开始、支持向上和向下等。

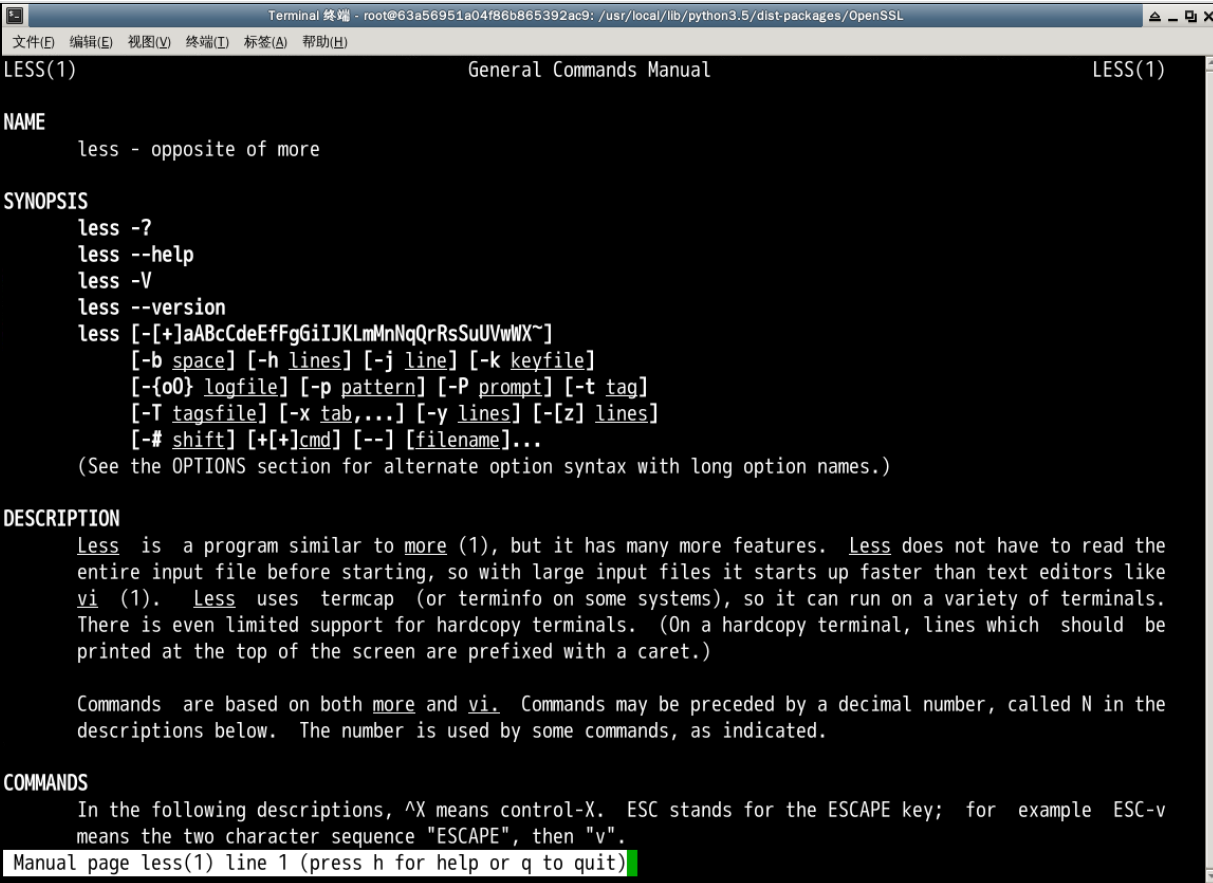
Shell编程之for循环：

语法格式：

for [变量名] in [取值列表]
do
	[命令]
done

例如：

for i in Week??
do
echo ${i}
done

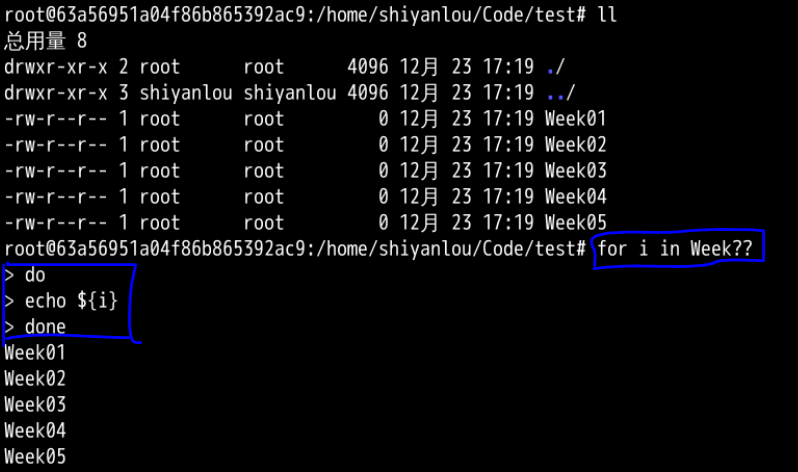
替换操作：把所有文件名中的Week替换为Chapter：

?? 表示模糊匹配两个字符位置
# 表示删除掉这串内容