题目：

93. 递归实现组合型枚举 - AcWing题库 

 

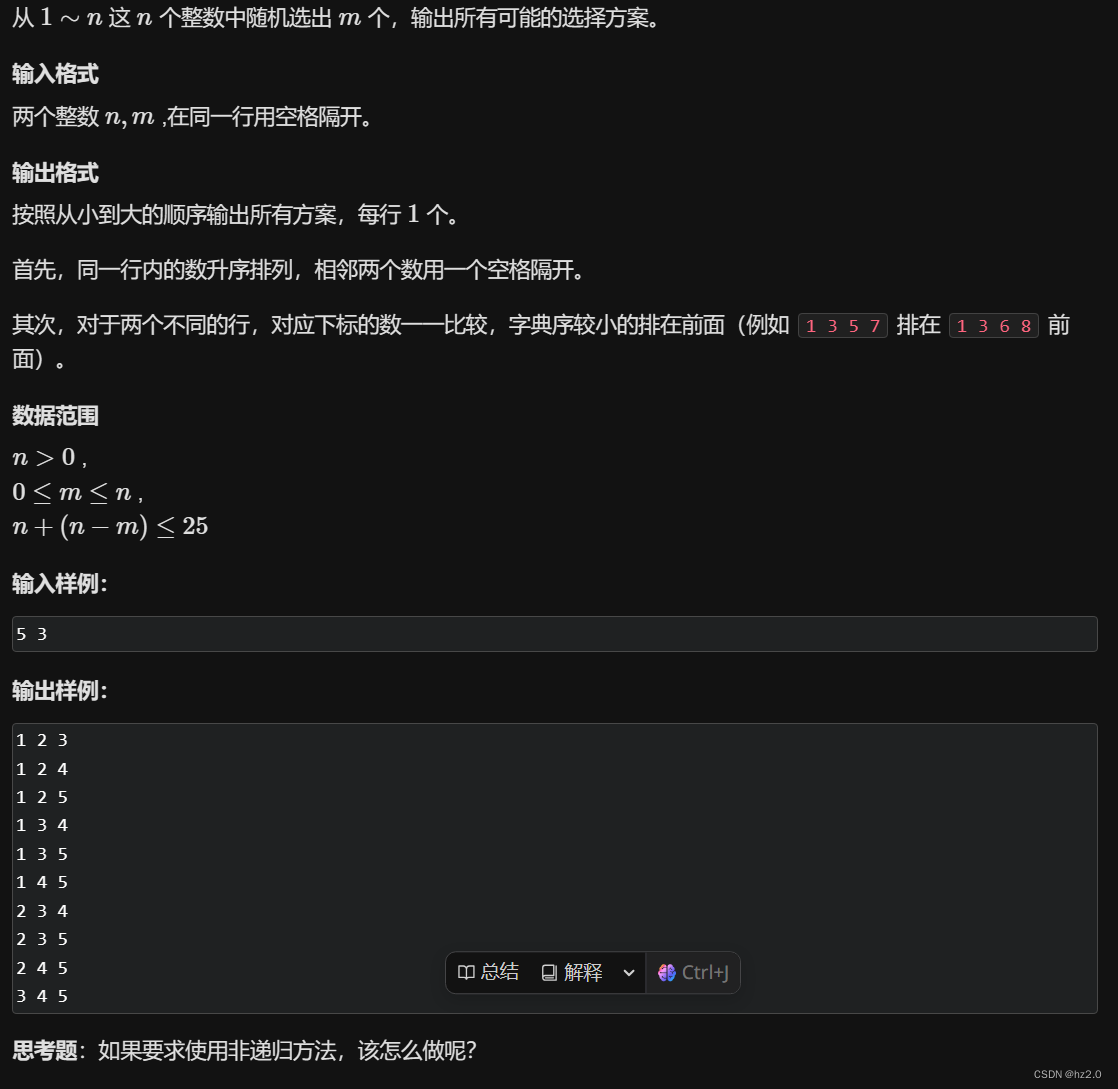
思路： 

 1.从n个数中选择m个数，问有多少种选法。---->抽象为有m个坑位（设置kenway[N]表示），其中填入编号为1~n的萝卜，问有几种填法。这里我们可以采用递归搜索树的方法枚举。u表示当前搜索到的坑位。

2.注意：因为是问有多少种组合而非排列，故不用考虑顺序（即12与21属于一种）。为防止搜索时在坑位已经记录了12的情况下再次记录21导致重复，我们要求坑位kenway[i]上的数字依次递增-->我们需要再定义一个start表示每个坑位kenway[i]最小可以取的值。

3.优化：不难发现，例如萝卜编号为1~5（n=5），坑位数量为3（m=3）。当第一个坑位填入编号为4的萝卜时，为满足后面2个坑位递增，第二个坑位只能选择5，那么第三个坑位就没有可选择的萝卜了，故kenway[1]填入4时的这条递归搜索树分支没有继续向下搜索的必要了，因而此处我们可以实行剪枝操作。（当u-1+n-start+1<m时，直接return掉这条分支）

代码：

//用dfs深度优先搜索（一条路走到黑才转头回到上一步）
#include<cstdio>
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
const int N = 30;
int kenway[N];
int n, m;
void dfs(int u, int start)
{
	if (u + n - start < m)return;//递归搜索树剪枝
	if (u == m + 1) {//表示坑位已经暴格了-->输出并结束这条搜索线
		for (int i = 1; i <= m; i++)printf("%d ", kenway[i]);
		puts("");
		return;
	}

	for (int i = start; i <= n; i++) {
		kenway[u] = i;//给当前坑位赋值（第一个坑位可以赋值从1到n）
		dfs(u + 1, i + 1);//(在前一个坑位为i的基础上)判断下一个坑位
		kenway[u] = 0;//恢复现场
	}
	return;
}

int main()
{
	cin >> n >> m;
	dfs(1, 1);//从第一个坑位开始放数，从1开始放
}