最近有朋友在研究Halcon中gen_gabor的函数，和我探讨，因为我之前也没有怎么去关注这个函数，因此，前前后后大概也折腾了有一个星期去模拟实现这个东西，虽然最终没有实现这个函数，但是也是有所收获，这里做一点总结，也算是最这个函数有个完美的收尾吧。

　　1、Gabor滤波器

　　首先总是度娘出场，关键词Gabor滤波器，一大堆东西出来了，里面最多的肯定是关于OpenCv的getGaborKernel函数，这个函数的具体代码如下：

/*
 Gabor filters and such. To be greatly extended to have full texture analysis.
 For the formulas and the explanation of the parameters see:
 http://en.wikipedia.org/wiki/Gabor_filter
*/
cv::Mat cv::getGaborKernel( Size ksize, double sigma, double theta,
                            double lambd, double gamma, double psi, int ktype )
{
    double sigma_x = sigma;
    double sigma_y = sigma/gamma;
    int nstds = 3;
    int xmin, xmax, ymin, ymax;
    double c = cos(theta), s = sin(theta);
    if( ksize.width > 0 )
        xmax = ksize.width/2;
    else
        xmax = cvRound(std::max(fabs(nstds*sigma_x*c), fabs(nstds*sigma_y*s)));

    if( ksize.height > 0 )
        ymax = ksize.height/2;
    else
        ymax = cvRound(std::max(fabs(nstds*sigma_x*s), fabs(nstds*sigma_y*c)));

    xmin = -xmax;
    ymin = -ymax;
    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(ymax - ymin + 1, xmax - xmin + 1, ktype);
    double scale = 1;
    double ex = -0.5/(sigma_x*sigma_x);
    double ey = -0.5/(sigma_y*sigma_y);
    double cscale = CV_PI*2/lambd;
    for( int y = ymin; y <= ymax; y++ )
        for( int x = xmin; x <= xmax; x++ )
        {
            double xr = x*c + y*s;
            double yr = -x*s + y*c;

            double v = scale*std::exp(ex*xr*xr + ey*yr*yr)*cos(cscale*xr + psi);
            if( ktype == CV_32F )
                kernel.at<float>(ymax - y, xmax - x) = (float)v;
            else
                kernel.at<double>(ymax - y, xmax - x) = v;
        }
    return kernel;
}

　　可以快速看出，这段代码仅仅是根据一些参数计算出一个卷积核，具体的公式我也没怎么关注，里面有个nstds 这个常量为3，这个只在用户输入的ksize尺寸为0的时候需要用到，感觉是和高斯核函数在半径大于3*Sigma后其对结果的贡献就可以忽略不计有关。 

　　这个函数生成的卷积核的形状和参数之间的关系，很多文章都有探讨，这个不是本文的重点，比如下面这个链接：https://blog.csdn.net/Wslsdx/article/details/110728050

　　基本上，在空域他的形状就是一些有间隔的白色过度条，在频域，则基本为两处白色亮点，如下图所示：

      

 　　　 

　　　　　　卷积核空域图形化　　　　　　　　　　　　　　　对应的频域图

　　通常，CV的getGaborKernel函数都要配合Filter2D函数进行卷积得到想要的结果。 

　　网络上一个有意思的视觉效果方面的算法在OpenCV获取和使用Gabor滤波器 - 知乎有提到，可以用这个滤波器来做一些特效。

static std::vector<cv::Mat> build_filters()
{
    std::vector<cv::Mat> filters;
    const int ksize = 31;
    const double sigma = 4.0;
    const double lambd = 10.0;
    const double gamma = 0.5;
    const double psi = 0;
    // 此处创建16个滤波器， 只有 getGaborkernel 的第三个参数 theta 不同
    for (int i = 0; i < 16; i++)
    {
        double theta = CV_PI * i / 16;
        cv::Mat kernel = cv::getGaborKernel(cv::Size(ksize, ksize), sigma, theta, lambd, gamma, psi, CV_32F);
        kernel /= 1.5 * cv::sum(kernel)[0];
        filters.emplace_back(kernel);
    }
    return filters;
}
cv::Mat process(const cv::Mat& src, std::vector<cv::Mat>& filters)
{
    cv::Mat accum = cv::Mat::zeros(src.size(), src.type());
    for (cv::Mat kernel: filters)
    {
        cv::Mat fimg;
        AutoTimer timer("filter2D");
        cv::filter2D(src, fimg, CV_8UC3, kernel); // 这里是耗时的瓶颈
        AutoTimer timer("getmax");
        accum = cv::max(accum, fimg);
    }
    return accum;
}
int main()
{
    cv::Mat src = cv::imread(image_path);
    std::vector<cv::Mat> filters = build_filters();
    cv::Mat res = process(src, filters);
}

 　　

 、

　　这里用了16个滤波器组合求最大值，得到了一种特征线条凸出的效果。 

　　当然，OpenCv的这个滤波器在一些特征识别方面也有着很大的作用，比如斑马线识别等等。

　　但是，测试发现这个滤波器对参数的配置极其敏感，同一个参数，一般两个值如果只相差一点点，一般出来的效果不会有太大的区别，但是这个函数，确可能会出现极大的差异。比如波长这个参数，当为0.4和0.5的结果大相径庭。  

　    

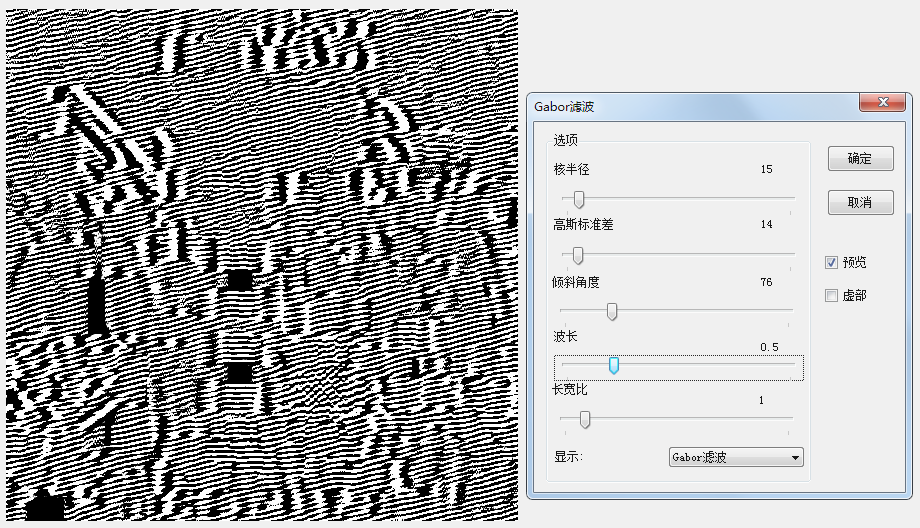
　　　　　　　　　　　　　　　　波长为0.4时的结果　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　波长为0.5时的结果

　　仔细的分析这个问题，我们会发现，这个还是由于当参数改变时，这个滤波器的权重会出现波动，一般这些卷积核都需要归一化或做相关处理，当波长为0.5时，我们会发现归一化时，所有滤波器的和可能为负数或者很小的数，而为0.4时则较为正常。因此，出现了参数改变一点点，结果改变一大串的问题。

　　再稍微撤远一点，当我自己实现这个函数时，我们会发现他的主要耗时还是Filter2D函数，关于这个函数，OpenCV内部是做了优化的，他会根据硬件的支持情况使用opencl/ipp等加速资源实现，速度是相当的快，而且也会对核的大小做判断，很小的核不会使用FFT。  我这里直接使用FFT做的实现，虽然我在进行FFT卷积时做了很多优化，比如拆解为多个256*256的FFT， 比如充分利用虚部的数据等等，结果还是干不过Opencv的速度。

　　二、LogGabor滤波器

　　拿OpenCv的Gabor滤波器和Halcon的gen_gabor相比，发现他们根本不是一回事，gen_gabor直接生成了频域的数据，而不是生成了卷积核。关于这个算子，我们发现halcon里的描述也不是特别的清晰，这有点不太像他的风格。

　　百度搜索gen_gabor我们能发现的99%的资料都是halcon帮助文档的英文原版或者是相关翻译，基本没有对其进行原理进行描述。可能也是因为这个算子不是很常用的原因吧。

　　在搜索Gabor滤波器时，也看到了一些文章讲LogGabor滤波器，其中有一篇文章有提到 Log-Gabor函数并不能在空间域中得到表达式，滤波器的构造须在频域中进行，这个和gen_gabor的描述非常相似。后面我们对其参数进行了一些分析，基本可以确定halcon的gabor应该是类似于LogGabor滤波器之类的。

　　通过搜索LogGabor，我们得到了一下几个比较有用的参考链接和代码：

　　　Python OpenCV实现Log Gabor滤波器（由LGHD描述符扩展） 以及 Github中一篇 PhaseCongruency/gaborconvolve.m的matlab代码

　　还有一个非常有用的图片：

　             　

　　通过阅读这几篇文章及其配套的代码，我们发现这个频域的滤波器可由Log-Radial Gaussian和Angular Gaussian组合而成，在Python那篇文章中，则有这更为明确的公式：

　　原文描述如下：

　　　　　　一个二维的L-Gaborj波器可以分解为径向滤波器和角度滤波器两部分，对应极坐标公式为:

　　　　　　　　　　

　　　　　　完整的Log-Gabor滤波器由这两部分相乘得到:

　　　　　　　　　　　　

　　这个公式也和上面的图片能完全对应。

　　在代码实现上，我发现无论是Python的代码还是matlab的代码其实都是一个版本的，他们在计算有关的过程中都有一个lowpass的过程，我不清楚那个是目的是啥，也不知道哪里的参数来源依据是什么，但是我感觉他们不应该是我所需要的，我需要的就是上面两个公式，结合那些参考代码，我们对第一个公式（径向滤波器）的M代码实现如下：

WaveLength = 10;
SigmaR = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
radius = sqrt(x.^2 + y.^2);       
Frequency = 1.0 / WaveLength;                  % 频率等于波长的导数
logGabor = exp((-(log(radius / Frequency)).^2) / (2 * SigmaR * SigmaR));  % log gabor函数的传递函数表达式
imshow(logGabor,[])

　　对第二个公式的实现代码如下：

Angle = 45 / 180 *3.1415926;
SigmaA = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
theta = atan2(-y,x);              
sintheta = sin(theta);
costheta = cos(theta);
ds = sintheta * cos(Angle) - costheta * sin(Angle);    
dc = costheta * cos(Angle) + sintheta * sin(Angle);     
dtheta = atan2(abs(ds),abs(dc));                           
spread = exp((-dtheta.^2) / (2 * SigmaA * SigmaA));      
imshow(spread,[])

　　当将两者组合起来后，即产生如下的代码：

WaveLength = 10;
SigmaR = 0.4;
Angle = 45 / 180 *3.1415926;
SigmaA = 0.4;
cols = 500, rows=500;
[x,y] = meshgrid( [-cols/2:(cols/2-1)]/cols,[-rows/2:(rows/2-1)]/rows);
radius = sqrt(x.^2 + y.^2);  
Frequency = 1.0 / WaveLength;                  % 频率等于波长的导数
logGabor = exp((-(log(radius / Frequency)).^2) / (2 * SigmaR * SigmaR));  % log gabor函数的传递函数表达式
theta = atan2(-y,x);              
sintheta = sin(theta);
costheta = cos(theta);
ds = sintheta * cos(Angle) - costheta * sin(Angle);    
dc = costheta * cos(Angle) + sintheta * sin(Angle);     
dtheta = atan2(abs(ds),abs(dc));                           
spread = exp((-dtheta.^2) / (2 * SigmaA * SigmaA));      
imshow(logGabor .* spread,[])

　　三段代码产生的图像依次如下所示：

 

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　WaveLength = 10，SigmaR = 0.4，Angle = 45 / 180 *3.1415926， SigmaA = 0.4;

　　通过改变参数可以获得不同的效果，比如，WaveLength = 5，SigmaR = 0.05，Angle = 30 / 180 *3.1415926， SigmaA = 0.3时的效果如下：

　

 

  

　　注意到，相比于原始的代码，我们在计算dtheta时，稍微做了修改，这是因为，频域的数据一般是要求堆成的，而原始的角向滤波器是非对称的，因此，我们改成了atan2(abs(ds),abs(dc));

　　这个生成的过程里有很多浮点的计算，而且有几个复杂度比较高的函数，因此，计算还是有所耗时的。 

　　我们来和halcon的gen_gabor的参数做下比较：

　　　　　　　　gen_gabor( : ImageFilter : Angle, Frequency, Bandwidth, Orientation, Norm, Mode, Width, Height : )

　　后面Norm, Mode, Width, Height 这四个参数不用管它，我们主要看看前面四个参数。 

　　注意到我们刚才的代码里也提供了四个可选的参数，即WaveLength，SigmaR，Angle， SigmaA，那他们之间有么有什么对应的关系呢。 

　　通过多次比较和测试，我们可以定性的确定如下联系：

　　1、gen_gabor里的Orientation和我的LogGabor里的Angle基本是一个意思，这个可以从Orientation的范围可以看到，就是个角度范围：

　　　　　Orientation (input_control) real → (real)
　　　　　　　　Angle of the principal orientation，Suggested values: 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.14

　   2、gen_gabor的Bandwidth和LogGabor的SigmaR的趋势基本是一致的。

       3、gen_gabor的Frequency和LogGabor的WaveLength的趋势基本是相反的，但是WaveLength本身就是Frenquency的倒数，都是会随着Frequency的变小，频域的有效部分想中心收缩。

       4、gen_gabor的Angle和LogGabor的SigmaA的趋势基本是相反的。

　　也就是说这4个参数基本上都存在一一对应的关系，只是说我们无法确认他们之间的绝对值之间的联系，毕竟halcon里也没有提供具体的计算式，只要稍微某个地方有些取值不同，就会造成不同的结果。 

　　由于loggabor提供的已经是频域的数据了，因此，后续的计算就比较简单了，因为频域的乘法就相当于于时域的卷积，因此，直接把某个图像的频域数据乘以这个LogGabor数据就可以了。

       但是，这就要求LogGabor的数据维度必须和图像是一样大小的，其实这个有个隐藏的问题，即边缘问题，因为卷积对于边缘一般来说是需要扩展的，否则会遇到一些小小意料之外的问题。 

　　做了一个简单的比较，当gen_gabor和LogGabor滤波器的可视化图基本类似时，大部分情况两者之间的效果似乎方向是一致的。 

  

    

　　　　　　　　　　　　halcon的gen_gabor可视化结果　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　对应的滤波器输出

  

  

　　　　　LogGabor参数　　　　　　　　　　　　　　　　　　　　　　　　　　　　LogGabor可视化结果　　　　　　　　　　　　　　　　　　　　　　　　　　　　对应的滤波器结果

　　上述结果的halcon代码如下所示：

read_image (Image, 'fabrik')
get_image_size (Image, Width, Height)
gen_gabor(Filter,10,0.1,50,1.57,'n','dc_center',Width, Height)
fft_generic(Image,ImageFFT,'to_freq',-1,'none','dc_center','complex')
convol_gabor(ImageFFT,Filter,Gabor,Hilbert)
fft_generic(Gabor,GaborInv,'from_freq',1,'none','dc_center','byte')

　　可以看出，两者的结果存在一定的相似性，从某个侧面说明我们的猜测具有一定的科学性。

　　三、速度优化

　　从上面的过程可以看到我们的LogGabor滤波器的生成有着较为复杂的计算公式，而且有多个函数调用，这些函数其实都是有着较为复杂的内部计算的，要进行优化，可以从多方面出发，第一个是用C语言处理吧，把一些公共的计算放到循环外部，把能优化掉的除法尽量改为乘法，还可以把那个exp的计算合并为一个，因为我们知道exp(a) * exp(b) = exp(a+b)，这样就可以减少一次exp计算了。

　　当然，我们还可以进行指令集优化，我们可以自定义_mm_atan2_ps, _mm_sincos_ps, _mm_exp_ps等等指令集函数（网络上可以找到的），他们可以接受成吨的输出。很爽，至少速度比C版本的提高3到4倍。

　　我们在计算频域相乘时，也可以适当的考虑扩大图像，让图像的尺寸变为那些更有利于做FFT变换的数据，比如4、5、8的倍数等等，这样，可以有效地提高FFT的运算速度，并且对结果只会造成轻微的影响。

　　关于这个算法目前就研究这么多吧，希望能造福有需要的人，也能造福自己。

　　此更新算法位于我的SSE Demo的如下目录：   Detection(检测相关）---》Gabor Filter(Gabor滤波)。

　　SSE Demo下载地址： https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar

　　如果想时刻关注本人的最新文章，也可关注公众号或者添加本人微信：  laviewpbt