一、背景介绍

随着相关技术的发展，图计算与分析系统在大量场景中得到应用。同时，为了解决图规模巨大等因素导致的性能下降问题，研究人员利用GPU这一新型计算硬件，设计了大量高效的图计算与分析解决方案。GPU提供的高并发计算能力和高带宽存储器件都为此提供了基础。

现存解决方案的一大突出问题在于，大部分方法的假设是图数据本身是静态的不变的。然而，这与许多应用场景的实际情况并不符合。在我们常见的诸如电商、社交网络等应用场景当中，图数据本身是不断变化的。例如，在电商场景中经常将用户的交易行为视作图数据来管理，通过运行图模式匹配等算法进行欺诈、刷单等行为的检测。而这些算法基于的数据会以每秒成千上万条记录的速度进行增加或删除。这一情况要求图计算与分析系统能够支持对动态图的数据管理（Dynamic Graph Management，下称DGM）。通过维护动态图数据结构，既要支持图数据本身的增删改，也要提供恰当的接口供下游查询使用，还要通过特定的优化使得其符合GPU硬件的特性。

具体而言，在GPU上进行DGM技术的设计有以下几个挑战。

第一，图数据的更新速度快。要求DGM解决方案能够充分利用GPU的高并发和高带宽能力，设计有效的数据存储结构和并发增删改查策略。

第二，下游的图计算和分析系统执行各种各样的访问和查询模式。因此，难以找到一种一体适用，放之四海而皆准的DGM解决方案，但我们能够通过横向比较和定性分析确定什么样的DGM解决方案更适合不同的访问模式。

第三，图数据本身的体量巨大，需要消耗大量的存储和计算资源。图数据本身还有分布不均匀的问题，使得并发执行时产生负载不均的问题。

第四，GPU硬件本身的特性在设计DGM解决方案时同样需要考虑。否则，系统性能可能还不如纯CPU环境下的解决方案。

二、相关概念的区分

为了更好地理解GPU上DGM问题这一概念，本章节本文对DGM相关的概念进行列举和描述。

DGM问题中对图的定义为,其中是图中点的集合，是图中边的集合。图中的点与边可能有一系列属性。例如，点可能有标签和点代表的实体的属性，边可能有标签和权重。

从图数据的表示方法角度看，现有的解决方法可以分为四类。

第一种是基于邻接矩阵（Adjacency Matrix）的表示方法。这种方法将图表示为一个的矩阵，其中第行第列的元素表示点和点之间的边。这种方法的好处是可以在常数时间内完成边的插入和删除操作，但是对点进行插入时的代价较大，而且容易导致存储的矩阵非常稀疏，浪费空间。

第二种是基于邻接表（Adjacency List）的表示方式。这种方法为每个点维护一个邻居列表（两个有边相连的点互为邻居），每个列表保存与这个点相连的所有点。这种方法的好处是在插入和删除边时，不同的点的邻居列表的修改可以互不干扰。

第三种是基于边列表（Edge List）的表示方式。这种方法将图中所有的边表示为一个点对，并将所有边连续存储或分段连续存储。这种方法的主要问题是会引入多余的空间消耗。

第四种是基于邻接数组（Adjacency Array）的表示方式。这种方法同样为每个点维护一个邻居列表，而不同之处在于这种表示方法将所有邻居列表连续存储。这种方法能够很大程度上减少空间消耗，在读取时能够减少随机访存带来的代价。

在现存的相关工作中，有两个较为相似的概念：流图（Streaming Graph）与动态图（Dynamic Graph）。这两个概念本质上都是指图数据会不断地被修改。类似的概念还有在线图（Online Graph）和时序图（Time-evolving Graph）。两个概念的主要区别在于开展相关研究时的侧重点略有不同。流图相关的研究中，更多地关注系统的实时性，即每一次修改时系统都要作出响应，图算法的执行和图数据的修改同时发生。因此，这些研究更关注近似的算法和增量的算法，并且考虑插入的边仅在一个时间窗口中留存。而动态图相关的研究中，边的更新通常以批（Batch）为单位，图算法的执行和图数据的更新交替执行。

另一个与DGM相关的概念为图数据库（Graph Database）或图存储引擎（Graph Storage Engine）。它们同样能够支持图数据的增删改查操作。实际上，从这个角度看，确实能够使用图数据库或图存储引擎来作为DGM的解决方案，但二者的应用场景略有不同。图数据库和图存储引擎更侧重事务处理（Transaction Process）和ACID支持。它们往往考虑支持的图数据中的点和边具有更丰富的属性，因此它们使用的底层索引和存储结构更加复杂，而DGM考虑支持的点和边属性通常很少，底层的数据结构也更轻量化以最大化处理的吞吐量。

另外还有两个经常与DGM混淆的概念。其一是流式图处理（Streaming Graph Processing）,这一概念实际是跟边中心式图计算（Edge-centric Processing）相同，是指将图数据视作一个数据流，遍历图数据中的边执行计算的计算框架。这与图数据是否修改无关。其二是时序图处理（Temporal Graph Processing），这一概念下图数据的确会进行修改，但是与DGM不同的是时序图处理中不仅要保存图数据的当前状态，还需要对其历史状态进行查询。

三、相关工作介绍

接下来本文将介绍两篇在GPU上给出DGM解决方案的代表性工作。

（一）FaimGraph: High Performance Management of Fully-Dynamic Graphs Under Tight Memory Constraints on the GPU

第一篇是来自奥地利格拉茨大学的研究人员发表在SC2018的文章，题目为《faimGraph: High Performance Management of Fully-Dynamic Graphs Under Tight Memory Constraints on the GPU》。此文章的主要贡献为提出了faimgraph这一面向大规模动态图的DGM解决方案。本文作者为faimgraph通过一种针对图数据特点的基于空闲队列的方法，设计了高效的存储空间重用机制。

该研究的主要动机是，作者通过分析现有系统的不足，发现在GPU上DGM解决方案的访存代价对整体性能的影响更加显著。具体地说，下游的分析与计算操作呈现出各种各样的访存模式，使得上游的DGM系统难以预测即将到来的工作负载，无形中增加了DGM系统中存储空间分配与管理的代价。另一方面，图数据本身的不均匀特性容易导致DGM系统中各个线程的工作负载不均衡，但GPU的架构特性更适合运行负载均衡的任务。因此，faimgraph的一大设计原则在于最小化空间回收和重用的代价。

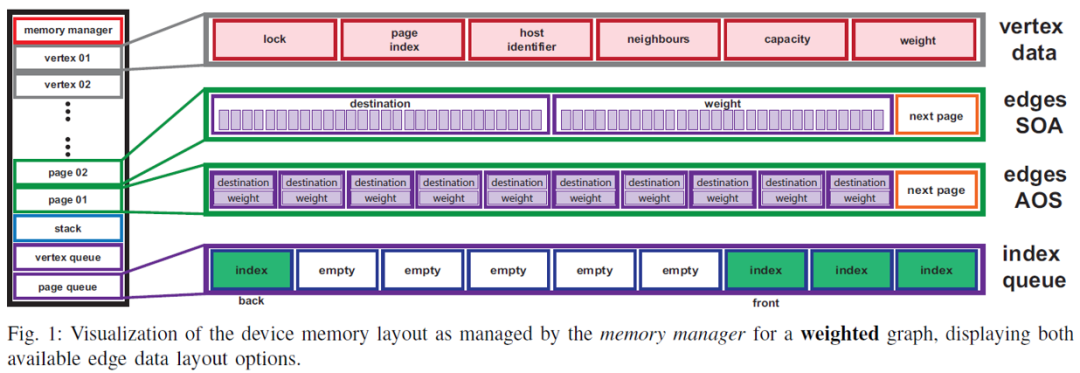
上图为faimgraph系统的框架。左侧不同颜色的方块代表了该系统的不同组成部分。总地说来，faimgraph由五个组件构成。一是全局的空间管理器，主要负责控制空间的分配和重用。二是点数据块，存储了每个点的属性与控制信息。三是页数据块，主要用于存储邻居列表。四是堆区，主要用于保存临时数据。五是空闲队列，分为点空闲队列和页空闲队列，用于记录可以回收的空间的标识符。

faimgraph在存储空间管理上的一个特点是所有的存储空间管理行为都在GPU端执行。由于CUDA框架中空间的申请操作需要由CPU端来发起，所以faimgraph中的一大核心思想是在系统初始化时向系统申请足够大的存储空间，随后的对这块存储空间的管理全部放在GPU端执行，从而减少大量的额外开销。一个全局的存储控制器管理着所有划分后的存储空间的元数据，以及图数据本身的一些属性。在执行增删改操作时产生的临时数据同样放在这块预先申请好的存储空间中，以堆的形式进行管理。

上述存储管理机制中的一个重要组成部分是空闲队列。空闲队列的主要作用为存储已经被释放的点数据存储空间和边数据存储页块的索引。在这些空间被交回给系统时，它们不会被真正释放，而是被记录在空闲队列中。对空间进行分配时，首先会检查空闲队列中是否有可重用的空间，若没有，才会在整个存储空间的对应区域中划分出新的存储块供使用。空闲队列的具体实现较为简单直接，其本质是一个基于数组的循环队列，通过维护两个声明为原子变量的指针（头指针和尾指针）和CAS操作来处理并发控制。

实际的图数据分别存储在点存储块和页存储块中。所有的点存储块的结构和大小相同，根据其在GPU端的标识符连续存储，构成一个动态增长的列表。新的点插入时，要么重用已被删除的结点，要么在列表的最后进行追加，不会触发在列表中间的删除和内容的移动。因此，通过使用原子的fetch-and-add操作为新插入的点赋予唯一的标识符即可实现上述操作。下图为点插入的伪代码。对即将执行插入操作的一批点，faimgraph系统首先将其根据标识符进行排序，排序的目的主要是进行一个批次内部的去重操作。同时，还需要对图数据中原有的点与即将插入的点进行比较。在这里作者提出了名为反向检查的优化。对图数据中原有的点与即将插入的点进行去重时，一般的逻辑为将即将插入的点作为搜索目标，在已有的点中进行搜索。而作者认为已有的点的数目远远多于即将插入的点的数目，这时单次搜索操作的耗时过长且负载不均衡。作者的解决方案是反其道而行之，将已有的点作为搜索目标，在即将插入的点中搜索。由于不同的点的搜索可以并行，作者此时实际上是通过提高并行度来弥补搜索次数的增加。

边数据的更新同样遵循类似的逻辑。如下图所示，首先对同一批次中的边进行排序，排序后检是否有重复的边，将重复的边去除后，开始实际的插入过程。每个线程处理一个点的邻居列表的插入。插入时的逻辑类似于归并排序，通过维护两个指针分别指向待插入的边表和原有的邻居列表，比较指针指向的元素的大小，根据大小关系移动元素或者指针。

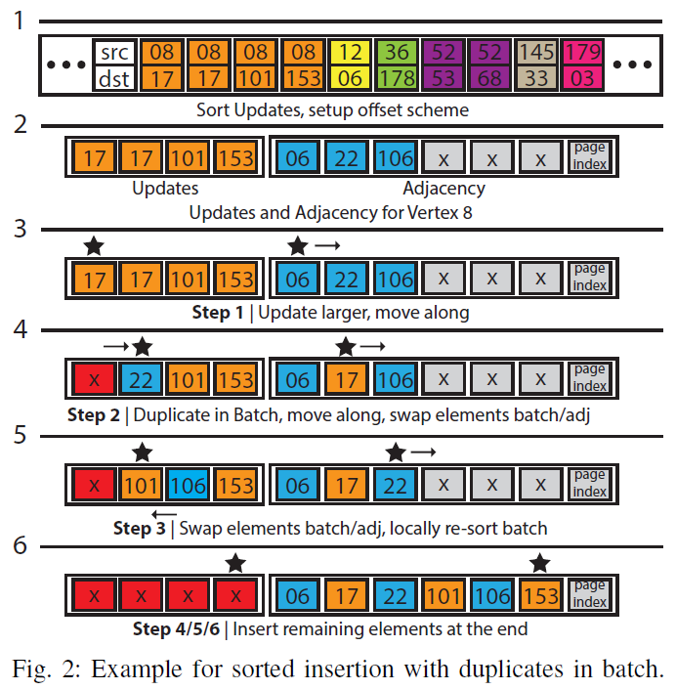
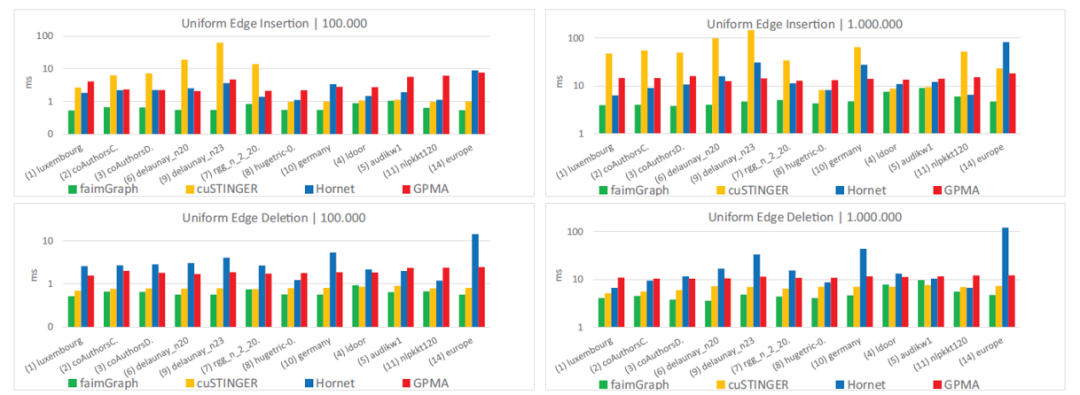
接下来介绍faimgraph的实验部分。首先是对不同批次下纯插入/删除的批次的性能比较。作者选取了cuSTINGER、Hornet与GPMA三个此前的系统进行比较。批次大小选择了100和1000两种。在绝大部分的数据集中faimgraph均取得了优势，性能提升2倍至10倍不等。并且在更新批次更大时，其性能优势更加显著。另外注意到cuSTINGER系统在不同数据集上的性能差距非常大，这主要取决于其是否触发了数据结构的重组操作。与之相比，faimgraph的表现在不同数据集上较为稳定。

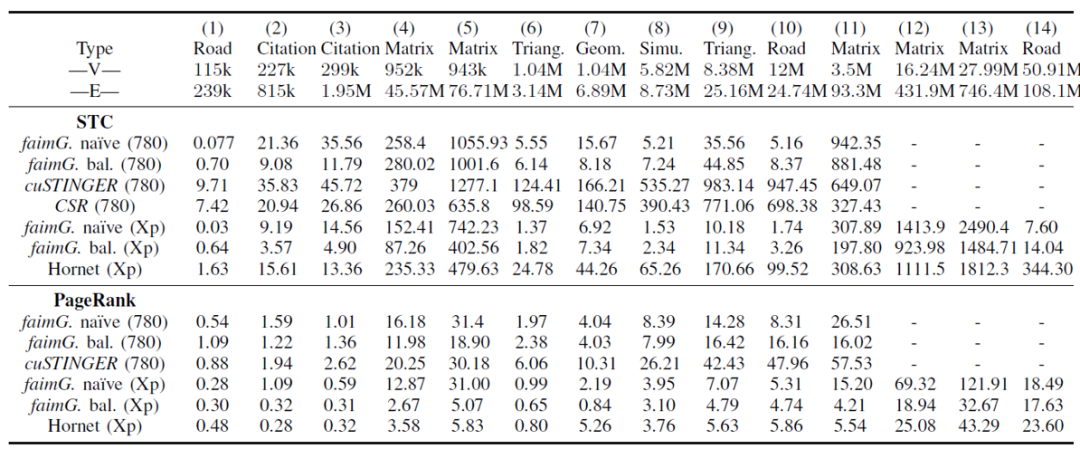
faimgraph的作者还比较了在不同的DGM系统上运行两种算法：三角形计数（Static Triangle Counting）和PageRank算法时的执行性能。可以看到在所有的数据集上faimgraph的性能都超过了先前的工作。并且在三角形计数这一算法上优势更加明显。

（二）Accelerating Dynamic Graph Analytics on GPUs

第二篇工作为来自新加坡国立大学的研究人员发表于SIGMOD2017的《Accelerating Dynamic Graph Analytics on GPUs》。其主要贡献为将一种自平衡的数据结构Packed Memoery Array（PMA）引入了GPU上的DGM系统中，为其设计了并发的更新机制，并探讨了如何将其与图算法进行结合。

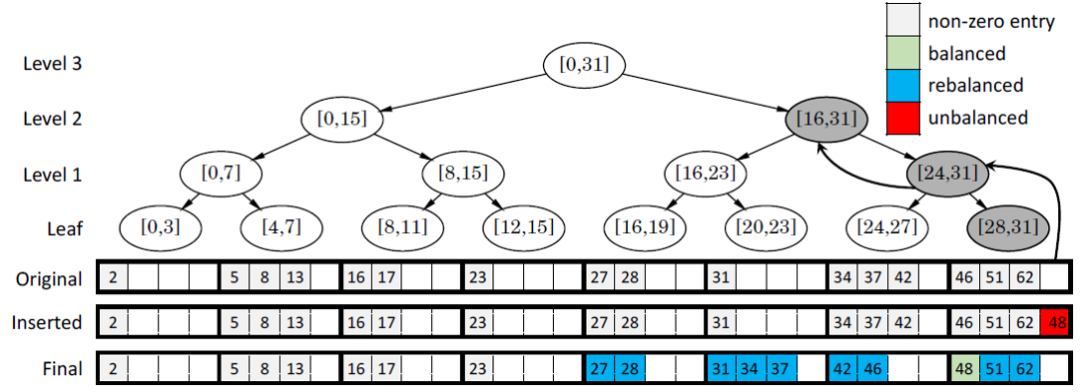
首先我们简单介绍PMA的原理。PMA是一种用于维护动态数组的数据结构。经典的顺序存储的数组在执行插入时需要移动插入位置之后的元素，产生大量额外开销。一种解决方案是在数组中预留出容纳插入元素的空位，PMA便是遵循这种思路，并且用一个平衡二叉树结构来维护这些空位。PMA首先将数组划分为等长的块，每个块中容纳元素的比例必须处于两个阈值之间，当这个比例不属于两个阈值之间时时，会沿平衡二叉树中的路径寻找连续的存储块，然后重新组织这些存储块中的元素，使得每个存储块中的容纳元素比例都符合阈值。如下图所示，在往数组中插入48以后，最后一个存储块的存储比例超过了阈值，这时，需要在平衡二叉树中往上搜索一层，找到最后两个存储块，发现仍然无法使得每个块都符合要求，因此还要再往上搜索一层，找到最后四个存储块，可以通过重新分配元素使得每个存储块中的存储元素比例都符合要求。

本文提出的GPMA方法的核心是在GPU上并发地对PMA进行插入的策略。如下图所示，每个线程负责一个元素的插入。当插入的元素位于不同的块并且不触发调整时，这些插入可以相互独立地并发执行。当插入元素导致阈值限制被破坏，则多个线程需要争抢锁来得到扩展的权力，而没有得到锁的线程需要等待到下一个迭代步才能够继续尝试完成自己的任务。

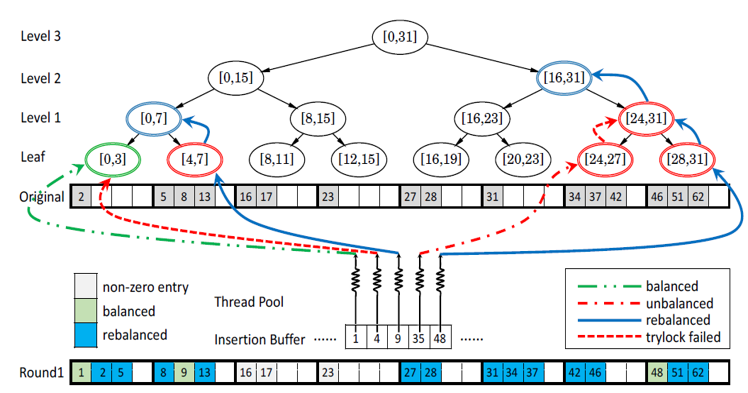
上述GPMA方案的问题有：第一，多个线程在访问时读取的数据不连续，无法利用GPU中访存合并的优化。第二，争抢锁的开销过大。第三，锁的争抢与随机的内存读取使得线程之间的工作负载不均衡且难以预测。为了解决上述三个问题，此文作者又提出了GPMA+方法。

GPMA+的算法思路如图所示，它与原来方案的不同在于，它首先对要插入的元素进行排序，排序可以在GPU上非常快速地执行。这时，要写到同一个存储块的插入元素被合并为一组，分别执行插入操作。在每一层都唤起所有的计算资源来处理一个组的插入操作。

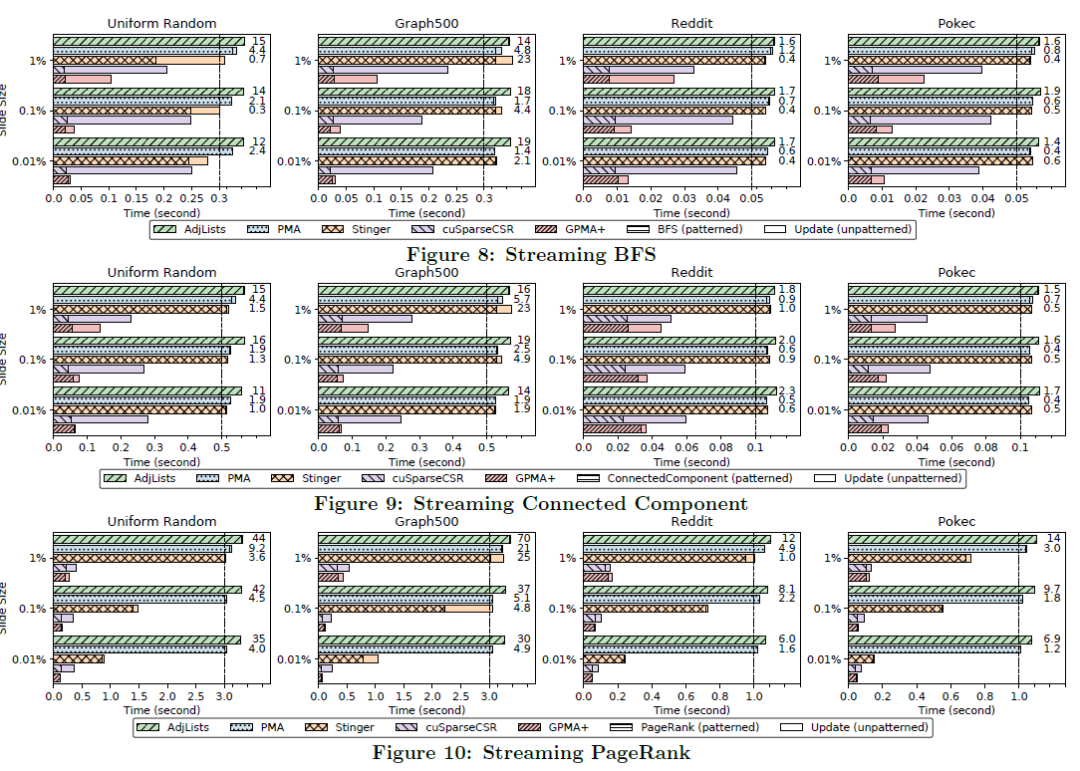
在实验中，GPMA和GPMA+方法在边更新操作、BFS、Connected component以及Pagerank算法中都取得了提升。

参考文献

[1] Winter, M. , et al. "faimGraph: High Performance Management of Fully-Dynamic Graphs Under Tight Memory Constraints on the GPU." SC18: International Conference for High Performance Computing, Networking, Storage and Analysis IEEE, 2019.

[2] Sha, M. , et al. "Accelerating dynamic graph analytics on GPUs." Proceedings of the VLDB Endowment 11.1(2017):107-120.