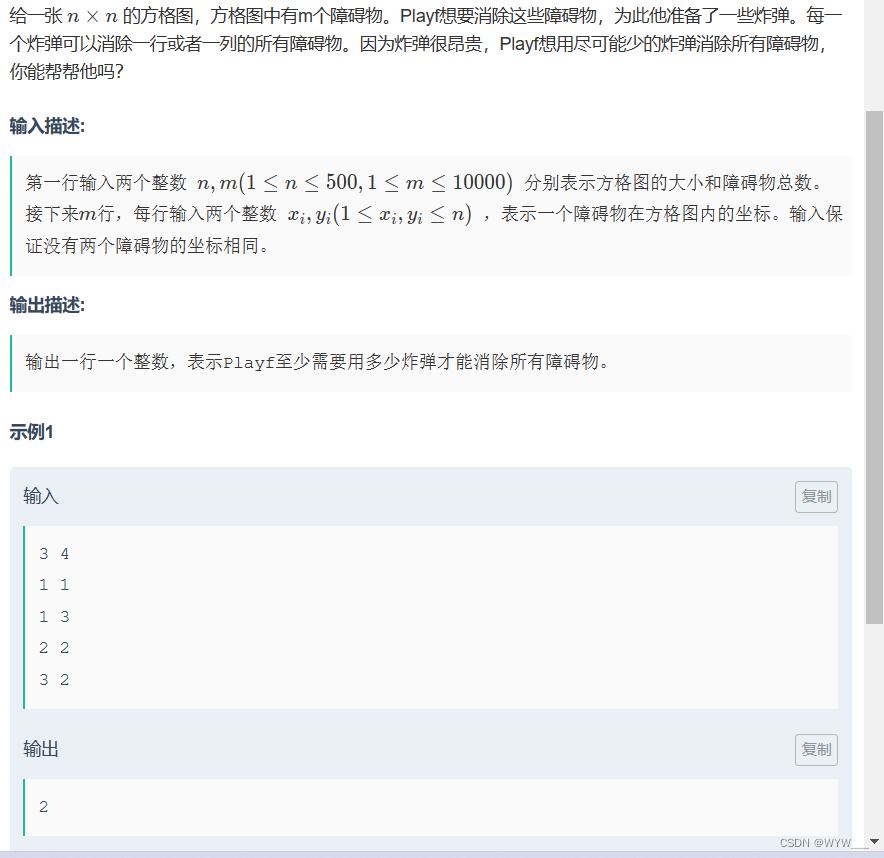
D-炸弹_2022图论班第一章图匹配例题与习题 (nowcoder.com)

看题解前先理解二分图最小点集覆盖 == 最大匹配

一、什么是最小点覆盖
点覆盖的概念定义：
对于图G=(V,E)中的一个点覆盖是一个集合S⊆V使得每一条边至少有一个端点在S中。
最小点覆盖：点个数最少的S集合。

这是我个人理解：↓（其实都一样）
最小点覆盖，就是二分图中每个边至少一个端点在该点集中 的 最小点集。

二、证明
最小点集覆盖 == 最大匹配

①最小点集覆盖<=最大匹配，
假设最小点集覆盖为n, 那么一定能构造出一个为n的匹配， 显然这个匹配<= 最大匹配

②最小点集覆盖 >= 最大匹配。

假设最大匹配为n，所以肯定有n条边，他们的端点互不相同。 因此我们要覆盖这n条边至少要n个定点。

所以 最小点集覆盖>= 最大匹配。

综上：

最小点集覆盖 == 最大匹配

所以可以通过二分图匹配，匈牙利算法来解决最小点覆盖问题

题解:

我们可以把行于列转化为二分图的左部与右部,每一颗陨石都转化为一条边,题目就变成了最小点覆盖问题,二最小点覆盖有等于最大匹配,所以我们直接求我们建的图的最大匹配即可

#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
#include<set>
using namespace std;
#define int long long
int n,m;
int vis[505];
int a[505][505];
int link[505];
int dfs(int x)
{
	for(int i = 1;i <= n;i++)
	{
		if(!vis[i]&&a[x][i])
		{
			vis[i] = 1;
			if(!link[i]||dfs(link[i]))
			{
				link[i] = x;
				return 1;
			}
		}
	}
	return 0;
}
void solve()
{
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		int x,y;
		cin >> x >> y;
		a[x][y] = 1; 
	}
	int res = 0;
	for(int i = 1;i <= n;i++)
	{
		memset(vis,0,sizeof vis);
		if(dfs(i))
		res++;
	}
	cout <<res;
}
//17 5
//
signed main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int t = 1;
//	cin >> t;
    while(t--)
	{

		solve();
	} 
}