目录
三数之和
电话号码的字母组合
括号生成
合并k个升序链表
下一个排列
搜索旋转排序数组
在排序数组中查找元素的第一个和最后一个位置
组合总数
全排列
旋转图像
三数之和
题目链接:15.三数之和
 示例
示例
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
解题思路
双指针思想,先对数组进行排序,排序后从第一个位置开始枚举,需要确保下一个枚举的数不等于本次枚举的数,如果相等,得到的结果是相同的。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
int n = nums.length;
Arrays.sort(nums);
List<List<Integer>> ret = new ArrayList<>();
for (int first = 0; first < n; first++) {
//保证与上一次枚举的数不同
if (first > 0 && nums[first] == nums[first - 1]) {
continue;
}
int third = n - 1;
int target = -nums[first];
//-4 -1 -1 0 1 2
for (int second = first + 1; second < nums.length; second++) {
//保证与上一次枚举的不同
if (second > first + 1 && nums[second] == nums[second - 1]) {
continue;
}
//保证second在third的左边
while (second < third && nums[second] + nums[third] > target) {
third--;
}
//指针重合就退出循环
if (second == third) {
break;
}
if (nums[second] + nums[third] == target) {
List<Integer> list = new ArrayList<>();
list.add(nums[first]);
list.add(nums[second]);
list.add(nums[third]);
ret.add(list);
}
}
}
return ret;
}
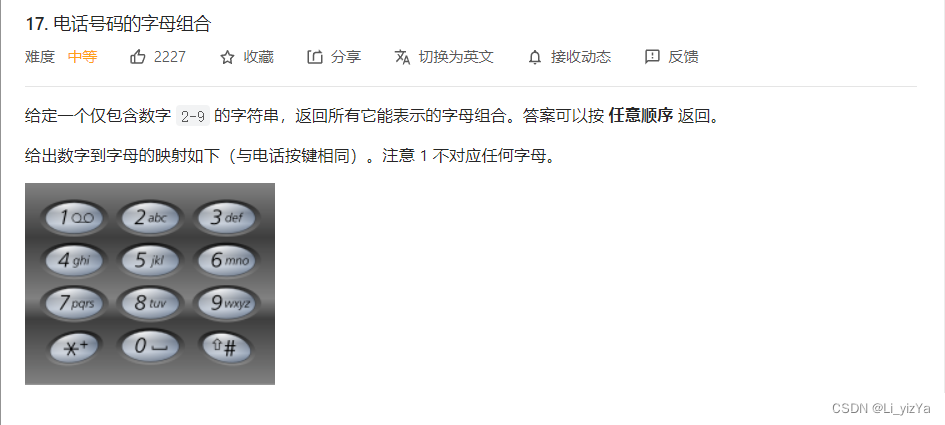
}电话号码的字母组合
题目链接:17.电话号码的字母组合
示例
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
解题思路
维护一个深度和当前的可能的字母组合,当输入的数字长度等于深度时,就将当前的字母组合加入到结果集中,结束该路径并继续向上回溯;根据深度找到当前的数字,再根据这个数字得到该数字所代表的字符,依次遍历每一种可能,直至所有字符遍历结束。
class Solution {
String[] mapString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
List<String> ret = new ArrayList<>();
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return ret;
}
StringBuilder s = new StringBuilder("");
dfs(digits, s, 0);
return ret;
}
private void dfs(String digits, StringBuilder s, int depth) {
if (depth == digits.length()) {
ret.add(s.toString());
return;
}
int index = digits.charAt(depth) - '0';
String curMap = mapString[index];
for (int i = 0; i < curMap.length(); i++) {
dfs(digits, s.append(curMap.charAt(i)), depth + 1);
s.deleteCharAt(s.length() - 1);
}
}
}括号生成
题目链接: 22.括号生成
解题思路
回溯思想,只在序列有效时添加括号,通过跟踪当前的左括号和右括号数来实现,如果左括号数量不大于n,添加左括号,如果右括号数量小于左括号,添加左括号,当括号数量等于2*n,加入结果集
class Solution {
public List<String> generateParenthesis(int n) {
List<String> ret = new ArrayList<>();
dfs(ret, new StringBuilder(), 0, 0, n);
return ret;
}
private void dfs(List<String> ret, StringBuilder cur, int open, int close, int n) {
if (cur.length() == n * 2) {
ret.add(cur.toString());
return;
}
if (n > open) {
cur.append('(');
dfs(ret, cur, open + 1, close, n);
cur.deleteCharAt(cur.length() - 1);
}
if (open > close) {
cur.append(')');
dfs(ret, cur, open, close + 1, n);
cur.deleteCharAt(cur.length() - 1);
}
}
}合并k个升序链表
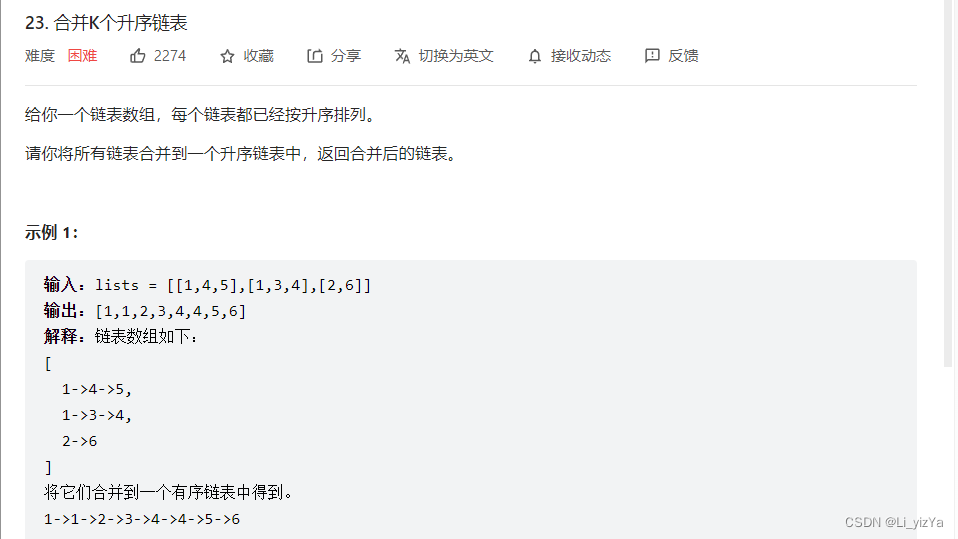
题目链接:23.合并k个升序链表
解题思路
分治思想,要合并k个升序链表,则首先将每两个链表合并,第一轮合并过后,继续两两合并,直至得到最终结果。
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0) {
return null;
}
return merge(lists, 0, lists.length - 1);
}
private ListNode merge(ListNode[] lists, int start, int end) {
if (start == end) {
return lists[end];
}
int mid = (start + end) / 2;
ListNode l1 = merge(lists, start, mid);
ListNode l2 = merge(lists, mid + 1, end);
return mergeTwoList(l1, l2);
}
private ListNode mergeTwoList(ListNode l1, ListNode l2) {
if (l1 == null || l2 == null) {
return l1 == null ? l2 : l1;
}
if (l1.val > l2.val) {
l2.next = mergeTwoList(l1, l2.next);
return l2;
} else {
l1.next = mergeTwoList(l1.next, l2);
return l1;
}
}
}下一个排列
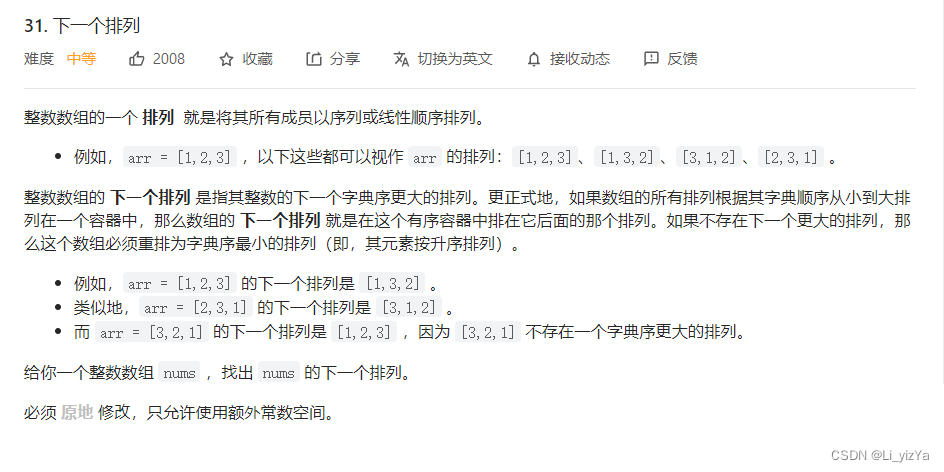
题目链接:31.下一个排列
 示例
示例
输入:nums = [1,2,3]
输出:[1,3,2]
解题思路:将左边的一个较小数与右边的一个较大数进行交换,需要满足左边的较小数尽可能靠右,较大数尽可能的小,再交换结束后,再将较大数右边的数按照升序重新排列即可
class Solution {
public void nextPermutation(int[] nums) {
//8 5 3 6 2 1
int i = nums.length - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = nums.length - 1;
while (j >= 0 && nums[j] <= nums[i]) {
j--;
}
swap(nums, i, j);
}
reverse(nums, i + 1);
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
private void reverse(int[] nums, int start) {
int end = nums.length - 1;
while (start < end) {
swap(nums, start, end);
start++;
end--;
}
}
}搜索旋转排序数组
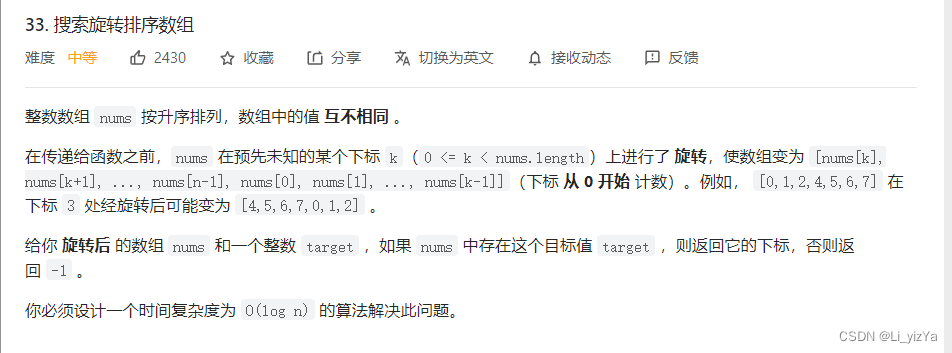
题目链接:33. 搜索旋转排序数组
示例
输入:nums = [
4,5,6,7,0,1,2], target = 0输出:4
解题思路:二分思想,查找相当于是不断地缩小范围,通过nums[mid]、nums[left]、nums[right]、target的对比,不断缩小范围,直至获得结果或者左边界left > 右边界right为止.
class Solution {
//1 2 3 4 5
//2 3 4 5 1
//5 1 2 3 4
public int search(int[] nums, int target) {
if (nums.length == 0 || nums == null) {
return -1;
}
if (nums.length == 1) {
return nums[0] == target ? 0 : -1;
}
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
return mid;
}
if (nums[left] <= nums[mid]) {
if (nums[mid] >= target && nums[left] <= target) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if (nums[right] >= target && nums[mid] <= target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
}在排序数组中查找元素的第一个和最后一个位置
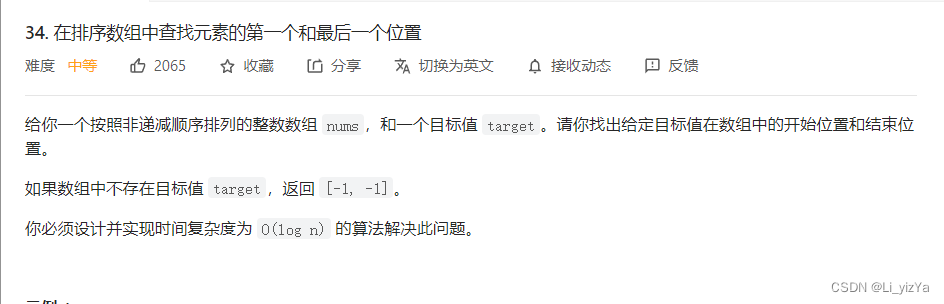
题目链接:34. 在排序数组中查找元素的第一个和最后一个位置
示例
输入:nums = [
5,7,7,8,8,10], target = 8输出:[3,4]
输入:nums = [
5,7,7,8,8,10], target = 6输出:[-1,-1]
解题思路:二分查找,查找第一个大于等于target的下标位置,即为第一个位置,查找第一个大于target的下标,即为最后一个位置,因为可能不存在target,因此在查询结束后验证一下left和right下标对应的值是否为target,如果是则输出,left,right,反之输出-1,-1.
class Solution {
public int[] searchRange(int[] nums, int target) {
int left = binarySearch(nums, target, true);
int right = binarySearch(nums, target, false) - 1;
if (left <= right && right < nums.length && nums[left] == target && nums[right] == target) {
return new int[]{left, right};
}
return new int[]{-1, -1};
}
private int binarySearch(int[] nums, int target, boolean lower) {
int left = 0;
int right = nums.length - 1;
int ret = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ret = mid;
} else {
left = mid + 1;
}
}
return ret;
}
}组合总数
题目链接:39. 组合总和
 示例
示例
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
解题思路:由于同一个数字可以无限制重复被选取,因此每次从上一个位置开始搜索,边界值的设定:当目前的累加值大于给定的值就返回,当累加值等于给定的值就将其加入结果集中。
class Solution {
List<List<Integer>> ret = new ArrayList<>();
List<Integer> curRet = new ArrayList<>();
int curAdd = 0;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
if (candidates == null || candidates.length == 0) {
return ret;
}
dfs(candidates, target, 0);
return ret;
}
private void dfs(int[] candidates, int target, int pre) {
if (curAdd > target) {
return;
}
if (curAdd == target) {
ret.add(new ArrayList<>(curRet));
return;
}
for(int i = pre; i < candidates.length; i++) {
if (candidates[i] > target) {
continue;
}
curRet.add(candidates[i]);
curAdd += candidates[i];
dfs(candidates, target, i);
curAdd -= curRet.get(curRet.size() - 1);
curRet.remove(curRet.size() - 1);
}
}
}全排列
题目链接:46. 全排列

示例
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
解题思路:回溯算法,依次从每个位置开始添加元素,注意需要维护一个数组来记录每个下标对应的值是否已经添加到排列中,如果已经添加则不需要继续添加,反之,则添加入排列中。
class Solution {
List<List<Integer>> ret = new ArrayList<>();
List<Integer> curRet = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
if (nums == null || nums.length == 0) {
return ret;
}
int[] visited = new int[nums.length];
dfs(nums, visited);
return ret;
}
private void dfs(int[] nums, int[] visited) {
if (curRet.size() == nums.length) {
ret.add(new ArrayList<>(curRet));
return;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i] == 1) {
continue;
}
visited[i] = 1;
curRet.add(nums[i]);
dfs(nums, visited);
visited[i] = 0;
curRet.remove(curRet.size() - 1);
}
}
}旋转图像
题目链接:48. 旋转图像

解题思路:找规律问题,先水平翻转一次,再沿着对角线翻转一次即可得到结果
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//水平翻转
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = tmp;
}
}
//对角线翻转
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
}
}