一起学数据结构（9）——二叉树的链式存储及相关功能实现

news2024/11/20 20:24:59

     

目录

1. 二叉树的链式存储：

2. 二叉树的前序遍历：

3. 二叉树的中序遍历：

4. 二叉树的后序遍历：

5. 统计二叉树的结点总数

 

6.统计二叉树的叶子结点数：

7. 统计二叉树第层的结点数量：

8. 二叉树的销毁：

9.查找树中值为结点：

10. 二叉树的层序遍历：

11. 代码总览：

11.1 头文件TRLIst.h

11.2 函数实现文件TRList.c

11.3 函数测试文件Test.c

  在数据结构的第七篇文章中提到，对于完全二叉树而言，可以采用顺序存储的方法来存储完全二叉树。但是对于非完全二叉树而言，（例如下图中给出的二叉树）存储方法需要采用链式存储。本文将围绕二叉树的链式存储展开，介绍链式存储方法以及此类二叉树相关功能的实现。

1. 二叉树的链式存储：

        在前几篇文章介绍完全二叉树及堆的代码实现时，会涉及到此类数据结构的插入结点、删除结点等特点。但是，对于非完全二叉树，由于结构并不像完全二叉树一样有一定规律，因此，利用非完全二叉树存储数据的操作较为复杂。并且，在存储数据这一方面，之前的完全二叉树更为合适。所以，对于普通的非完全二叉树来说，插入、删除结点的操作是没有意义的。

       对于非完全二叉树的价值，主要是体现于后续更复杂的数据结构中，例如红黑树等。因此，文章后续实现的功能主要是利用递归来针对于非完全二叉树自身而言，例如求非完全二叉树的叶子结点数目，二叉树的深度等等。在二叉树的链式存储这一部分，将通过构建关于新建结点函数BuyTRNode来手动构建上图给出的非完全二叉树。

       对于非完全二叉树，在关于树的基础的文章中就提到，链式存储的方法可以归结为左孩子，右兄弟。所以，树的结点的结构如下：

typedef int TRDataType;
typedef struct TreeNode
{
	TRDataType val;
	struct TreeNode* left;
	struct TreeNode* right;
}TRNode;

   在确立了二叉树结点的结构之后，下一步构建函数BuyTRNode，代码如下：

TRNode* BuyTRNode(int x)
{
	TRNode* newnode = (TRNode*)malloc(sizeof(TRNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->val = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

下一步，通过上面的两个函数，直接构建出上图中给出的非完全二叉树，即：

int main()
{
	TRNode* node1 = BuyTRNode(1);
	TRNode* node2 = BuyTRNode(2);
	TRNode* node3 = BuyTRNode(3);
	TRNode* node4 = BuyTRNode(4);
	TRNode* node5 = BuyTRNode(5);
	TRNode* node6 = BuyTRNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return 0;
}

（注： 文章后续所有的运行结果均需要适配相应的测试代码，测试代码将在文章最后统一给出）

2. 二叉树的前序遍历：

对于二叉树的前序遍历，其顺序是按照：根结点，左结点，右结点进行访问的，例如对于上面给出的树：其结点访问顺序依次为（注：将空看作NULL结点）：1，2，3，NULL,NULL,NULL,4,5,NULL,NULL,6,NULL,NULL。

利用图形来表示结点访问的顺序，即：

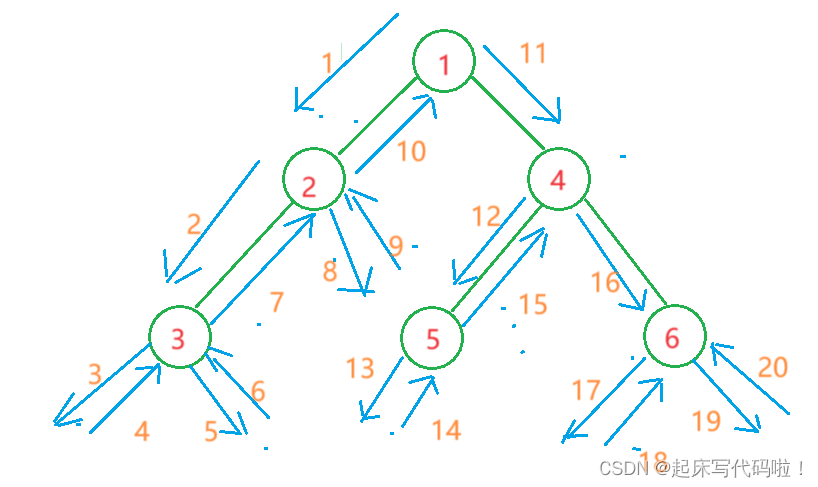
其中3,5,8,13,17,19均代表访问到空结点，4,6,9,14,20代表访问到空结点后，返回上一个结点。在结点访问的过程中，每个结点都是按照：根结点、左结点、右结点的顺序。因此，对于这种重复性的问题，可以使用递归实现，具体代码如下：

//前序遍历
void PreOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问根结点：
	printf("%d ", root->val);
	//访问左结点：
	PreOrder(root->left);
	//访问右结点：
	PreOrder(root->right);
}

运行结果如下：

3. 二叉树的中序遍历：

       二叉树的中序遍历顺序为：左结点、根结点、右结点，依旧针对于上面给出的二叉树，中序遍历对于结点的访问顺序为：NULL，3，NULL，2，NULL，1，NULL，5，NULL，4，NULL，6NULL。用图片表示结点的访问顺序，即：

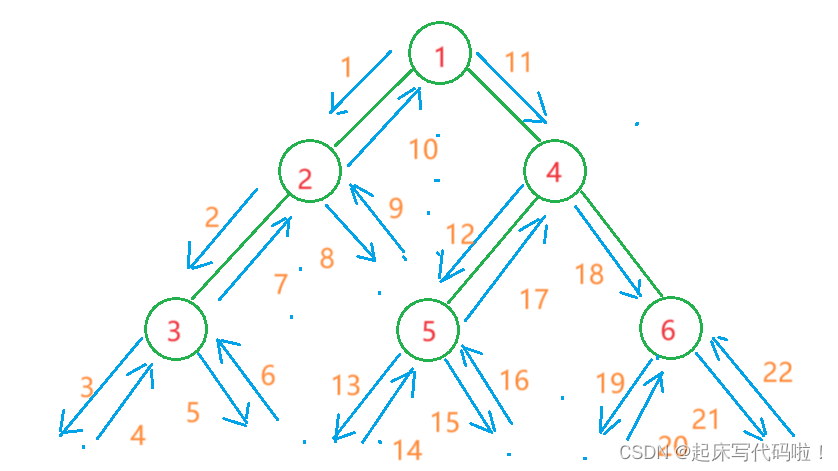
对应代码如下：

//中序遍历
void InOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问左结点：
	InOrder(root->left);
	//访问根结点：
	printf("%d ", root->val);
	//访问右结点：
	InOrder(root->right);
}

结果如下：

4. 二叉树的后序遍历：

二叉树的后序遍历顺序为：左结点，右结点，根结点。针对上方给出的二叉树，后序遍历访问结点的顺序依次为：NULL，NULL，3，NULL，2，NULL，NULL，5，NULL，NULL，6，4，1。

用图形表示结点的访问顺序，即：

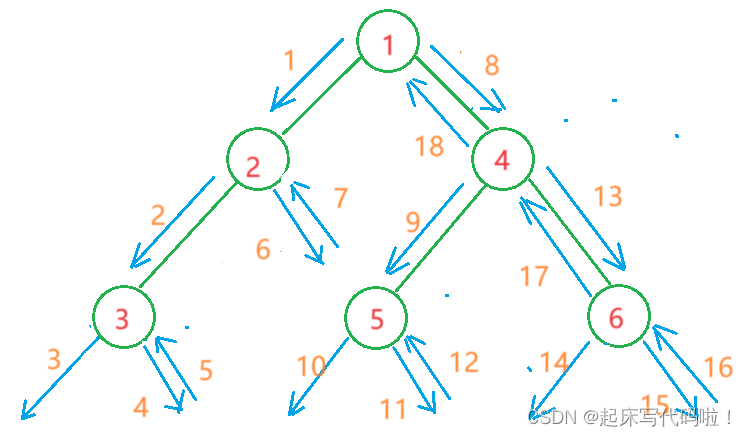
对应代码如下：

//后序遍历
void PostOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问左结点：
	InOrder(root->left);
	//访问右结点：
	InOrder(root->right);
	//访问根结点：
	printf("%d ", root->val);

}

结果如下： 

5. 统计二叉树的结点总数

对于统计二叉树的结点总数这一功能，可以拆分为以下步骤利用递归进行实现：

1. 检测结点是否为空，如果为空，则表示结点为空，即不存在此结点，返回0。如果不为空，则表示存在本结点，结果加1并且向下检测本结点的左、右结点。

2.在检测结点时，需要检测结点的左、右结点，检测方法参考1

具体代码如下：

//统计二叉树的结点树：
int TreeSize(TRNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

测试结果如下：

 

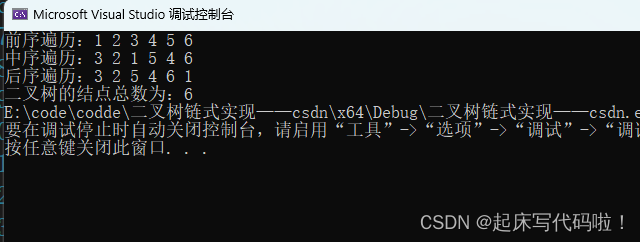
6.统计二叉树的叶子结点数：

对于统计二叉树叶子结点数的功能实现，可以分成下面的部分：

1. 检测本结点是否符合叶子结点的特点，即：root->left= NULL,并且root->right = NULL。如果符合，则返回值返回1。

2.若本结点不符合1中的判定条件，则存在两种情况，一是本结点为空，二是本结点为分支结点。对于第一种情况，返回值返回0，对于第二种情况，则继续向下检测本结点的子结点，即root->left,root->right

对应代码为：

//统计二叉树的叶子结点数：
int TreeLeafSize(TRNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

运行结果如下：

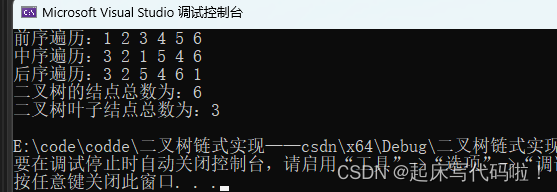
符合上图中的叶子结点数量。

7. 统计二叉树第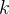k层的结点数量：

对于此功能的实现，同样可以分为下面的几步：

1.额外创建一个变量k，用k来间接表示二叉树的层数，每经过依次递归，对k进行一次-1的操作。当k=0时，表示已经到达目标层数。此时，如果目标层存在结点，则返回值返回1.

2.当k\neq 0时，表示还未到达目标层数，继续向下遍历该结点左、右两个子结点。

3.在函数传参的时候，需要注意，不能传递k，需要传递k-1。具体代码如下：

//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 0)
	{
		return 1;
	}

	return TNodeSize(root->left, k - 1) + TNodeSize(root->right, k - 1);
}

运行结果如下：


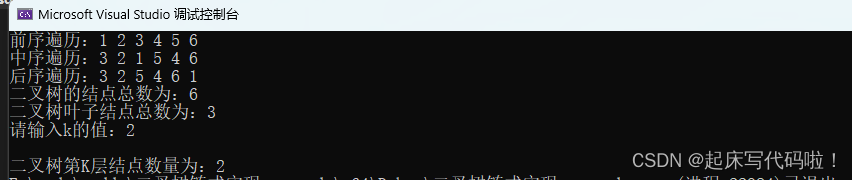
结点数量符合上方给出的二叉树。 

8. 二叉树的销毁：

原理较为简单，只给出代码，不做过多解释：

//二叉树的销毁
void TNodeDestory(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}
	TNodeDestory(root->left);
	TNodeDestory(root->right);

	free(root);
}

9.查找树中值为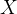X结点：

对于查找树中值为X的结点这一功能，可以分成下面的步骤实现：

1. 检测本结点是否为空，如果为空则返回NULL。

2.若本结点不为空，则检测本结点中存储的数值是否=X，若符合条件，则返回该结点的地址。

3.此时，结点即不为空，结点中存储的数值也\neq X，因此，继续遍历该结点的左、右两个子结点。

对于函数返回值的处理，可以在函数中额外创建一个函数指针，为了方便表达，将这个指针命名为ret。

如果函数的根结点中存储的数值就是X，则直接返回该结点指针。如果不等于，按照上面的思路，函数会继续遍历根结点的子结点。直接令ret接收函数的返回值，并且，在遍历的后方加上对于ret的判定。由于ret的返回值只存在两种情况，即NULL,root。所以，如果ret返回值不为ret，则不允许返回返回值。判定ret的返回值为root，则返回返回值。如果在函数遍历的过程中，所有的ret都不允许返回，则表示树种不存在存储数值为X的结点。直接返回NULL

对应代码如下：

//查找树中值为x的结点：
TRNode* TRFind(TRNode* root,int x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val = x)
	{
		return root;
	}

	TRNode* ret = NULL;
	ret = TRFind(root->left, x);
	if (ret)
	{
			return ret;
	}
	ret = TRFind(root->right, x);
	if (ret)
	{
		return ret;
	}

	return NULL;
}

运行结果如下：

10. 二叉树的层序遍历：

对于二叉树的层序遍历，由于需要每一层挨个访问结点，因此，不能再用前面递归的思想来实现此功能 。如果不采用递归，则必须对每个结点的数值进行一次存储。所以，文章这里利用队列来辅助实现二叉树的层序遍历

（注：关于队列的相关知识及代码，可在前面的文章一起学数据结构（6）——栈和队列-CSDN博客获取，需要注意，在实现本功能时，需要将队列头文件中，typedef  int  QDataType改成typedef TreeNode  QDataType以便匹配后序的返回值）

实现本功能的具体思路如下：

1. 创建一个队列，为了方便表达，将这个队列命名为qs。

2. 先往队列中利用插入函数QNodePush插入二叉树根结点的数值。

3. 创建一个指针，命名为violent，利用这个指针来接受QueuePop函数(取队头元素函数)的返回值（返回值返回该结点的地址)。

4.按照层序遍历的顺序(即：一层一层，从左到右访问结点)，向队列中插入数据，顺序为：插入左子结点，插入右子结点

5.销毁队头指针，利用循环配合上述步骤来完成对整个二叉树的访问，判定条件为!QueueEmpty(探空函数）

对应代码如下：
 

//层序遍历
void LevelOrder(Que* qs,TRNode* root)
{
	if(root)
	QueuePush(qs, root);

	while (!QueueEmpty(qs))
	{
		TRNode* violent = QueueFront(qs);
		printf("%d ", violent->val);

		if (violent->left)
			QueuePush(qs,violent->left);
		if (violent->right)
			QueuePush(qs,violent->right);

		QueuePop(qs);
	}


}

运行结果如下：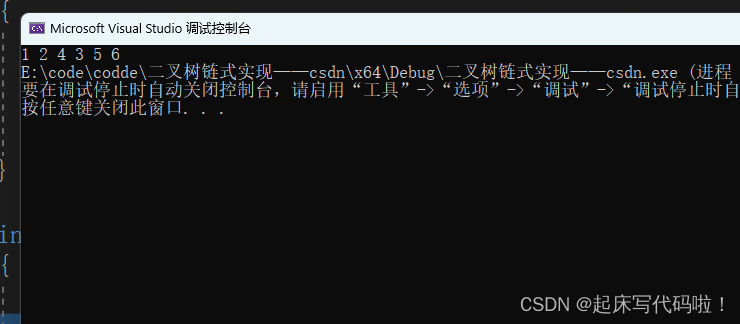

 

11. 代码总览：

11.1 头文件TRLIst.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int TRDataType;
typedef struct TreeNode
{
	TRDataType val;
	struct TreeNode* left;
	struct TreeNode* right;
}TRNode;

#include"queue.h"

//结点插入函数
TRNode* BuyTRNode(int x);

//前序遍历
void PreOrder(TRNode* root);

//中序遍历
void InOrder(TRNode* root);

//后序遍历
void PostOrder(TRNode* root);

//统计二叉树的结点树：
int TreeSize(TRNode* root);

//统计二叉树的叶子结点数：
int TreeLeafSize(TRNode* root);

//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k);

//二叉树的销毁
void TNodeDestory(TRNode* root);

//查找树中值为x的结点：
TRNode* TRFind(TRNode* root, int x);

//层序遍历
void LevelOrder(Que* qs,TRNode* root);

11.2 函数实现文件TRList.c

#include"TRList.h"

//结点插入函数
TRNode* BuyTRNode(int x)
{
	TRNode* newnode = (TRNode*)malloc(sizeof(TRNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->val = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

//前序遍历
void PreOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问根结点：
	printf("%d ", root->val);
	//访问左结点：
	PreOrder(root->left);
	//访问右结点：
	PreOrder(root->right);
}

//中序遍历
void InOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问左结点：
	InOrder(root->left);
	//访问根结点：
	printf("%d ", root->val);
	//访问右结点：
	InOrder(root->right);
}

//后序遍历
void PostOrder(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//访问左结点：
	InOrder(root->left);
	//访问右结点：
	InOrder(root->right);
	//访问根结点：
	printf("%d ", root->val);
}

//统计二叉树的结点树：
int TreeSize(TRNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

//统计二叉树的叶子结点数：
int TreeLeafSize(TRNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

//统计二叉树第k层结点数
int TNodeSize(TRNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 0)
	{
		return 1;
	}

	return TNodeSize(root->left, k - 1) + TNodeSize(root->right, k - 1);
}

//二叉树的销毁
void TNodeDestory(TRNode* root)
{
	if (root == NULL)
	{
		return;
	}
	TNodeDestory(root->left);
	TNodeDestory(root->right);

	free(root);
}

//查找树中值为x的结点：
TRNode* TRFind(TRNode* root,int x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val = x)
	{
		return root;
	}

	TRNode* ret = NULL;
	ret = TRFind(root->left, x);
	if (ret)
	{
			return ret;
	}
	ret = TRFind(root->right, x);
	if (ret)
	{
		return ret;
	}

	return NULL;
}

//层序遍历
void LevelOrder(Que* qs,TRNode* root)
{
	if(root)
	QueuePush(qs, root);

	while (!QueueEmpty(qs))
	{
		TRNode* violent = QueueFront(qs);
		printf("%d ", violent->val);

		if (violent->left)
			QueuePush(qs,violent->left);
		if (violent->right)
			QueuePush(qs,violent->right);

		QueuePop(qs);
	}


}

11.3 函数测试文件Test.c

#include"TRList.h"


void TestOrder(TRNode* root)
{
	printf("前序遍历：");
	PreOrder(root);
	printf("\n");
	printf("中序遍历：");
	InOrder(root);
	printf("\n");
	printf("后序遍历：");
	PostOrder(root);
	printf("\n");
}

void TestNode(TRNode* root)
{
	printf("二叉树的结点总数为：");
	int sum = TreeSize(root);
	printf("%d ", sum);
	printf("\n");
	int sum1 = TreeLeafSize(root);
	printf("二叉树叶子结点总数为：");
	printf("%d ", sum1);
	printf("\n");
	
	int k = 0;
	printf("请输入k的值：");
	scanf("%d", &k);
	int sum2 = TNodeSize(root, k-1);
	printf("\n");
	printf("二叉树第K层结点数量为：");
	printf("%d ", sum2);
	printf("\n");
}

void TestTRDes(TRNode* root)
{
	printf("请输入想要查找的值：");
	int x = 0;
	scanf("%d", &x);
	TRNode* ret = NULL;
	ret = TRFind(root, x);
	printf("\n");
}



void TestLOrder(TRNode* root)
{
	Que qs;
	QueueInit(&qs);
	LevelOrder(&qs, root);
	QueueDestory(&qs);
}

int main()
{
	TRNode* node1 = BuyTRNode(1);
	TRNode* node2 = BuyTRNode(2);
	TRNode* node3 = BuyTRNode(3);
	TRNode* node4 = BuyTRNode(4);
	TRNode* node5 = BuyTRNode(5);
	TRNode* node6 = BuyTRNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;


	TestOrder(node1);
	TestNode(node1);
	TestTRDes(node1);
	TestLOrder(node1);
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1109063.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何修改模型颜色

如何修改模型颜色

1、模型材质颜色介绍 在3D模型中&#xff0c;材质&#xff08;Material&#xff09;是指表面质感的特性&#xff0c;包括颜色、光泽、透明度等属性。其中&#xff0c;颜色是最基本的属性之一&#xff0c;它决定了物体表面的外观和感觉。 在现代计算机图形学中&#xff0c;通常…
阅读更多...
使用 Typhoeus 和 Ruby 编写的爬虫程序

使用 Typhoeus 和 Ruby 编写的爬虫程序

以下是一个使用 Typhoeus 和 Ruby 编写的爬虫程序&#xff0c;用于爬取 &#xff0c;同时使用了 jshk.com.cn/get_proxy 这段代码获取代理&#xff1a; #!/usr/bin/env rubyrequire typhoeus require jsondef get_proxyurl "https://www.duoip.cn/get_proxy"respon…
阅读更多...
CTF是黑客大赛？新手如何入门CTF？

CTF是黑客大赛？新手如何入门CTF？

CTF是啥 CTF 是 Capture The Flag 的简称&#xff0c;中文咱们叫夺旗赛&#xff0c;其本意是西方的一种传统运动。在比赛上两军会互相争夺旗帜&#xff0c;当有一方的旗帜已被敌军夺取&#xff0c;就代表了那一方的战败。在信息安全领域的 CTF 是说&#xff0c;通过各种攻击手…
阅读更多...
随手记录第十话 -- 升级SpringBoot3.0 + JDK17的踩坑记录

随手记录第十话 -- 升级SpringBoot3.0 + JDK17的踩坑记录

随着有些jar包的升级&#xff0c;JDK1.8已经不是最稳定的版本了。 前段时间接触到Web3相关&#xff0c;jar包的编译最低要JDK13了&#xff0c;碰巧另一个使用Kotlin写的jar包依赖需要17了&#xff0c;那就直接上17吧&#xff0c;同时Springboot也上到3.0。 1. 框架说明 Spri…
阅读更多...
哪个牌子的护眼灯防蓝光效果好？2023防蓝光护眼灯推荐

哪个牌子的护眼灯防蓝光效果好？2023防蓝光护眼灯推荐

可以肯定的是&#xff0c;护眼灯一般可以达到护眼的效果。 看书和写字时&#xff0c;光线应适度&#xff0c;不宜过强或过暗&#xff0c;护眼灯光线较柔和&#xff0c;通常并不刺眼&#xff0c;眼球容易适应&#xff0c;可以防止光线过强或过暗导致的用眼疲劳。如果平时生活中需…
阅读更多...
Python国庆祝福

Python国庆祝福

系列文章 序号文章目录直达链接1浪漫520表白代码https://want595.blog.csdn.net/article/details/1306668812满屏表白代码https://want595.blog.csdn.net/article/details/1297945183跳动的爱心https://want595.blog.csdn.net/article/details/1295031234漂浮爱心https://want…
阅读更多...
软件开发线上维护方案

软件开发线上维护方案

编写软件维护方案是确保软件系统长期稳定运行和满足不断变化需求的关键步骤。以下是编写软件维护方案的一般步骤和建议&#xff0c;希望对大家有所帮助。北京木奇移动技术有限公司&#xff0c;专业的软件外包开发公司&#xff0c;欢迎交流合作。 文档概述&#xff1a; 开始文档…
阅读更多...
Java （day 3）方法、数组、面向对象和异常

Java （day 3）方法、数组、面向对象和异常

Java方法、数组、面向对象和异常 1.方法1.1 什么是方法&#xff1f;1.2 方法的定义1.3 方法的调用1.4 值传递和引用传递1.5 方法的重载1.6 命令行传参1.7 可变参数1.8 递归 2.数组2.1 数组概述2.2 数组声明创建2.3 三种初始化及内存分析和总结&#xff08;1&#xff09;java内存…
阅读更多...
前端本地开发中，代理配置是如何解决跨域的？

前端本地开发中，代理配置是如何解决跨域的？

文章目录 跨域&#xff08;Cross-Origin&#xff09;开发代理原理先说一下三个概念那代理到底是如何解决跨域的&#xff1f; 补充参考视频 跨域&#xff08;Cross-Origin&#xff09; 这里再说一下跨域的概念吧。 在Web开发中&#xff0c;浏览器限制了从一个不同来源&#xff…
阅读更多...
【C++】415.字符串相加

【C++】415.字符串相加

题目描述&#xff1a; 给定两个字符串形式的非负整数 num1 和num2 &#xff0c;计算它们的和并同样以字符串形式返回。 你不能使用任何內建的用于处理大整数的库&#xff08;比如 BigInteger&#xff09;&#xff0c;也不能直接将输入的字符串转换为整数形式。 示例1&#x…
阅读更多...
XPS虽没流行，但还在使用！在Windows 10中打开XPS文件的最佳方法

XPS虽没流行，但还在使用！在Windows 10中打开XPS文件的最佳方法

当Windows Vista发布时&#xff0c;微软推出了XPS格式&#xff0c;这是PDF的替代品。XPS文件格式并不是什么新鲜事&#xff0c;但从未获得过多大的吸引力。 因此&#xff0c;XPS&#xff08;XML Paper Specification&#xff09;文件是微软对Adobe PDF文件的竞争对手。尽管XPS…
阅读更多...
Kafka三种认证模式，Kafka 安全认证及权限控制详细配置与搭建

Kafka三种认证模式，Kafka 安全认证及权限控制详细配置与搭建

Kafka三种认证模式，Kafka 安全认证及权限控制详细配置与搭建。 Kafka三种认证模式 使用kerberos认证 bootstrap.servers=hadoop01.com:9092,hadoop02.com:9092,hadoop03.com:9092,hadoop04.com:9092 security.
阅读更多...
分布式微服务技术栈-SpringCloud＜Eureka，Ribbon，nacos＞

分布式微服务技术栈-SpringCloud＜Eureka，Ribbon，nacos＞

微服务技术栈 一、微服务 介绍了解1 架构结构案例与 springboot 兼容关系拆分案例拆分服务拆分-服务远程调用 2 eureka注册中心Eureka-提供者与消费者Eureka-eureka原理分析Eureka-搭建eureka服务Eureka-服务注册Eureka-服务发现 3 Ribbon组件 负载均衡Ribbon-负载均衡原理Ribb…
阅读更多...
深入探求：中国精益生产与管理实践的崭新视角

深入探求：中国精益生产与管理实践的崭新视角

经过多方位的了解&#xff0c;比之制造行业上的精益管理上的表现情况&#xff0c;认为目前国内的精益生产精益管理实践仍处于自我认知的水平。目前很多的企业前进的步伐还是主要依据市场经济发展所衍生出来的较为先进的工具运用&#xff0c;其战略性的管理处于局部优化再而达到…
阅读更多...
2.3 如何使用FlinkSQL读取写入到JDBC(MySQL)

2.3 如何使用FlinkSQL读取写入到JDBC(MySQL)

1、JDBC SQL 连接器 FlinkSQL允许使用 JDBC连接器&#xff0c;向任意类型的关系型数据库读取或者写入数据 添加Maven依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-jdbc</artifactId><version>3.1…
阅读更多...
基于RuoYi-Flowable-Plus的若依ruoyi-nbcio支持自定义业务表单流程的集成方法与步骤（一）

基于RuoYi-Flowable-Plus的若依ruoyi-nbcio支持自定义业务表单流程的集成方法与步骤（一）

更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码&#xff1a; https://gitee.com/nbacheng/ruoyi-nbcio 演示地址&#xff1a;RuoYi-Nbcio后台管理系统 由于大家最自定义业务表单的整个集成方法还不熟悉&#xff0c;下面大概介绍一下这个流程与方法。 1、首先…
阅读更多...
顿号在键盘上怎么打？教你4个输入方法！

顿号在键盘上怎么打？教你4个输入方法！

“朋友们&#xff0c;我正在准备一篇期末论文&#xff0c;但是文章里的顿号我一直输入不了。顿号在键盘上应该怎么输入呀&#xff1f;谁能教教我呢&#xff1f;非常感谢&#xff01;” 在使用电脑编辑文档时&#xff0c;我们可能经常需要输入顿号。但有些朋友还不知道顿号在键盘…
阅读更多...
Java 关键字：synchronized详解

Java 关键字：synchronized详解

synchronized详解 基本使用源码解析常见面试题好书推荐 基本使用 Java中的synchronized关键字用于在多线程环境下确保数据同步。它可以用来修饰方法和代码块 当一个线程访问一个对象的synchronized方法或代码块时&#xff0c;其他线程将无法访问该对象的其他synchronized方法或…
阅读更多...
ppt录屏怎么导出来？学会这个，让分享更容易

ppt录屏怎么导出来？学会这个，让分享更容易

ppt已经成为了日常工作与学习中必不可少的工具&#xff0c;而ppt屏幕录制功能&#xff0c;可以方便用户将他人的演讲或视频中的内容记录下来&#xff0c;以便进一步学习与研究。录制ppt演示并将其导出为视频文件&#xff0c;可以帮助我们进行分享&#xff0c;但是很多人不知道p…
阅读更多...
el-upload实现上传文件夹

el-upload实现上传文件夹

背景&#xff1a;如图一所示&#xff0c;最下面有一个黄色上传文件按钮&#xff0c;为手动上传而且上传区域有上传文件和上传文件夹的区分 所以需要在点击了上传文件夹做特殊处理使得el-upload可以上传文件夹 一、template区域 <el-uploadclass"upload-file"dra…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023