2022年亚太杯APMCM数学建模大赛
B题 高速列车的优化设计
原题再现:
2022年4月12日,中国高铁复兴号CR450动车组在开放线上成功实现单车时速435公里,相对速度870公里,创造了高铁动车组列车穿越开放线和隧道速度的世界纪录。新一代标准动车组“复兴号”是中国自主研发的具有完全知识产权的新一代高速列车。它集成了大量国内现代高科技,在牵引、制动、网络、转向架、车轴等关键技术上取得了重要突破。这是中国科技创新的又一重大成果。图1是高速铁路几何结构的简化模型。
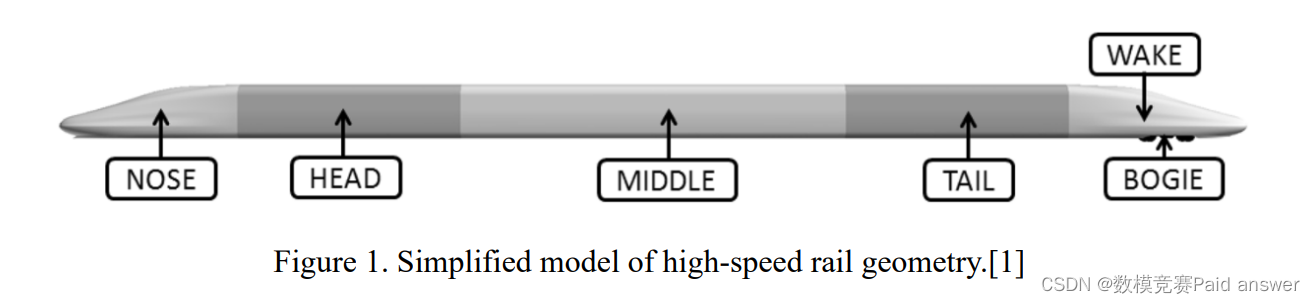
中国高速铁路的车头结构为子弹头,日本高速铁路采用鸭嘴结构。图2显示了四种典型高速铁路头部结构的简化模型,包括TP1、TP2、TP3和TP4。其中,高铁轨头结构的设计主要考虑空气阻力和噪声水平。
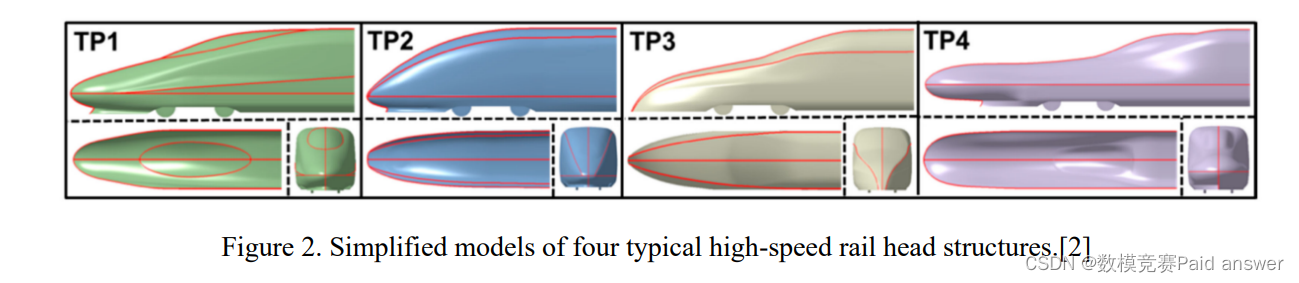
高速铁路弹头的设计过程不仅要以空气动力学为基本原理,还要反复进行仿真和实验。为了实现车头和车身周围的气流、空气动力等相关参数之间的优化方案,可以经过数千次计算和实验进行优化。图3显示了流线型高速轨头结构的不同区域。
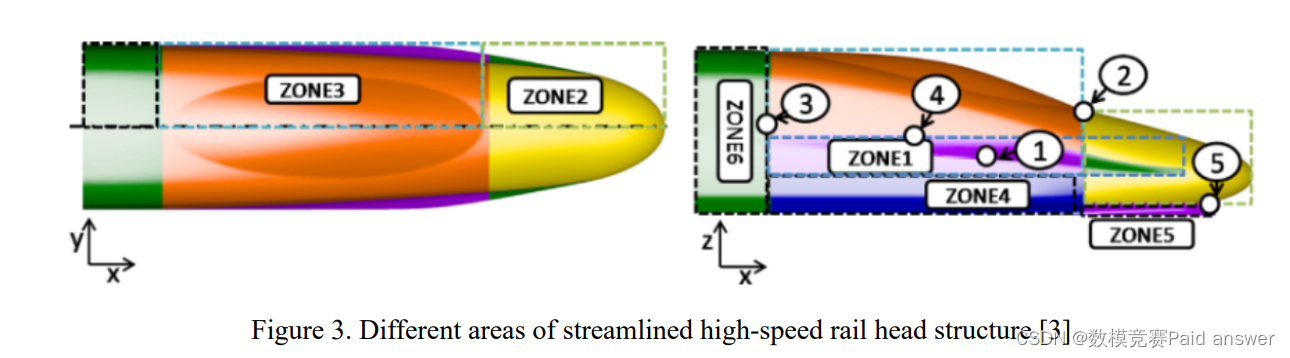
请收集相关数据,建立几个数学模型,并回答以下问题:
问题1:请建立高速铁路空气阻力的数学模型,考虑一般条件和极端天气(如雨、雪、风)下高速铁路几何形状与受力之间的关系,模拟圆锥形和四种典型高速铁路的空气阻力分布,如图2所示,并选择空气阻力最小的最佳高速铁路形状。
问题2:请分析高铁轨头曲线弧度对空气阻力的影响,建立高铁外形优化模型,设计出最佳的高铁外形,使高铁受空气阻力最小,并绘制出优化后的高铁形状草图。
问题3:请建立高铁产生噪声的数学模型,分析锥形和四种典型高铁产生的噪声强度,如图2所示,模拟它们各自的噪声分布,选择产生噪声最小的最佳高铁形状。
问题4:请结合前三个问题的结果,建立高铁形状的综合优化模型,设计出最佳的高铁形状,同时提高高铁列车的速度,降低噪音。绘制高速铁路的形状草图,并给出相应的结构参数。
整体求解过程概述(摘要)
随着计算领域的快速发展,追求高速、低噪声污染的气动外形显得尤为重要。本文建立了相应的数学模型来研究高速铁路的速度域和噪声域,并进行了仿真。
对于问题1,基于标准𝑘 − 𝜀 模型,分别建立了四个初步的高速列车模型,并对通用车头进行了二维受力分析,并利用RWIND风洞软件对四个模型进行了仿真,定义了用于描述的Δ因子,并对每个模型的Δ因子进行了比较,得出TP1是空气阻力最小的最佳高速列车形状。
对于问题2,我们将TP1分为5个部分,采用Pareto搜索方法对其进行优化和微调,并建立了优化的高铁模型。针对问题3,以及许多学者对高速列车噪声污染进行了研究,许多国家也出台了相应的限速规定。基于湍流的物理特性,我们对以85m/s速度行驶的高速列车进行了建模和分析,并得出结论,TP4是产生最小噪声的最佳高速列车形状。
最后,我们结合TP1和TP4的特点,使用多目标粒子群算法设计了一种新的列车,该列车在风洞实验中具有更平衡的力分布,即良好的速度上限和对环境的低噪声,并且与Δ因子相比,新列车的Δ非常好。𝚫TP1=0.0105,𝚫TP4=0.0031,𝚫TPbest=0.0029。比较优化前后的模型可以发现,鼻锥高度减小,鼻锥长度增加,鼻锥变得更光滑;驾驶员室的高度向下调整,流线型的前半部分变得更窄,后半部分的宽度增加。
模型假设:
1.不同高速铁路的材料相同。
2.高铁是直的。
3.风速相同。
4.身体长度相同。
问题分析:
问题1
通过我们对流体连续性原理的分析,本质上流体在流动中的质量守恒,对于理想流体可以得到伯努利方程它是机械能守恒,对于实际流体可以得到泊肃耳定理它是粘性摩擦的存在,这种粘性摩擦会对流体和固体的相对运动产生一种阻力,据此建立空气阻力模型来研究高速铁路的空气阻力。当流体速度非常快时,会产生湍流。在这方面𝑘 − 𝜀 应用该模型求解湍流动能及其耗散率方程。对于四种高速铁路形状,在极端天气(如雨雪)下,我们使用受力分析方法来表示受力关系,对于不同形状的高速铁路,我们使用Blender软件制作了四个高速铁路前端模型,并对这四个模型进行了风洞实验,可以直观地感受到空气对每个部件的阻力,通过比较空气阻力分布来选择空气阻力分布,我们选择了空气阻力最小的高速铁路形状。最终的TP1是空气阻力最小的最佳高速铁路模型。
问题2
在TP1的基础上,基于Pareto搜索过程建立了优化模型,设计出空气阻力最小的最优高铁模型。
问题3
我们首先收集了相关的噪声数据,对各国高速列车(列车)的噪声有了一定的了解,然后得出当车速很快时,波面加速了积聚,使空气摩擦增加,噪声也随之增加。对此,建立了高速列车的外部空气动力学噪声模型,并通过湍流中的空气阻力模型提取每个节点的湍流动能湍流耗散率,从而确定每个节点的声功率。然后将Lighthill-Colle声学类比理论与高速铁路压力分布进行比较,实现了空气动力学噪声仿真。TP4最终被确定为产生最小噪声的高速铁路的最佳形状。
问题4
在第二个问题中Pareto搜索的基础上,我们使用多目标粒子群算法(MOPSO)结合TP1和TP4的特性来找到近似模型,并在风洞中对该模型进行模拟以获得相关数据。结合第三个问题中理论圆锥曲线的模拟值,优化模型𝚫TPbest=0.0029是TP1和TP4中Δ系数最小的(越小越好),与TP1相比降低了72.38%,降低了6.45%,验证了模型的可行性。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
present00=importdata(’ex00_.txt’);
present01=importdata(’ex01_.txt’);
present02=importdata(’ex02_.txt’);
present03=importdata(’ex03_.txt’);
present04=importdata(’ex04_.txt’);
a00=present00(1:300,3:3);
a01=present01(1:300,3:3);
a02=present02(1:300,3:3);
a03=present03(1:300,3:3);
a04=present04(1:300,3:3);
x=present00(1:300,1:1);
deltaY1 = (a01-a00).ˆ2;
deltaY2 = (a02-a00).ˆ2;
deltaY3 = (a03-a00).ˆ2;
deltaY4 = (a04-a00).ˆ2;
k1=sum(deltaY1);
k2=sum(deltaY2);
k3=sum(deltaY3);
k4=sum(deltaY4);
\begin{tikzpicture}
\draw[->](0,0.1)arc(165:120:5 and 3);
\draw[->](0,-0.3)arc(165:120:5 and 3);
\draw[->](0,-0.5)arc(165:120:5 and 3);
\draw[->](0,-0.7)arc(165:120:5 and 3);
\draw[->](0,-0.1)arc(165:120:5 and 3) ;
\draw[->](0,0.3)arc(165:120:5 and 3);
\draw[rotate around={93:(1.8,1.42)}](1.8,1.3) ellipse(0.5 and 0.3);
\draw[rotate around={-45:(0.4,-0.2)}](0,0) ellipse(0.3 and 0.15);
\end{tikzpicture}
\begin{tikzpicture}
\draw(0,0)arc(80:20:5 and 3);
\draw(0,1)arc(80:20:5 and 3);
\draw(0,-3)--(4,-3);
\draw(0.5,-3)--(0.5,-0.1);
\draw(2.8,-0.9)--(2.8,-3);
\draw(0.6,0.41) ellipse(0.2 and 0.49);
\draw(0.4,0.45) ellipse(0.2 and 0.48);
\draw[rotate around={-45:(3.2,-0.75)}](3.2,-0.75) ellipse(0.15 and 0.38);
\draw(2.5,-0.75)arc(149:100:0.8 and 1.4);
\node[left]at(0.5,-2){$h_{1}$};
\node[left]at(2.8,-2){$h_{2}$};
\node[above]at(0.5,1){$a_{1}b_{1}$};
\draw[->](-0.5,0.45)--(0.2,0.45);
\draw[->](3.8,-1.4)--(3.3,-0.9);
\node[below]at(3.8,-1.4){$p_{2}S_{2}$};
\node[above]at(-0.2,0.45){$p_{1}S_{1}$};
\node[above]at(3.2,-0.2){$a_{2}$};
\node[above]at(3.6,-0.6){$b_{2}$};
\end{tikzpicture}
\begin{tikzpicture}
\draw(2,2) ellipse(1 and 3);
\draw(2,2)ellipse(0.8 and 2.5);
\draw(10,2) ellipse(1 and 3);
\draw(10,2) ellipse(0.8 and 2.5);
\draw(2,-1)--(10,-1);
\draw(2,5)--(10,5);
\draw(2,-0.5)--(10,-0.5);
\draw(2,4.5)--(10,4.5);
\node[above]at (2,5){$a$};
\node[above]at (10,5){$b$};
\draw(2,-1.1)--(2,-2);
\draw(10,-1.1)--(10,-2);
\draw[->](6,-1.5)--(2,-1.5);
\draw[->](6.3,-1.5)--(10,-1.5);
\node[right]at(6,-1.5){$l$};
\draw[->](7,5.2)--(5,5.2);
\draw(1.9,5)--(0.1,5);
\draw(10,4.5)--(0.9,4.5);
\draw[->](5,4.3)--(7,4.3);
\draw(0.3,2)--(1.8,2);
\draw[->](2.1,2)--(4,2);
\draw(4.2,2)--(8,2);
\draw(8.2,2)--(10,2);
\draw(10.2,2)--(12,2);
\draw[->](0.5,3.8)--(0.5,5);
\node[below]at(0.5,3.8){$r+dr$};
\draw[->](0.5,3.3)--(0.5,2);
\draw[->](1,3.3)--(1,4.5);
\node[below]at(1,3.3){$r$};
\draw[->](1,3)--(1,2);
\node[below]at(10.5,2){$p_{b}$};
\node[above]at(6,5.2){$f_{r+dr}$};
\node[below]at(6,4.3){$f_{r}$};
\node[below]at(0.5,2){$P_{a}$};
\node[above]at(4,2){$v$};
\end{tikzpicture}