文章目录
- 单只股票买卖
- 多次买卖单只股票
- 最多两次买卖股票
- 最多买k次
- 含冷静期
- 含手续费
单只股票买卖
买卖股票的最佳时机
关键思路:找到一个值,他与之后的最大值之差最大。
用minprice记录最小的值,用maxprofit记录最大的收益。
想清楚一个点:
- 更新最小值时,影响最大收益吗?
- 不会影响,因为每个收益都是需要根据minprice后续的最大值
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<=1) return 0;
int n = prices.length;
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
for(int i = 0 ; i < n ;i++ ){
minprice =Math.min(minprice, prices[i]);
maxprofit = Math.max(prices[i] -minprice,maxprofit);
}
return maxprofit;
}
}
多次买卖单只股票
买卖股票的最佳时机 II
profitBuy 用于记录已购买股票后的最大利润,而 profitNOBuy 用于记录未购买股票时的最大利润。在一个循环中,它逐步计算了每一天的最佳策略,然后返回最后一天的最大利润。
profitBuy[i]表示在第i天持有股票时的最大利润,它等于在第i-1天继续持有股票或在第i-1天卖出股票后买入的最大值。profitNOBuy[i]表示在第i天没有持有股票时的最大利润,它等于在第i-1天继续观望不购买股票或在第i-1天购买股票后卖出的最大值。
在遍历结束后,函数返回两种情况的最大值,即最大利润。用动态规划的方法来解决买卖股票的问题,确保在每一天都选择最优的策略以获得最大的利润。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int profitBuy[] = new int[n]; // 用于记录已购买股票后的最大利润
int profitNOBuy[] = new int[n]; // 用于记录未购买股票时的最大利润
profitBuy[0] = -prices[0]; // 初始化第一天已购买的情况,初始资金为负的第一天股票价格
profitNOBuy[0] = 0; // 初始化第一天未购买股票的情况,初始资金为0
for (int i = 1; i < n; i++) {
// 更新已购买股票后的最大利润,考虑继续持有或卖出的情况
profitBuy[i] = Math.max(profitBuy[i - 1], profitNOBuy[i - 1] - prices[i]);
// 更新未购买股票时的最大利润,考虑继续观望或购买的情况
profitNOBuy[i] = Math.max(profitNOBuy[i - 1], profitBuy[i - 1] + prices[i]);
}
// 最终返回最后一天的两种情况的最大值,即最大利润
return Math.max(profitBuy[n - 1], profitNOBuy[n - 1]);
}
}
最多两次买卖股票
123. 买卖股票的最佳时机 III
- 首先,定义了四个变量:
minprice,maxprofit,minprice2,和maxprofit2,它们用来存储在遍历价格数组过程中的一些重要信息。 - 通过循环遍历价格数组
prices,其中i表示当前的天数。 minprice用来记录在第i天之前的最低股票价格。在循循环过程中,不断更新minprice为当前价格prices[i]和minprice之间的较小值。maxprofit用来记录在第i天卖出股票时的最大利润。利润计算为当前价格prices[i]减去之前的最低价格minprice,并且与之前的最大利润maxprofit比较,取较大值。minprice2用来记录在第i天之前的最低股票价格,考虑到第二次交易。这里minprice2考虑了第一次交易的收益maxprofit,即prices[i] - maxprofit,因为在第一次交易中,你已经卖出了一次股票,所以要减去第一次交易的利润。maxprofit2用来记录在第i天卖出股票时的最大利润,考虑第二次交易。利润计算为当前价格prices[i]减去之前的最低价格minprice2,并与之前的最大利润maxprofit2比较,取较大值。- 最后,返回
Math.max(maxprofit2, maxprofit),因为你要最大化两次交易的总利润。
这个算法的关键在于动态地维护四个变量,以确保在每一天都考虑了两次交易的情况,并计算出最大利润。
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
if(n<=1) return 0;
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
int minprice2 = Integer.MAX_VALUE;
int maxprofit2 = 0;
for(int i = 0 ; i < n ;i++ ){
minprice = Math.min(minprice, prices[i]);
minprice2 = Math.min(minprice2 , prices[i] - maxprofit);
maxprofit = Math.max(prices[i] -minprice,maxprofit);
maxprofit2 = Math.max(maxprofit2 , prices[i] - minprice2);
}
return Math.max(maxprofit2,maxprofit);
}
}
最多买k次
188. 买卖股票的最佳时机 IV
把k想象成2即可,按照两次的思路
class Solution {
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if(n<=1) return 0;
int minprice[] = new int[k];
int maxprofit[] = new int[k];
for(int i=0;i<k;i++){
minprice[i] = Integer.MAX_VALUE;
maxprofit[i] = 0;
}
for(int i = 0 ; i < n ;i++ ){
minprice[0] = Math.min(minprice[0], prices[i]);
maxprofit[0] = Math.max(prices[i] -minprice[0],maxprofit[0]);
for(int j=1;j<k;j++){
minprice[j] = Math.min(minprice[j] , prices[i] - maxprofit[j-1]);
maxprofit[j] = Math.max(maxprofit[j] , prices[i] - minprice[j]);
}
}
return maxprofit[k-1];
}
}
含冷静期
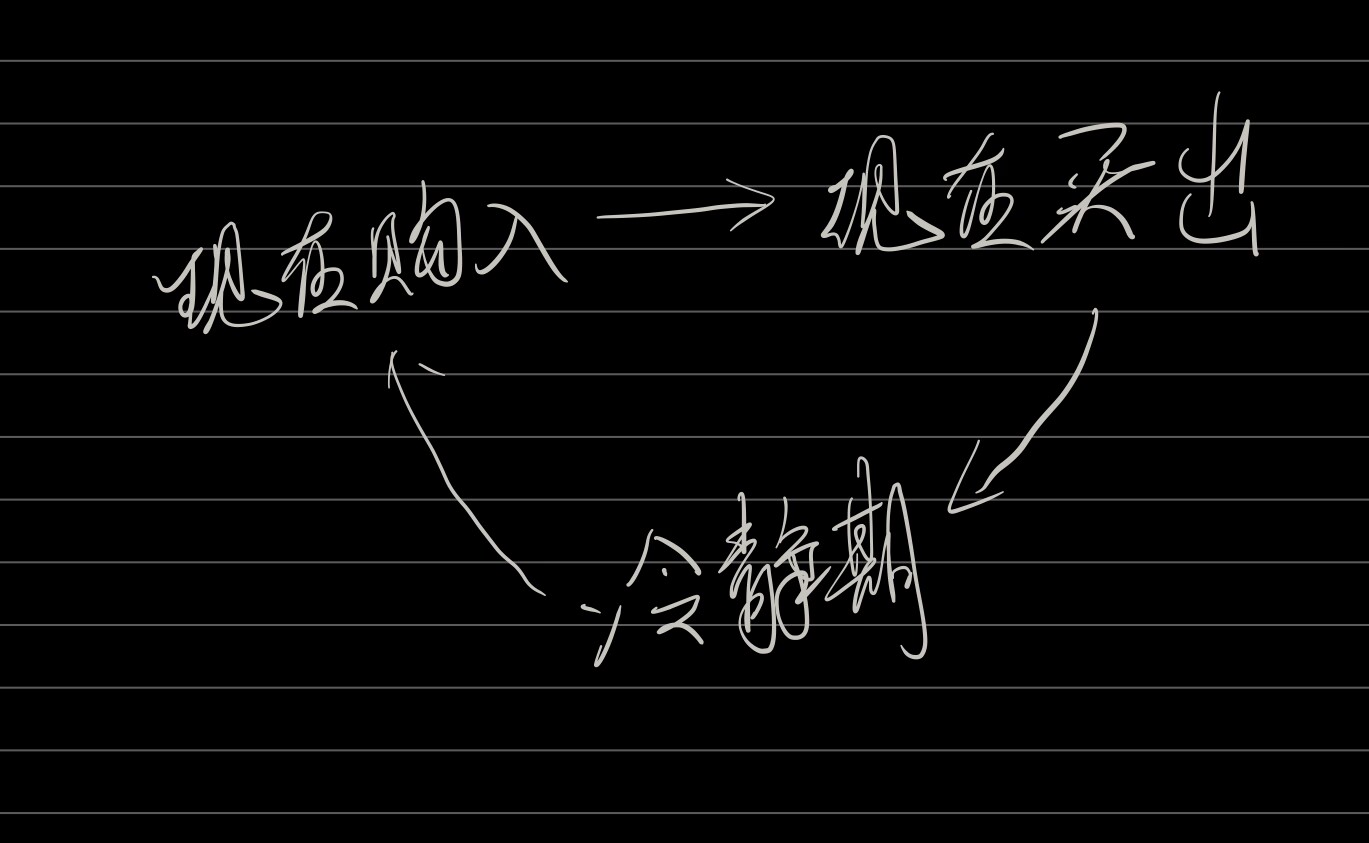
309. 买卖股票的最佳时机含冷冻期
状态转移图
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
if(n<=1) return 0;
int dpNoBuy[] = new int[n];
int dpBuy[] = new int[n];
int dpCd[] = new int[n];
dpNoBuy[0] = -prices[0];
dpBuy[0] = 0;
dpCd[0] = 0;
for (int i = 1; i < n; i ++) {
dpNoBuy[i] = Math.max(dpCd[i-1] - prices[i],dpNoBuy[i-1]);
dpBuy[i] = Math.max(dpNoBuy[i-1] + prices[i],dpBuy[i-1]);
dpCd[i] = Math.max(dpCd[i-1],dpBuy[i-1]);
}
return Math.max(Math.max(dpNoBuy[n-1],dpCd[n-1]),dpBuy[n-1]);
}
}
含手续费
714. 买卖股票的最佳时机含手续费
两个状态转换即可
class Solution {
public int maxProfit(int[] prices, int fee)
{
int n = prices.length;
if(n<=1) return 0;
int buy[] = new int[n];
int sell[] = new int[n];
buy[0] = -prices[0];
sell[0] = 0;
for(int i = 1;i<n;i++){
buy[i] = Math.max(buy[i-1],sell[i-1]-prices[i]);
sell[i] = Math.max(sell[i-1],buy[i]+prices[i]-fee);
}
return Math.max(buy[n-1],sell[n-1]);
}
}