b站视频

为什么使用激活函数

没有激活函数，无论怎么调整权重和偏差输出值仍为线性，但是真实世界大多数系统是非线性的
只有神经网络中包含至少一层隐藏层和足够的神经元，利用非线性激活函数可以模拟任何复杂的连续函数

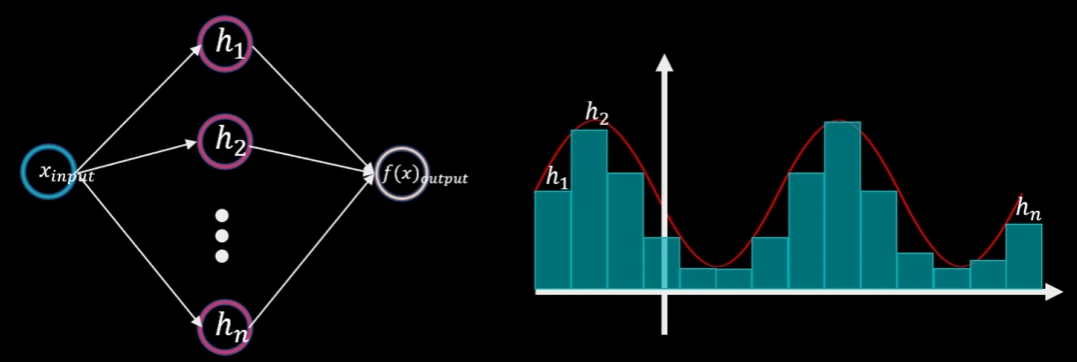
激活函数的选择

sigmoid

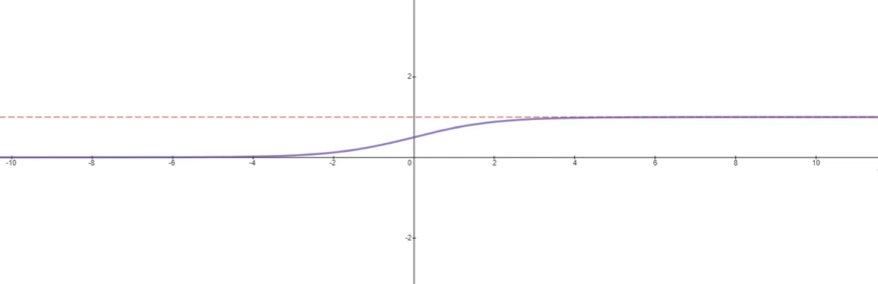
特点

1. 其输出值落于 0 1 连续区间
2. 在输入值从横坐标左侧移动到右侧的过程中，其输出值呈现从平缓到加速再到平缓的特点
3. Sigmoid 函数的导数值落于 0 0 ． 25 的连续区间

局限性

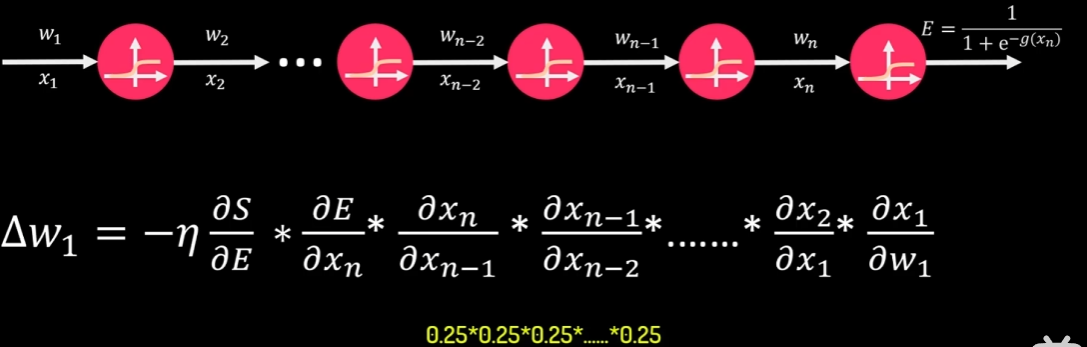
• 多个0.25相乘后，会严重影响最终的权重调整幅度，第一层的初始权重之后很难通过，反向传播再变化，成为梯度消失
• 在进行指数计算时需要消耗较的算力资源，故不常使用

tanh

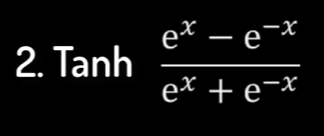
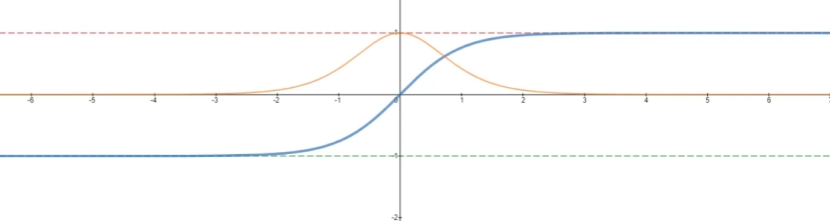
特点

1. 其输出值落于 -1，1 连续区间
2. 函数的导数值落于 0，1的连续区间
   tanh 能够相对环节梯度消失的问题
   

ReLU(Rectified Linear Unit)

(隐藏层的默认推荐激活函数)

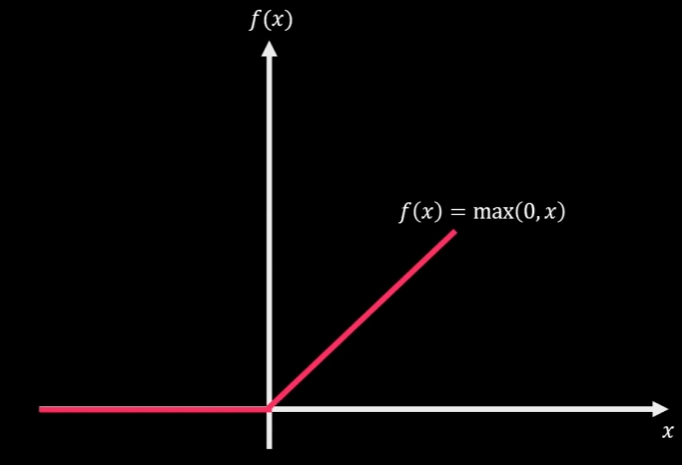
它是一个非线性函数，其在 〉 0 时展示的线性特征，能很好的解决梯度消失的问题，且相较于前两者可以带来更高效的计算
整体的非线性可以在神经网络中拟台任何复杂的连续函数

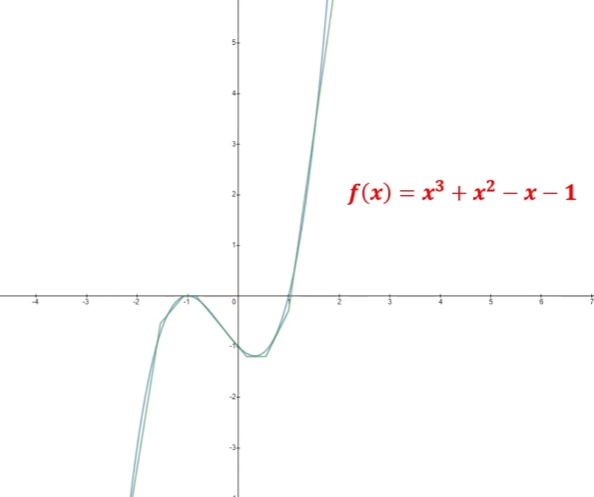
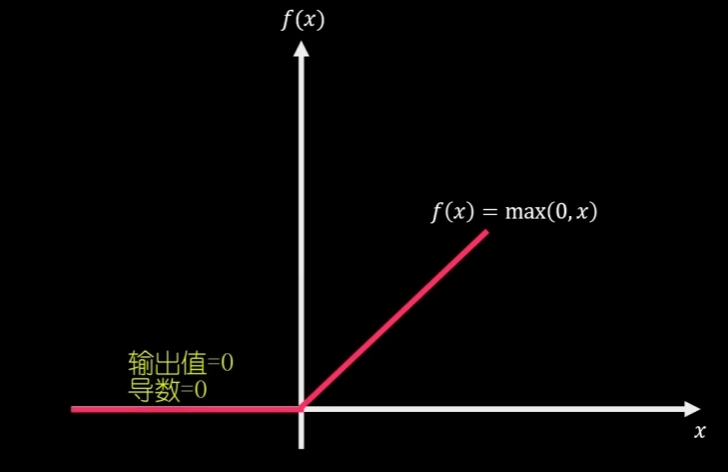
输入为负数时，输出值和导数均为0，此时该神经元处于熄灭状态

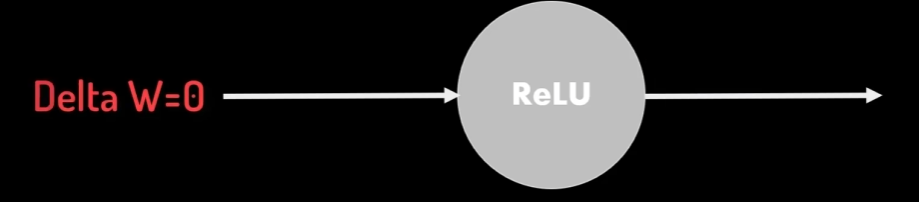
且在逆向参数调整过程中不产生梯度调整值

Leaky ReLU（ ReLU 函数的变形体）

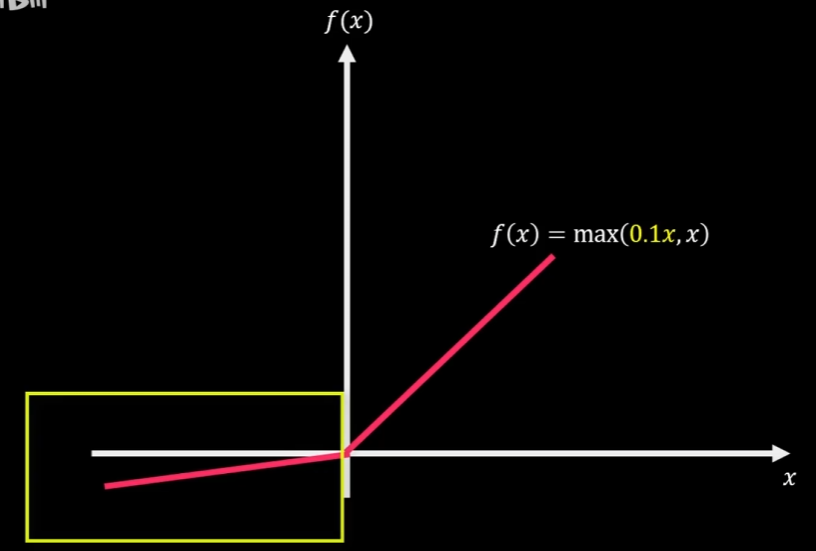
再负数区间内添加较小斜率的线性部分，使负数区域内也能产生梯度调整值

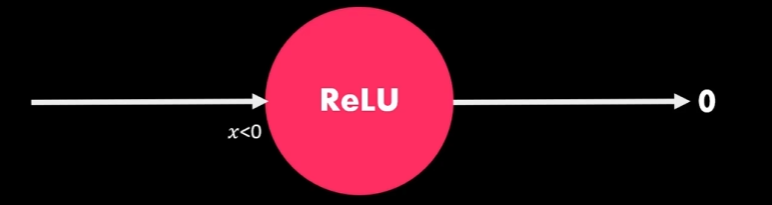
解决神经元的熄灭问题

隐藏层的选择顺序

输出层的激活函数以业务要求为导向

二分类问题

判断是否是猫

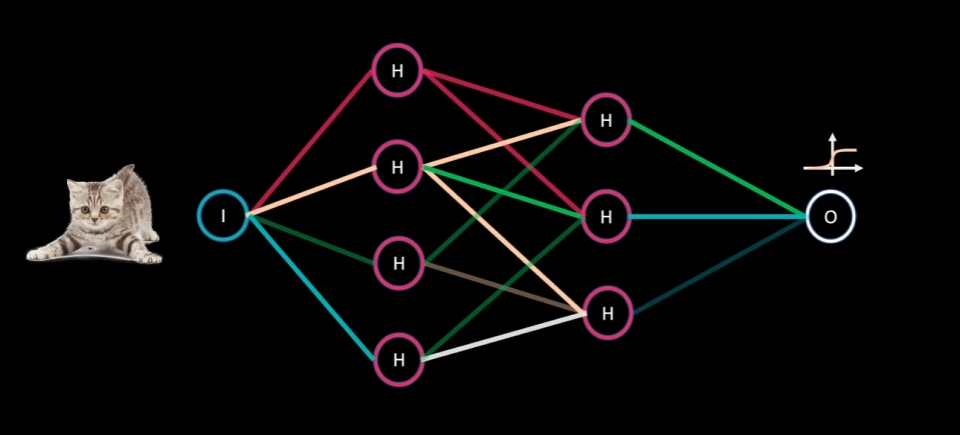
我们可以用 Sigmoi d 丞数返回是猫的概率作为最终输出值

多分类问题

希望返回每个动物的概率

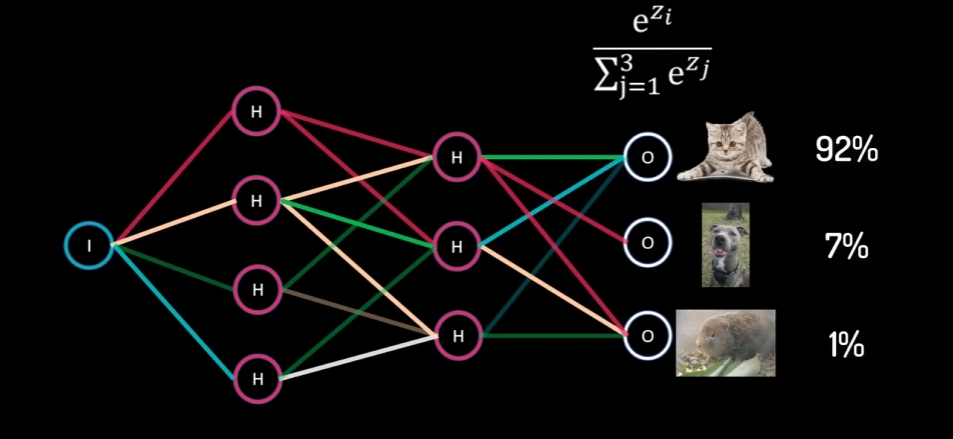
可以使用 SoftMax 函数吗，概率总和为1

多标签问题

某样本可以同时属于多个类别

这里也可以用 sigmoid 函数每个类的概率

线性回归问题

要预测绝对的数值时，比如身高体重 GDP 投资额等
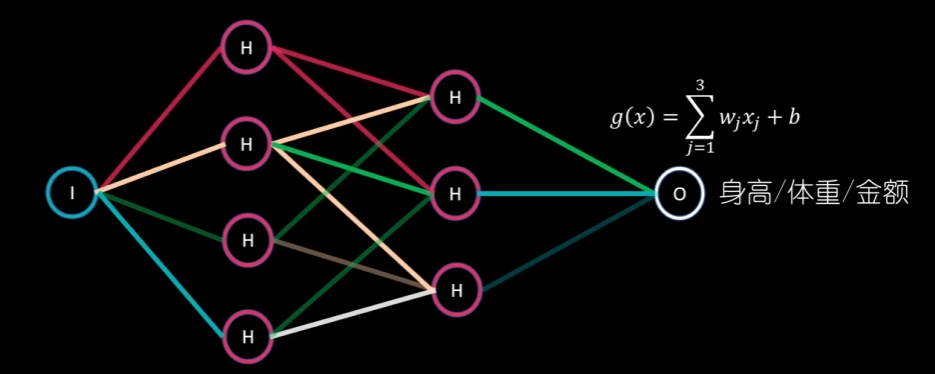那么最后就可以直接使用线性函数作为激活函数