项目开发使用vue-pdf,单页情况预览正常，多页vue-pdf预览异常，第一次预览时，会先弹出异常模态窗口，关闭模态窗口，pdf又是正常显示，报错信息及异常截图如下：

报错信息
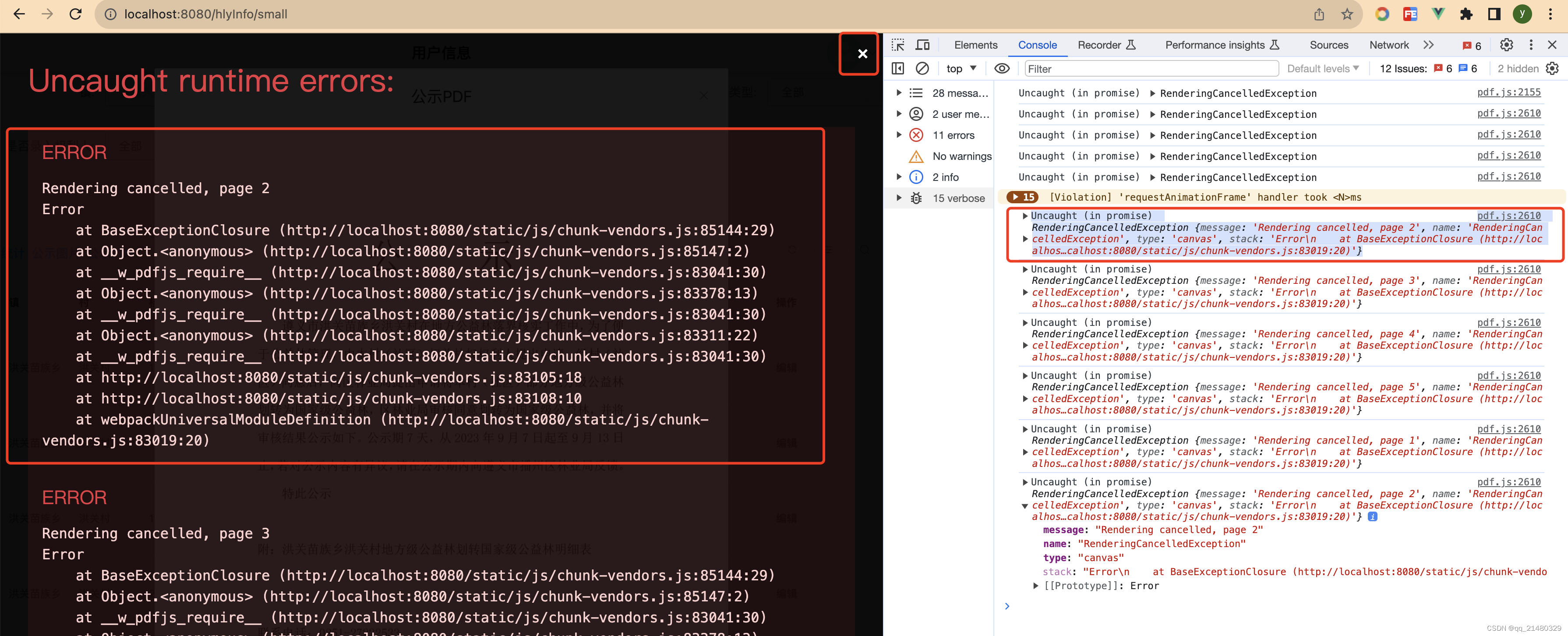
Rendering cancelled, page 1 Error at BaseExceptionClosure xxx

pdf.js:2610 Uncaught (in promise) RenderingCancelledException {message: 'Rendering cancelled, page 2', name: 'RenderingCancelledException', type: 'canvas', stack: 'Error\n    at BaseExceptionClosure (http://localhos…calhost:8080/static/js/chunk-vendors.js:83019:20)'}

异常截图，点击右上角关闭X，pdf是正常预览，再次打开后也能正常预览，仅第一次打开预览有异常。

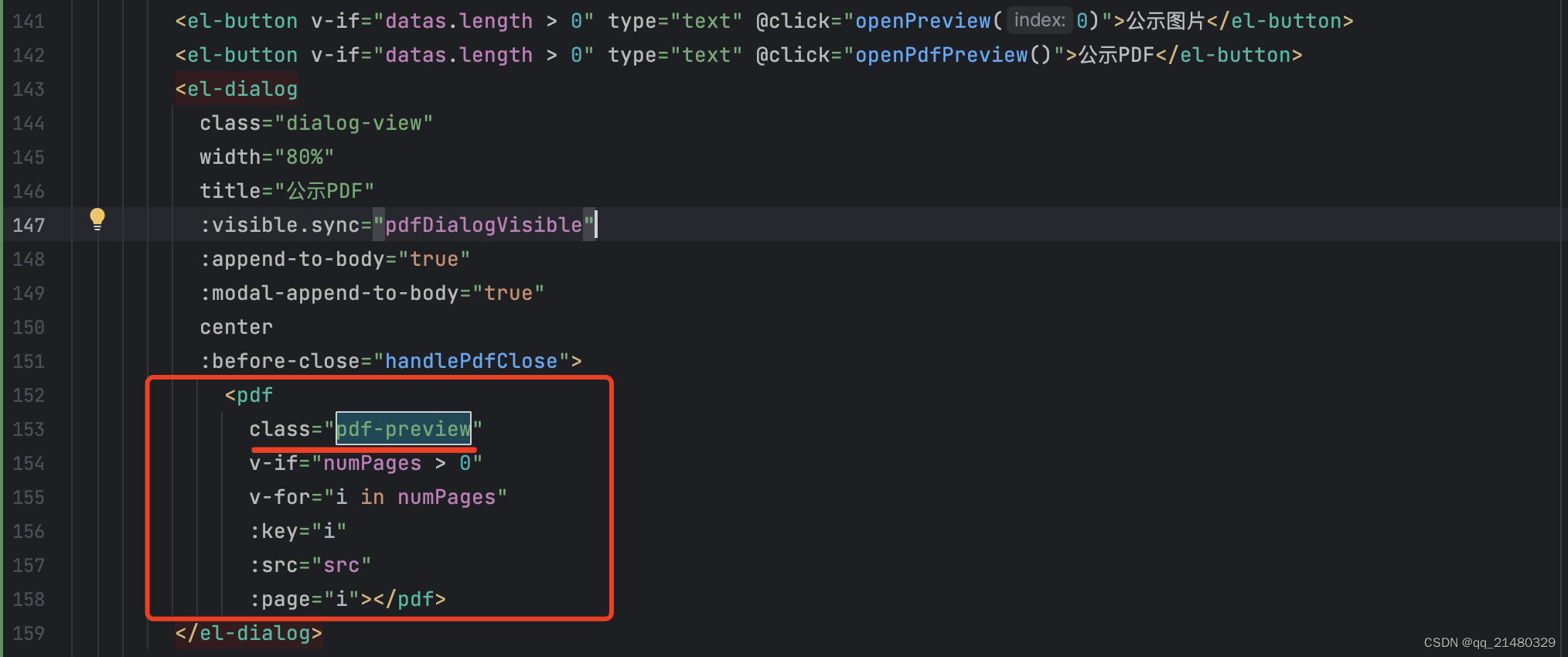
1.vue-pdf预览源码
配置相应的参数即可：-Djava.net.preferIPv4Stack=true

        <el-button v-if="datas.length > 0" type="text" @click="openPdfPreview()">公示PDF</el-button>
        <el-dialog
          class="dialog-view"
          width="80%"
          title="公示PDF"
          :visible.sync="pdfDialogVisible"
          :append-to-body="true"
          :modal-append-to-body="true"
          center
          :before-close="handlePdfClose">
            <pdf
              class="pdf-preview"
              v-if="numPages > 0"
              v-for="i in numPages"
              :key="i"
              :src="src"
              :page="i"></pdf>
        </el-dialog>

	// 预览关键代码
    openPdfPreview() {
      if (!this.pdfSrc) {
        this.$message.warning('未上传pdf文件')
        return
      }

      this.pdfDialogVisible = true
     // pdfSrc     url地址
      let loadingTask = pdf.createLoadingTask(this.pdfSrc, {withCredentials: false});
      loadingTask.promise
        .then((pdf) => {
        // 计算总页数
          this.numPages = pdf.numPages;
        })
        .catch((err) => {
          console.error("pdf 加载失败", err);
        });

    },

2.预览异常解决方案
导致这个问题的主要原因是pdf预览组件，未设置高度，仅需要给pdf组件设置一个高度即可解决，设置高度后，再次预览，一切正常，代码如下：

  .pdf-preview {
    width: 60%;
    //flex: 1;
    //display: none;
    height: 100vh;
    margin: 0 auto;
  }

.pdf-preview canvas {
  height: 100% !important;
}

3.pdf预览显示不完整，比如字体太大，需要缩放等
a.优化代码，加入缩放处理逻辑，优点能动态调整缩放
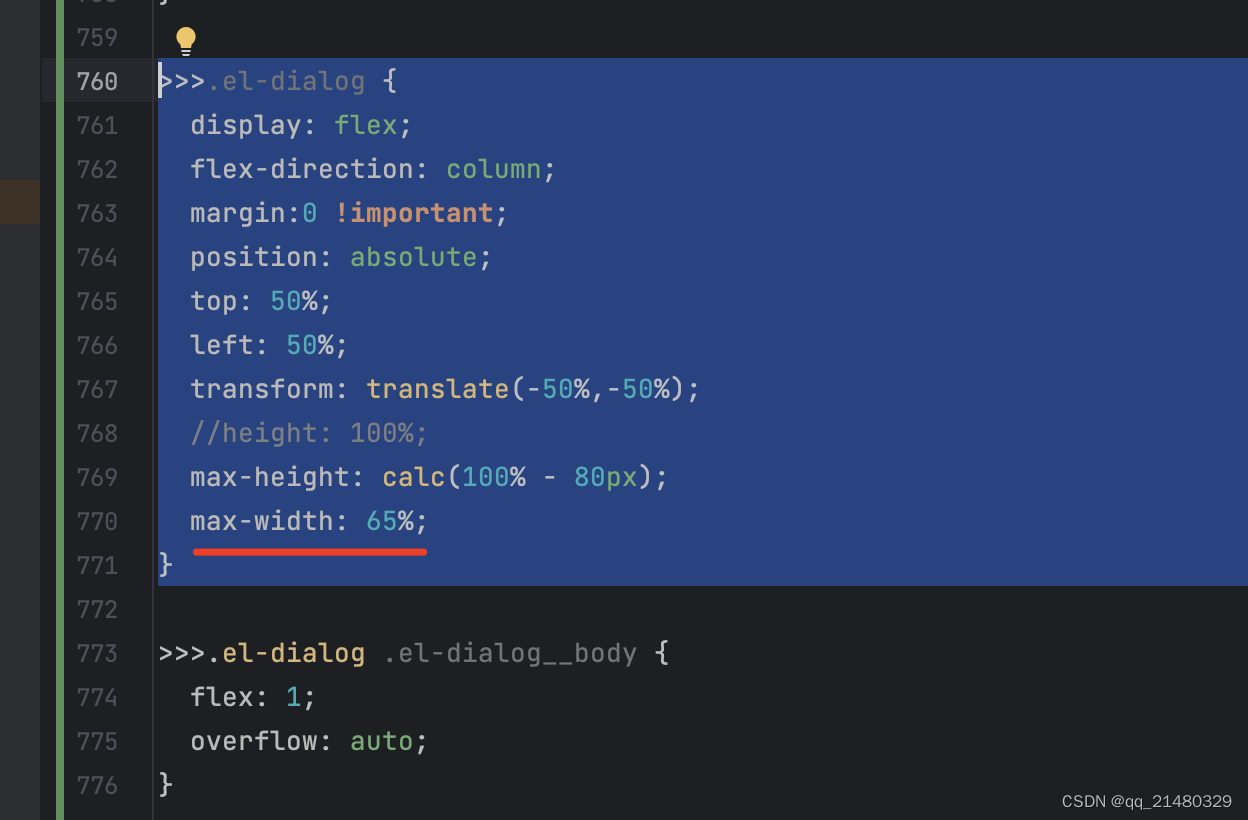
b.修改父容器宽度，会相应缩放pdf的大小，缺点不能动态调整缩放

>>>.el-dialog {
  display: flex;
  flex-direction: column;
  margin:0 !important;
  position: absolute;
  top: 50%;
  left: 50%;
  transform: translate(-50%,-50%);
  //height: 100%;
  max-height: calc(100% - 80px);
  max-width: 65%;
}

4.相关大数据学习demo地址:
https://github.com/carteryh/big-data