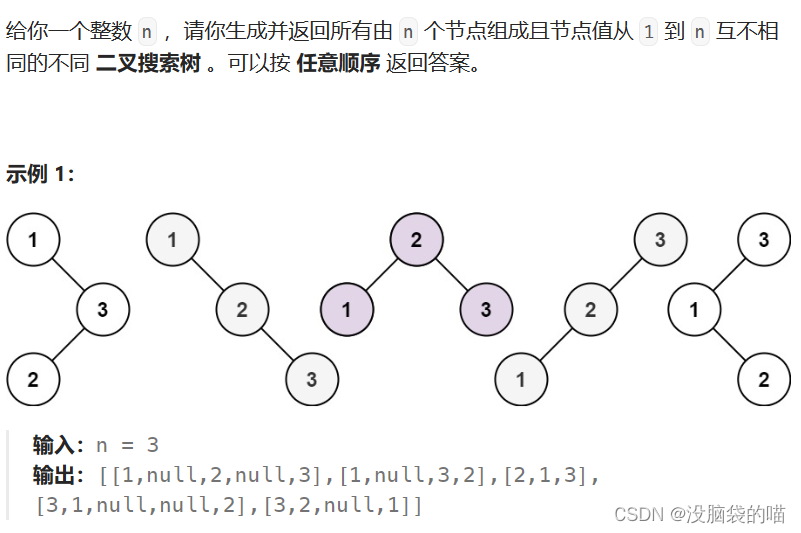
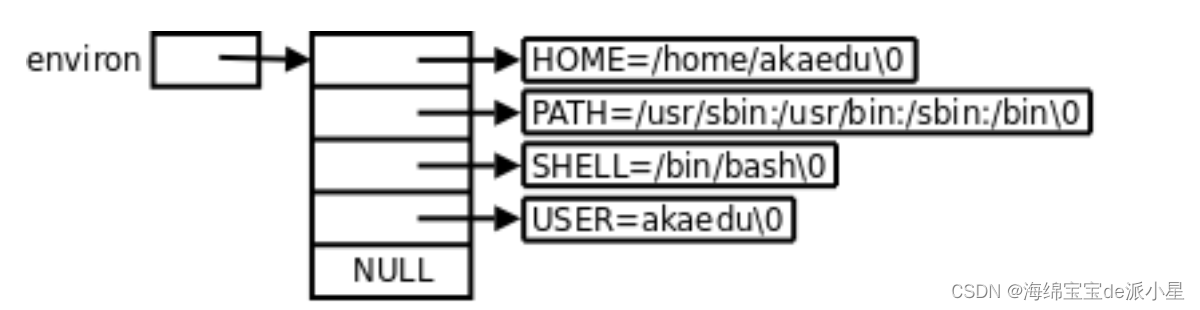
一、什么是聚类分析
1.1概述
- 无指导的,数据集中类别未知
- 类的特征:
- 类不是事先给定的,而是根据数据的相似性、距离划分的
- 聚类的数目和结构都没有事先假定。
- 挖掘有价值的客户:
- 找到客户的黄金客户
- ATM的安装位置
1.2区别·

二、距离和相似系数
2.1概述
- 原则: 组内数据有较高相似度、不同组数据不相似
- 相似性的度量(统计学角度):
- Q型聚类:对样本聚类(行聚类)
- R型聚类:对变量聚类(列聚类)

2.2Q型聚类(样本聚类、行聚类)

1.样本资料矩阵:

2.定义距离的准则:
3.变量的类型
- 间隔尺度变量(数值型变量):可加可比
- 有序尺度变量(叙述型变量):不可加可比
- 名义尺度变量(名义型变量):不可加不可比
4.间隔尺度变量(数值型变量)
缺点:数据集中存在变量取值范围相差十分悬殊,会造成大数吃小数现象。
数值与指标量纲有关
度量值的标准化:
- 将初始测量值转换为无单位变量。
- 常用零均值规范化

特例:比例数值变量
5.有序尺度变量
- 只可以不可加:比如各种排名、等级
- 步骤

6.名义尺度变量(符号变量)
-
两种类型
- 二元变量:
- 只有两个取值变量:如男女、开关、01
- 名义变量:
- 二元变量推广:如颜色变量(R,G,B)
- 二元变量:
-
二元变量计算:
-
差异矩阵法:

-
恒定的相似度
- 对称的二元变量:取值01内容同等价值、相同权值
- 如:男女
- 简单匹配系数
- 取值不一样(01或10)的个数在所有变量的比重
- 对称的二元变量:取值01内容同等价值、相同权值
-
非恒定的相似度
- 非对称二元变量:取值01内容重要程度不同
- 如:病毒阴阳性
- Jaccard相关系数
- 取值不一样(01或10)的个数在所有变量(除去取值为00)的比重
- 非对称二元变量:取值01内容重要程度不同
- 相似度系数例子(小题计算):

- 名义变量计算(最常用):


-
7.混合数据类型
- 现实数据库中包含多类型的数据
- 如何计算?
- 将变量按类型分组,对每种类型的变量单独聚类分析,但实际中,往往不可行。
- 将所有的变量一起处理,只进行一次聚类分析。
- 相似度计算



2.3R型聚类(变量聚类、列聚类)
-
相似系数:
- 夹角余弦
- 相关系数
-
夹角余弦
- 值越大越好

-
变量间相似系数

-
相似系数

-
相似矩阵
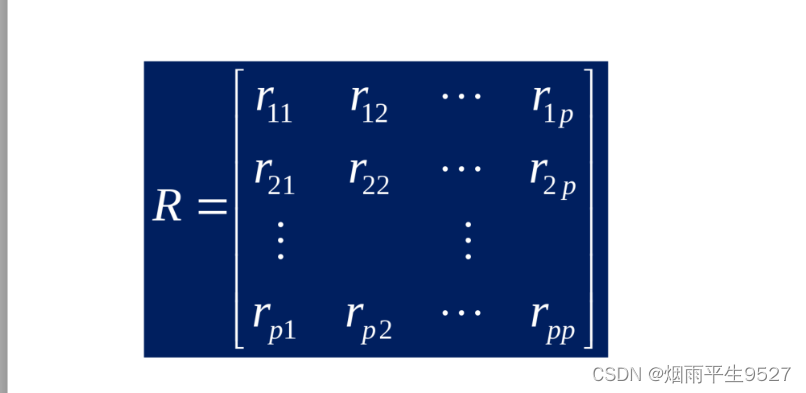
三、 类的定义和类间距离
3.1类的定义
- 定义1:任意元素
,间距离
满足:
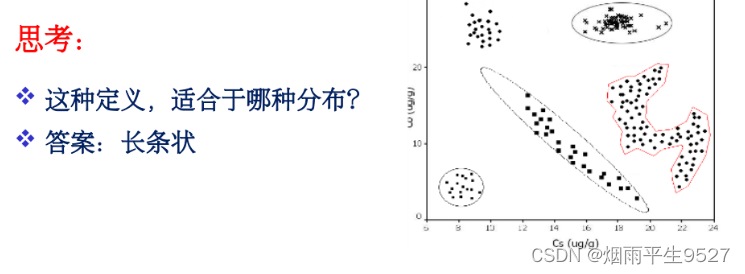
- 适合:团簇状
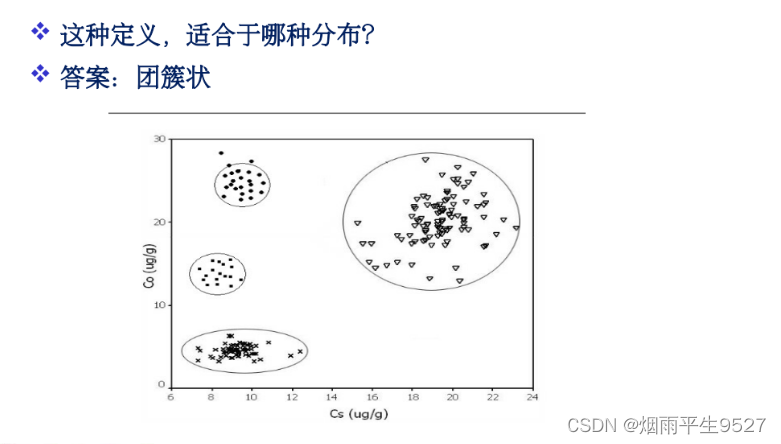
- 定义2:任意元素
,间距离
满足
(类内平均距离)
- 适合:团簇状
- 定义3:对于任意元素
,存在
使得其满足
(不要求任意两个元素)
- 适合:长条状
3.2类间距离
-
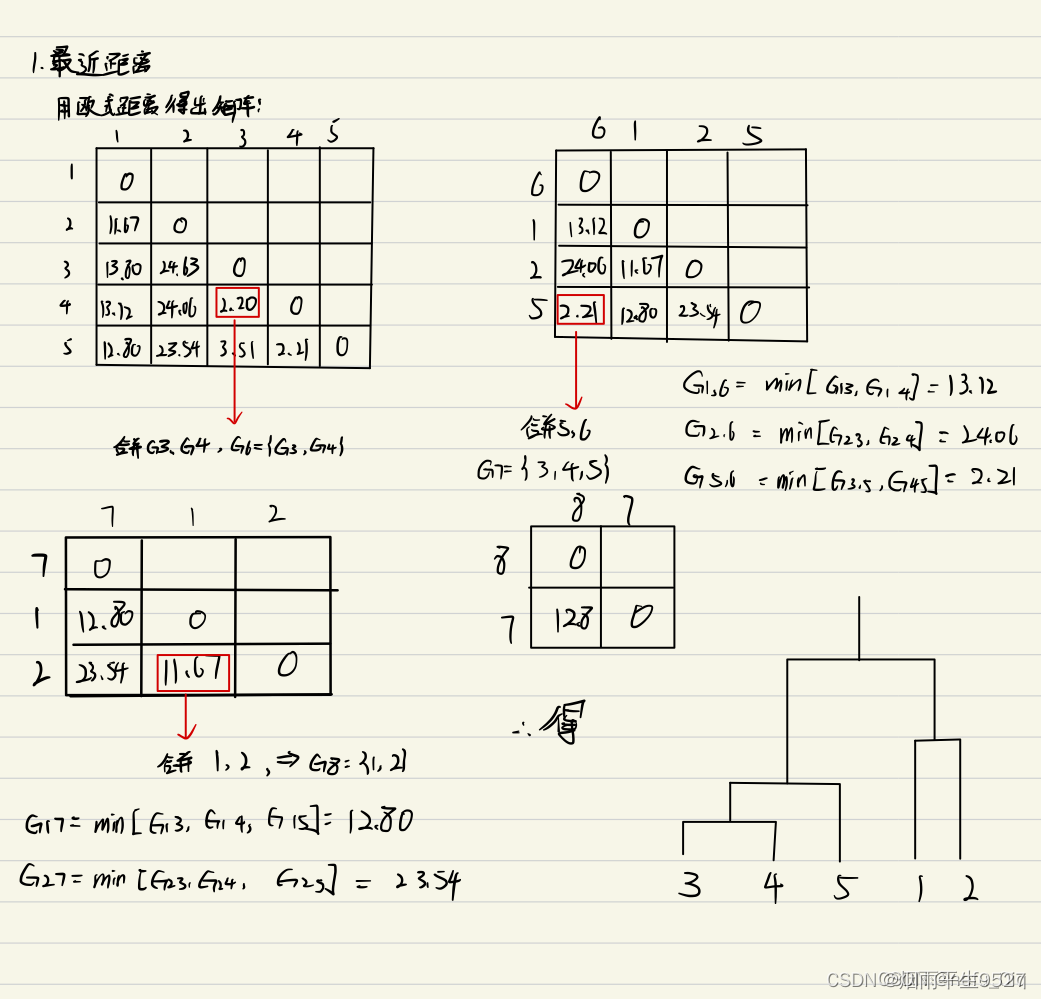
最近距离
-
与
最近距离为
-
是
和
,合并得到的
-
实际中不多见,避免极大值影响

-
例子
-
计算类间距离,然后将最小的两个进行合并

-
-
-
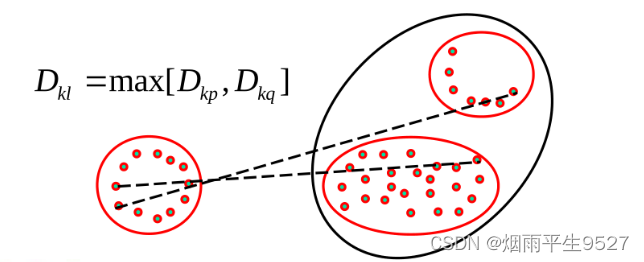
- 最远距离
与
最远距离为
是
和
,合并得到的
-
可能被极大值扭曲,删除后再聚类
-
例题:与上面的类似,每次选取距离最小的,合并的时候取的是max
-
平均距离
-
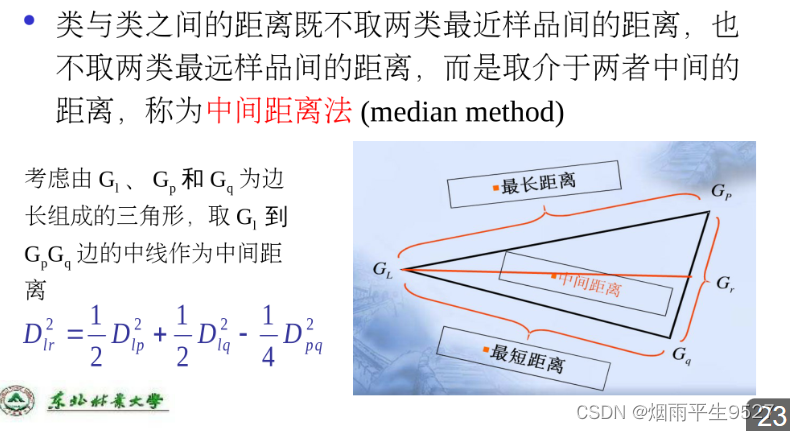
- 中间距离
- 重心距离
-
一个类空间的位置用重心表示,两个类重心之间距离为二者的距离

-
对异常值不敏感,结果能稳定
-
四、基于划分的聚类方法
4.1划分方法
- 将n个对象划分成k类,且满足:
- 每个聚类内至少包含一个对象
- 每个对象必须属于一个类(模糊划分计划可以放宽要求)
- 划分方法:
- k-均值:每个聚类用该聚类中对象的平均值表示
- k-中心点:每个聚类用接近聚类重心的一个对象(真实存在的点)表示
4.2k-均值聚类算法
-
用类均值表示
-
不适合处理离散型属性,适合处理连续型属性
-
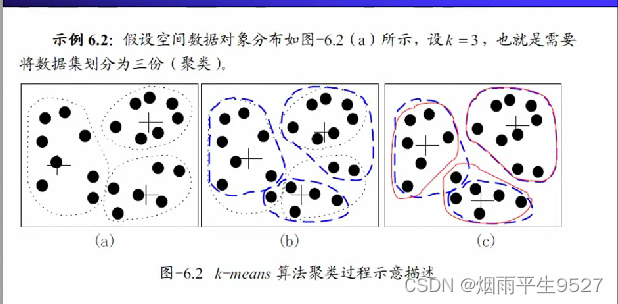
算法流程:

- 选取聚类中心:随机从n个数据选择k个对象作为初始聚类中心
- 对剩余的每个对象,根据各个聚类中心的距离,将其赋给最近的聚类。
- 重新计算每个聚类的平均值(中心)
- 不断重复,直到准则函数收敛(减小)
- 收敛准则函数:误差平方和最小

-
缺点:
-
局部最优,不是全局最优
-
结果与k的取值有关
-
不适合发现大小很不相同的簇、凹状的簇
*![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AwfktfUP-1641719199744)(/uploads/upload_98816f0f833feeb2da5536e0c31765d5.png =400x)]](https://img-blog.csdnimg.cn/1fec809c19684e9988326cf8ab99721c.png)
-
只有在簇的平均值被定义的情况下才能使用,不适合有类属性的数据。
-
对噪声、异常点敏感。
-
-
示意图例子:
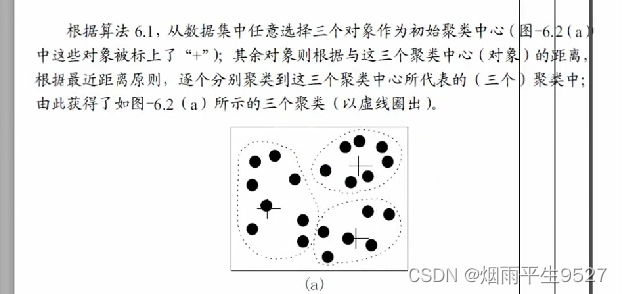
-

4.3k-中心点聚类算法
- k-中心点与k-均值算法区别
簇中心 评价准则 k-均值 簇中对象均值(可以是虚点) 误差平方和 k-中心点 接近簇中心的一个对象表示(实际存在的点) 绝对误差
- 基本策略
- 随意选择一个代表对象作为中心点,将剩余对象按最小距离划分进簇中。
- 重复利用非中心对象代替中心对象,若改善聚类的整体距离,则进行替代。
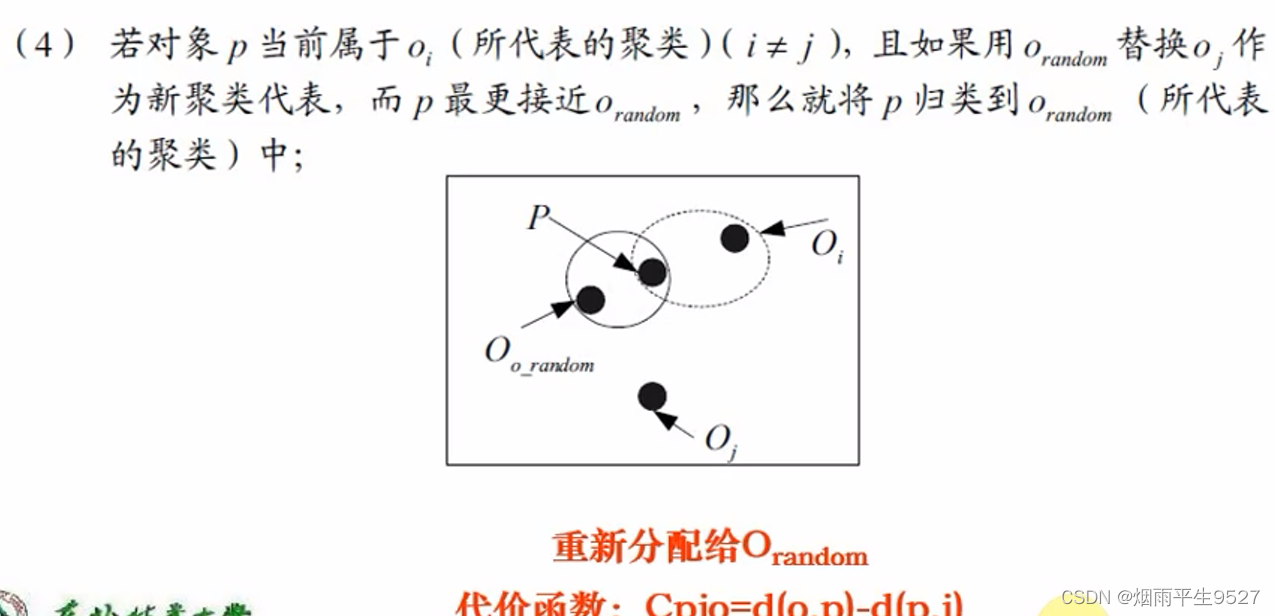
- 用代价函数进行估算质量:
- 替代的四种情况
- 如何判断非代表对象
是否能替代当前代表对象
,需要对每个非中心点P考虑
- 替换的总代价:
- 若总代价为负,则可以替代
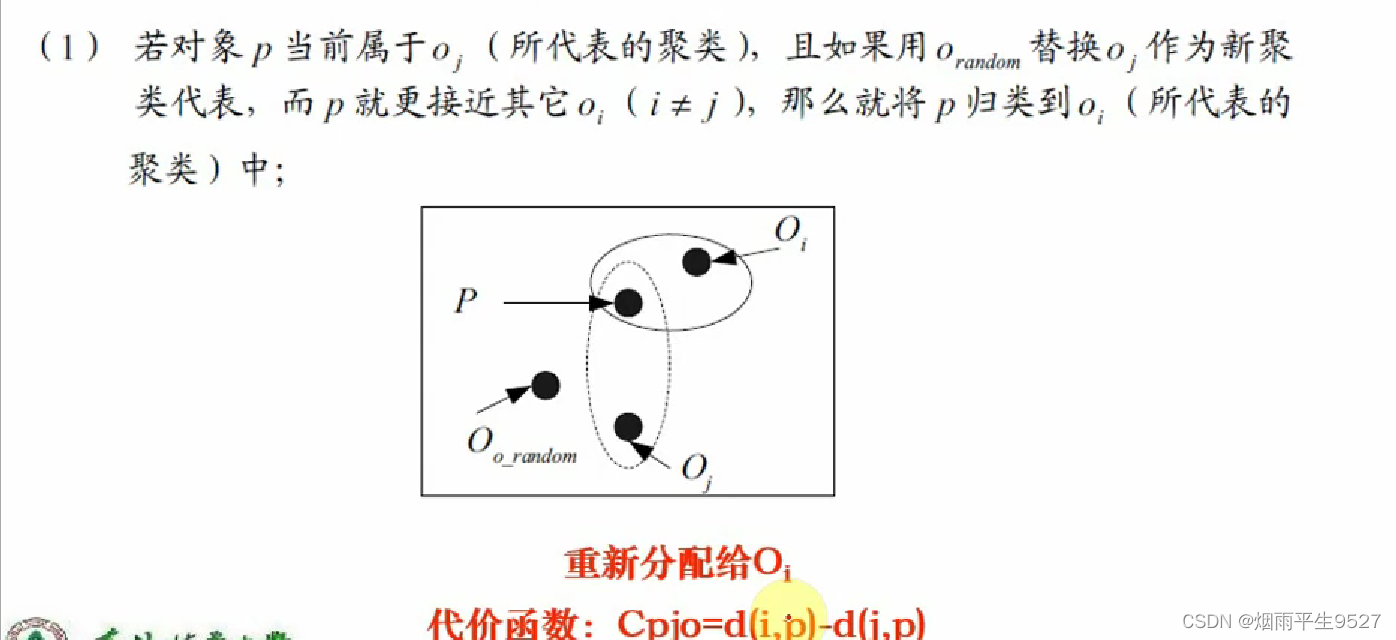
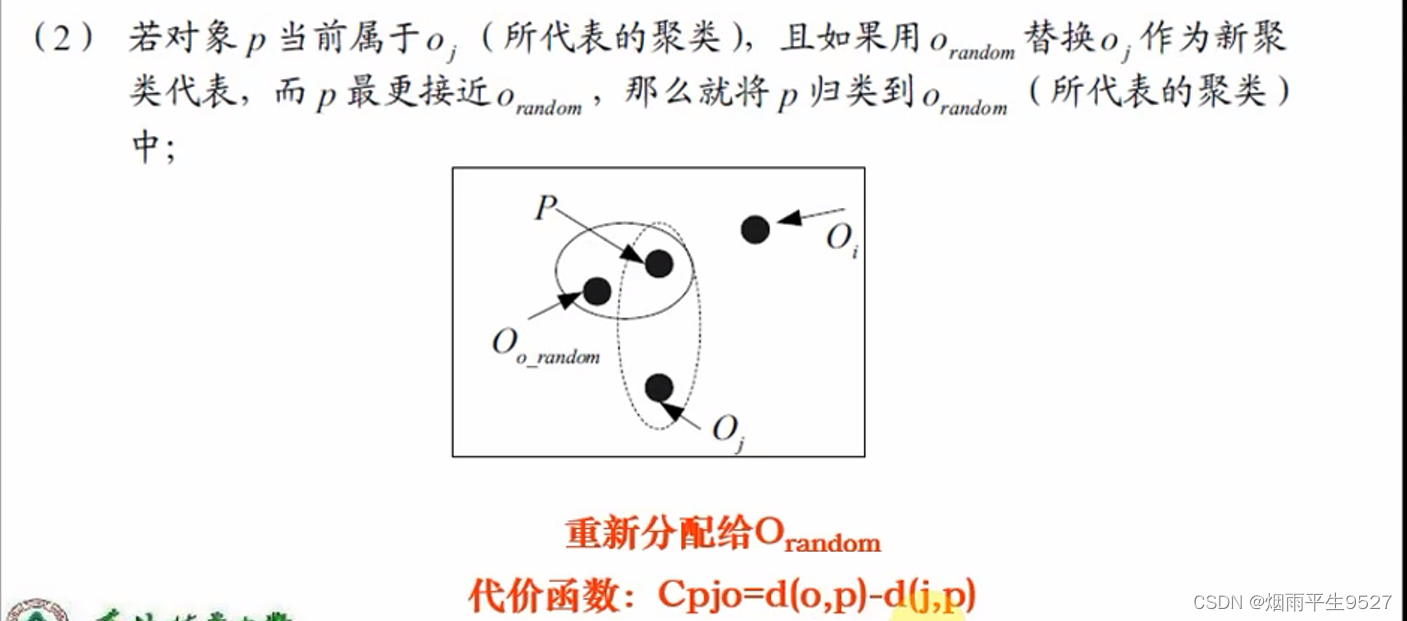
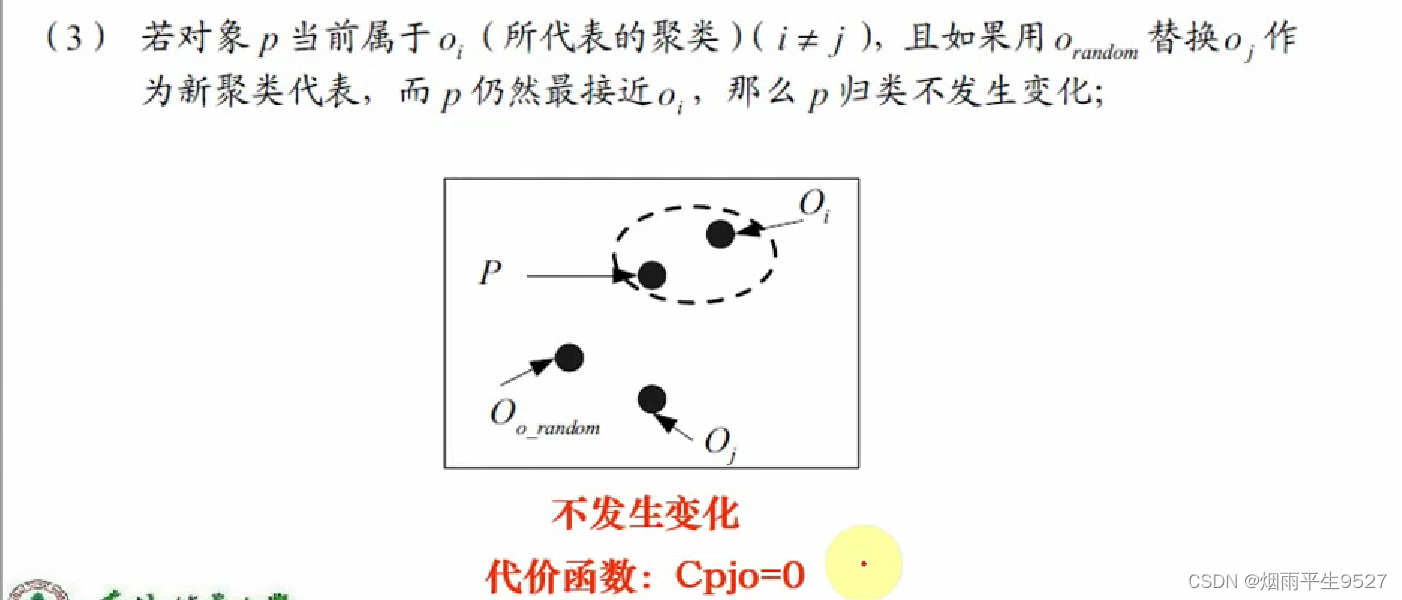
4.算法步骤
- 选取聚类中心:随机从n个数据对象选择k个
- 循环3-5,知道聚类不发生变化
- 对剩余的每个对象,根据各个聚类中心的距离,将其划分给最近的聚类。
- 选择任意非中心对象
计算与中心对象
交换的成本S。
- 若成本S为负,则交换中心对象。
五、基于层次的聚类方法
5.1 总述
- 给定的数据对象集合进行层次分解,根据层次分解的方式,层次的方法被分为凝聚、分裂。
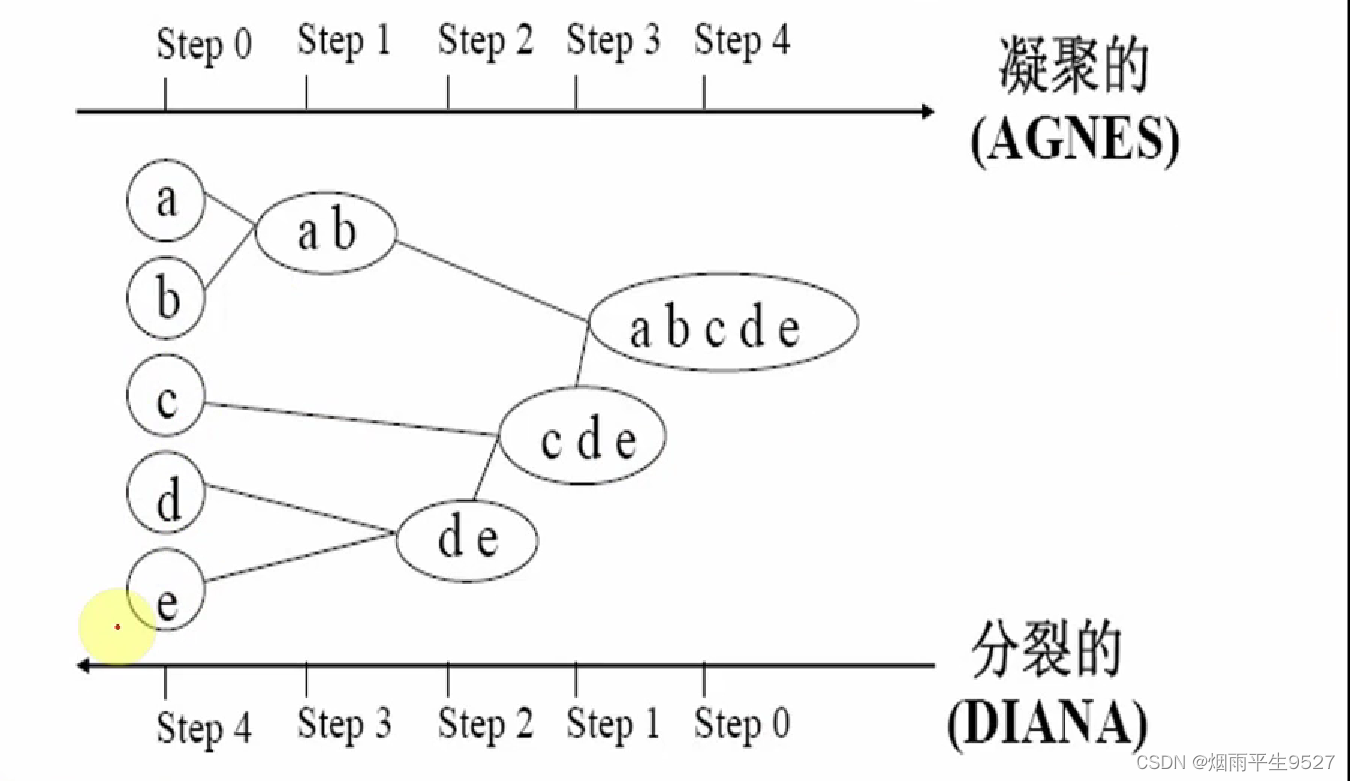
- 凝聚层次法(agnes算法)
- 自底向上
- 一开始将每个对象作为单独的一组,然后合并相近的组,直到合为一组或到达终止条件
- 分裂层次法(dinan算法)
- 自底向下
- 所有对象置于一个簇,在迭代的每一步,一个簇被分裂为更下的簇,直到每个对象单独为一个簇或到达某个终止条件
- 计算距离方法

5.2agnes算法
- 步骤:
- 每个对象当做一个初始簇
- repeant 3-4
- 根据两个簇中最近数据点找到最近的两个簇
- 合并两个簇,生成新的簇集合
- until 达到定义的簇的数目
- 例子

- 特点:
- 算法简单,合并会出现问题:一旦合并就不能撤销,可能会对后续操作产生影响。
- 复杂度比较大O(n^2)
5.3diana算法
- 簇的直径:一个簇中的任意两个数据点的距离中的最大值
- 平均相异度(平均距离):

- 算法步骤
将所有对象当做一个初始簇 for(int i = 1; i <= k; i++){ 在所以簇中挑选出最大直径的簇C 找出C中与其他点平近距离最大的一个点p放入splinter group,剩余点放入old party Repeat 在old party中找出到splinter group比到old party更近的点,加入splinter group Until 没有新的点被分到splinter group splinter group 与 old party 就被分解为两个新的簇 } -
例题

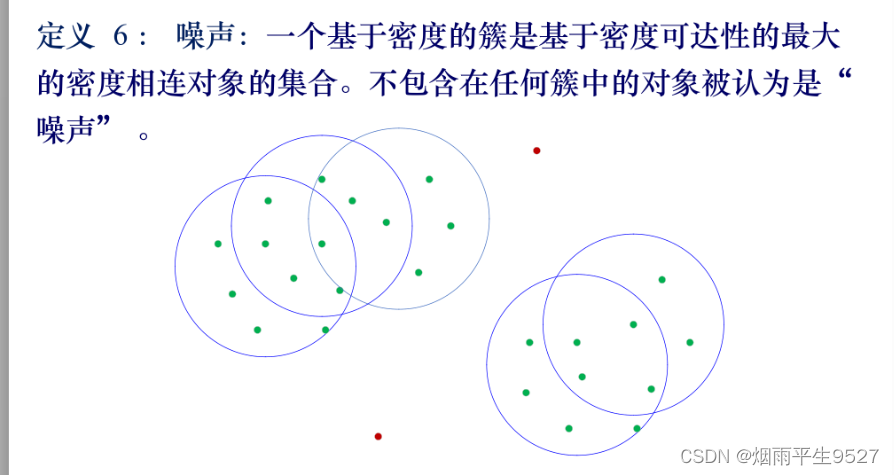
六、 基于密度的聚类方法
6.1概述
- 基于密度聚类方法
- 只要一个区域中点的密度(对象、数据点的数目)超过阈值,就将其加到与之相近的聚类中
- 可以过滤噪声、孤立点、发现任意形状的簇
- 代表算法:Dbscan、Optics、Denclue