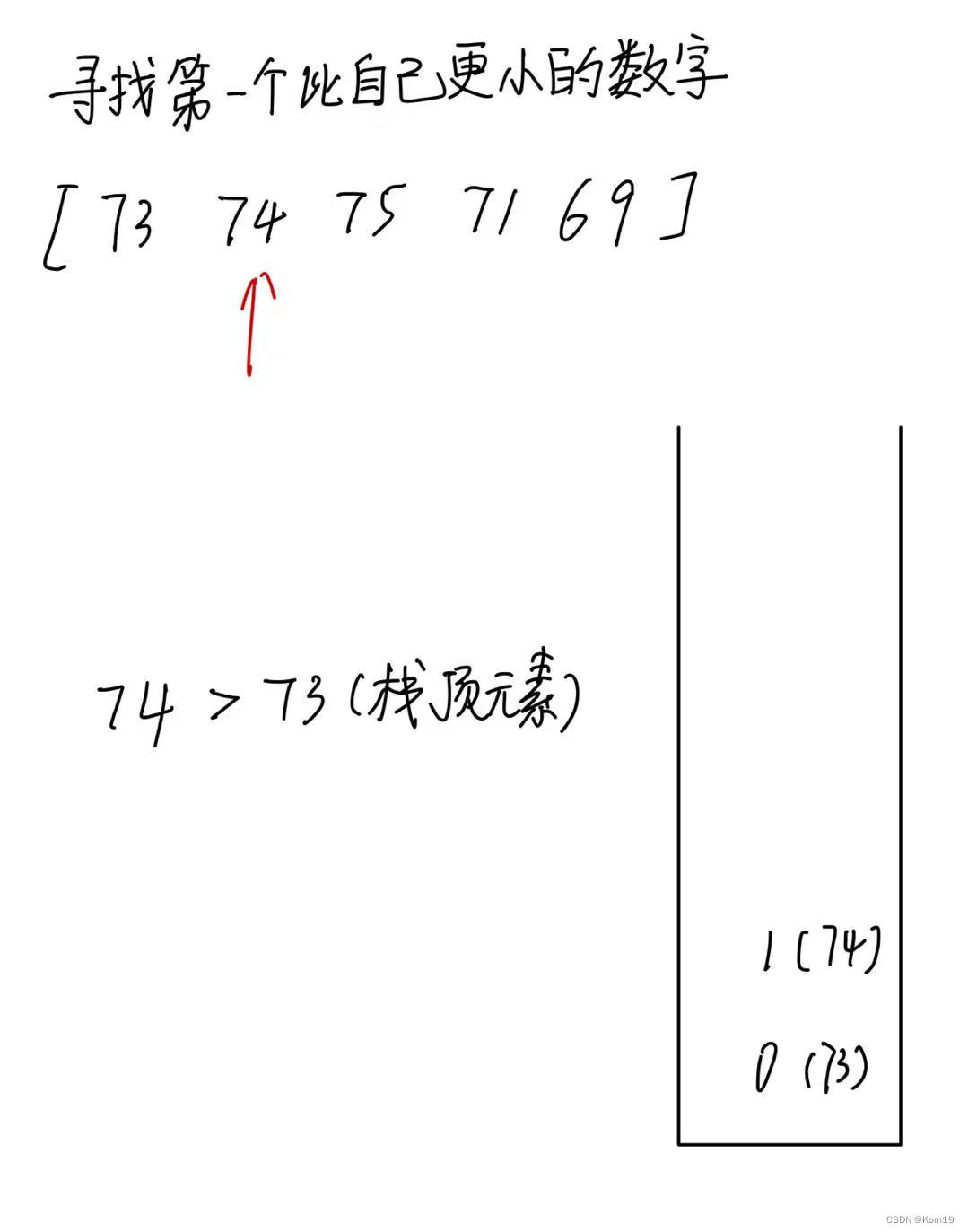
首先我们要搞懂什么时候使用单调栈?
当我们需要找到 左边或右边 第一个 比自己大的数 或者 比自己小的数 时就要使用单调栈
单调栈实际上就是一个栈,他的作用就是存储我们遍历过的数字。当我们遍历数组的时候,遍历到后面的数组后并不知道前面遍历过的元素是什么,所以单调栈的作用就是用于存储遍历过的数字。
使用单调栈需要注意的事项
1.确定栈内的元素的单调顺序(重要) 2.确定单调栈内存放的元素
介绍完单调栈的本质以及使用的注意事项以后就来介绍一下怎么用单调栈寻找左边或右边第一个 比自己大的数或者比自己小的数了
注意我们数组里面存放的是数组下标,便于我们第一个更大或更小的元素距离自身有多远

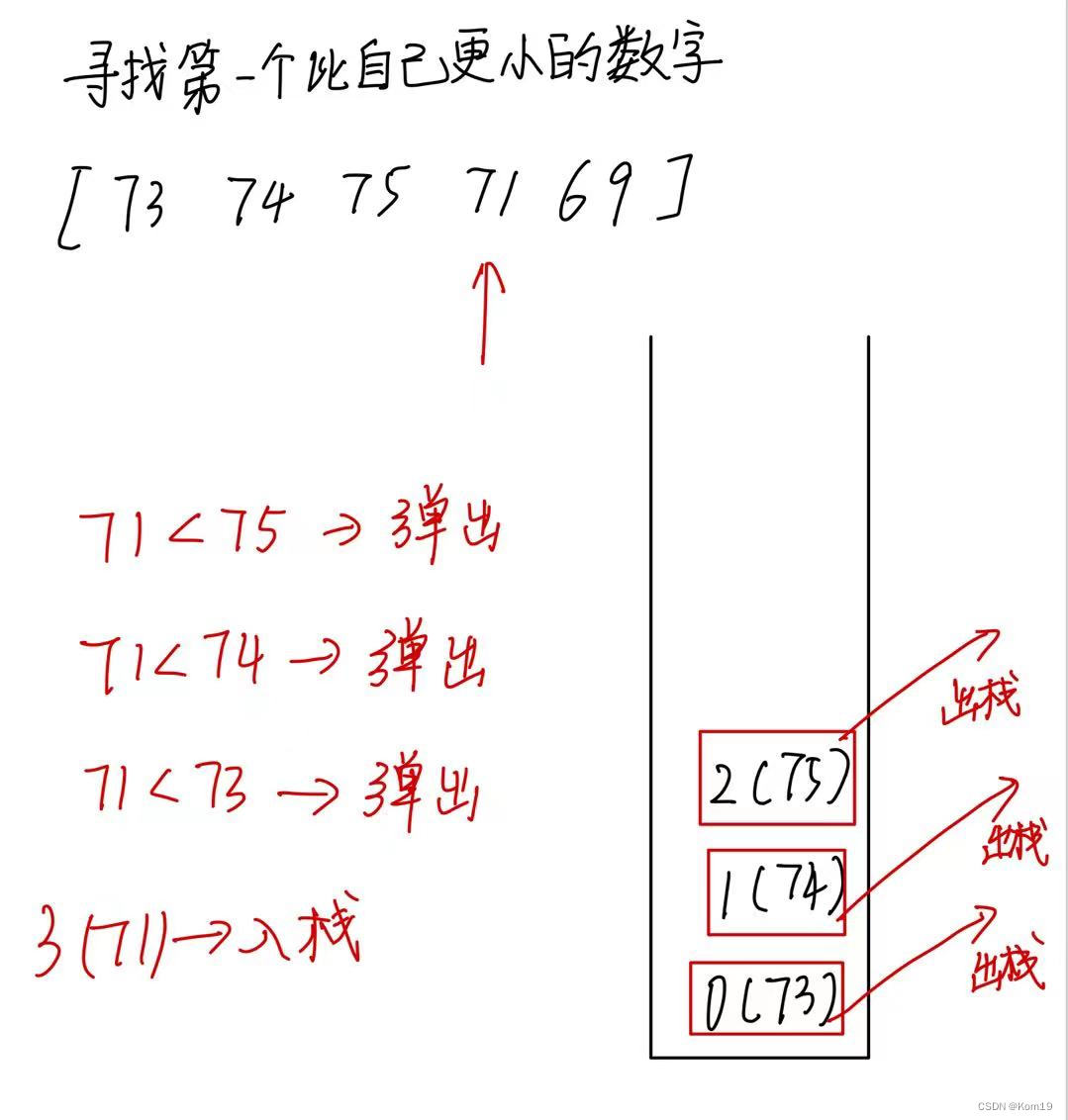
了解完怎么使用单调栈以后就来看看常见的单调栈题目了
739. 每日温度
题意:给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后
那么也就是寻找下一个更小的元素那么我们就使用单调栈
首先明确两点:1.栈内元素是单调递增 (从栈底到栈顶)2.栈内存放的是数组的下标
那么当栈顶元素大于数组元素时
那么直接入栈
if(num <= temperatures[stack.peek()]){
stack.push(i);
}当栈栈顶元素小于数组元素时
那么不断比较栈顶元素,直到栈顶元素小于该遍历元素
while(!stack.isEmpty() && num > temperatures[stack.peek()]){
int top = stack.peek();
result[top] = i - top;
stack.pop();
}
stack.push(i);最后要我们返回的是该日究竟在几天后才会出现温度更低的情况,所以我们的返回数组里面存放的是距离
所以才会有这段代码
result[top] = i - top;最后贴上完整代码
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int len = temperatures.length;
int[] result = new int[len];
//创建单调栈
Stack<Integer> stack = new Stack();
stack.push(0);
//遍历温度
for(int i = 1;i < len;i++){
int num = temperatures[i];
if(num <= temperatures[stack.peek()]){
stack.push(i);
}else{
while(!stack.isEmpty() && num > temperatures[stack.peek()]){
int top = stack.peek();
result[top] = i - top;
stack.pop();
}
stack.push(i);
}
}
return result;
}
}496. 下一个更大元素 I
寻找更大的元素问题,那么我们还是使用单调栈来解决
这道题有两个数组,一个nums1 一个nums2,题目是想要在 nums2 中找到 nums1 中每个值的下一个更大元素,我这里使用哈希表来建立映射关系,将nums1中的元素和下标都放进哈希表里面
还是在nums2中使用单调栈存遍历过的元素,当发现更大的元素以后就弹出栈顶元素,但是这里跟以往不同的地方在于,我们需要检查栈顶元素是否存在于哈希表中,如果存在那么就在相应的下标处(新建好的数组)存放更大的元素
if(map.containsKey(nums2[stack.peek()])){
int index = map.get(nums2[stack.peek()]);
result[index] = nums2[i];
}总体的思路解决完了,现在就来直接写代码
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int len = nums1.length;
//创建result数组
int[] result = new int[len];
Arrays.fill(result,-1);
//创建映射关系
HashMap<Integer,Integer> map = new HashMap();
for(int i = 0;i < nums1.length;i++){
map.put(nums1[i],i);
}
//创建单调栈
Stack<Integer> stack = new Stack();
stack.push(0);
//遍历数组
for(int i = 1;i < nums2.length;i++){
if(nums2[stack.peek()] >= nums2[i]){
stack.push(i);
}else{
while(!stack.isEmpty() && nums2[stack.peek()] < nums2[i]){
if(map.containsKey(nums2[stack.peek()])){
int index = map.get(nums2[stack.peek()]);
result[index] = nums2[i];
}
stack.pop();
}
stack.push(i);
}
}
return result;
}
}503. 下一个更大元素 II
还是每日温度的变式,现在我们是按照数组循环来找到更大的元素
面对数组循环问题,我们通常使用将 遍历长度为数组的两倍 来进行解决
然后 数组下标 = 数组下标%数组长度 的方式来解决
这里画了一幅图来解释
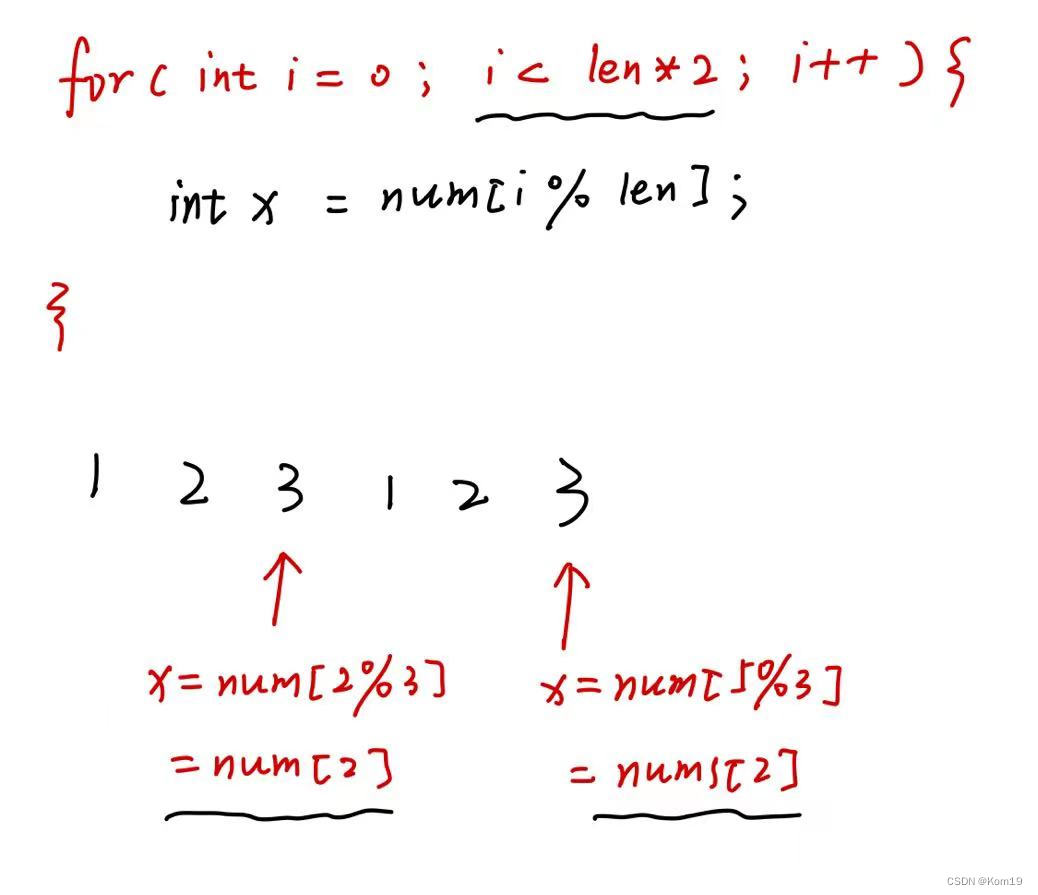
关键的难点解决了剩下就简单了 直接上代码
class Solution {
public int[] nextGreaterElements(int[] nums) {
int len = nums.length;
//创建结果数组
int[] result = new int[len];
Arrays.fill(result,-1);
//创建单调栈
Stack<Integer> stack = new Stack();
stack.push(0);
//遍历数组
for(int i = 1;i < 2*len;i++){
if(nums[i % len] <= nums[stack.peek()]){
stack.push(i % len);
}else{
while(!stack.isEmpty() && nums[i % len] > nums[stack.peek()]){
result[stack.peek()] = nums[i % len];
stack.pop();
}
stack.push(i % len);
}
}
return result;
}
}42. 接雨水
接雨水是最经典的一道面试题了,接下来就来看看怎么解决
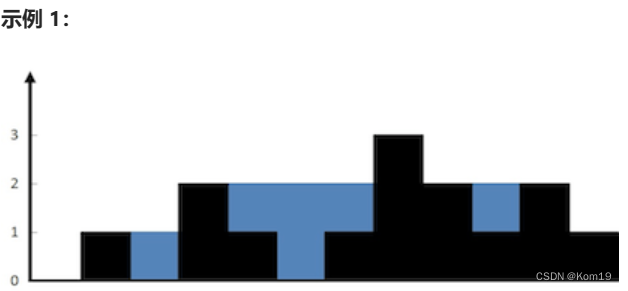
以示例1为例子,我们看到从左向右,当遇到比自己更高的柱子就可以接住雨水
那么很明显我们可以转换成单调栈问题,即寻找更大的元素
假如说我们找到了更高的柱子,那么又应该怎么来处理雨水的面积呢?
计算面积是需要3个点的,左中右才能计算出雨水的面积,不理解的同学可以参考下面这张图
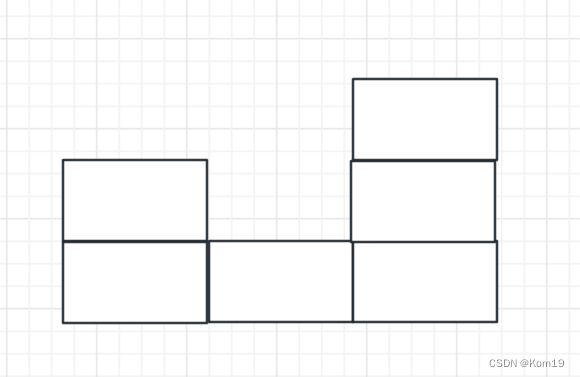
右边的柱子是遇到的更大高度,中间的柱子是弹出的栈顶元素,左边的柱子是没有弹出的栈顶元素
我们将 右边柱子的下标 - 左边柱子的下标 - 1 作为雨水的宽度
将 左右两个柱子的更低高度 - 中间柱子的高度 作为雨水的高度
(为什么是最低还是可以参考上面这张图)
那么雨水的面积就等于 雨水的高度 x 雨水的宽度
同时也要牢记 雨水的面积是一步一步累加加起来的
分析完怎么计算雨水面积以后我们就来分析一下这一块的面积
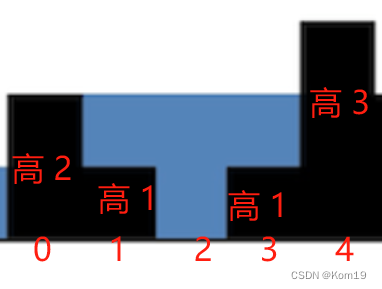
一步一步分析
第一步
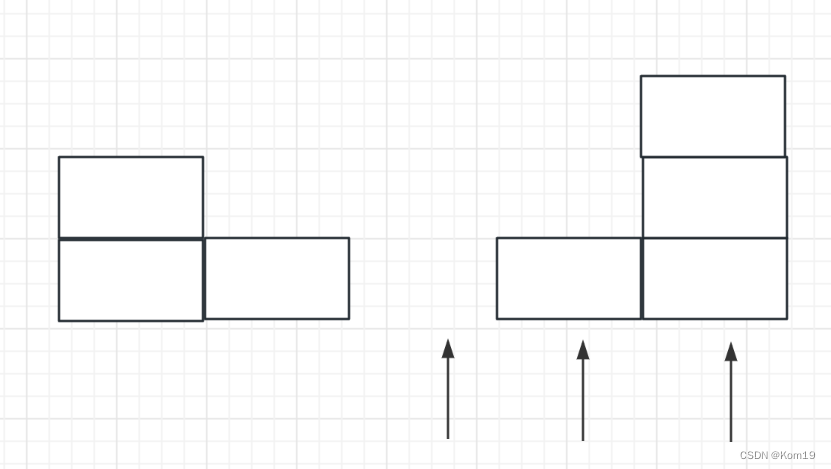
这一块面积根据计算我们可以得出接到的雨水面积是 -1
第二步
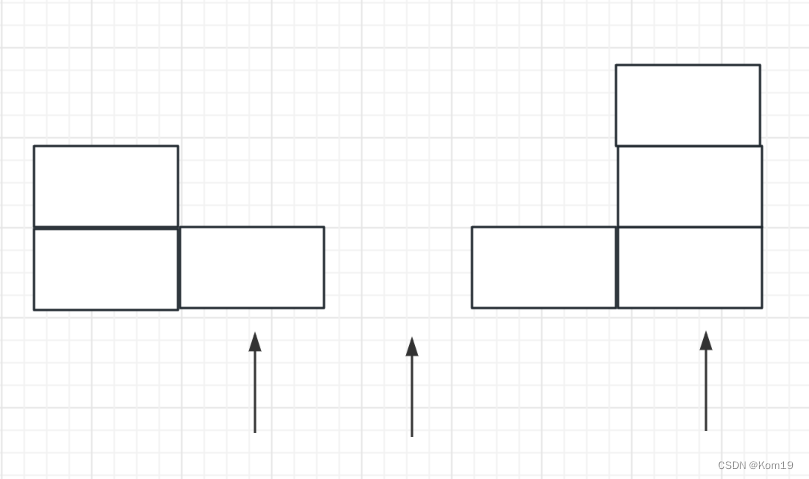
这一块面积根据计算我们可以得出接到的雨水面积是 2
第三步
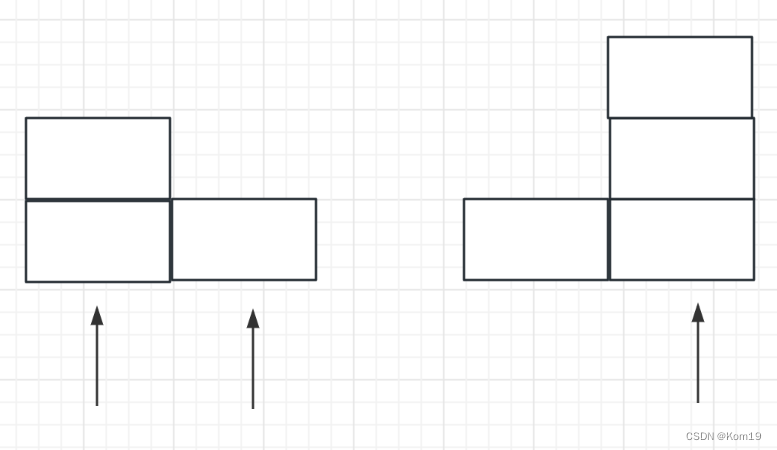
这一块面积根据计算我们可以得出接到的雨水面积是 3
那么累加起来我们就可以得到这一块的面积是4了
具体分析完我们直接上代码
public int trap(int[] height) {
int len = height.length;
int ans = 0;
//创建单调栈
Stack<Integer> stack = new Stack();
stack.push(0);
//遍历数组
for(int i = 1;i < height.length;i++){
if(height[i] <= height[stack.peek()]){
stack.push(i);
}else{
while(!stack.isEmpty() && height[i] > height[stack.peek()]){
//需要三个元素
int mid = stack.pop();
if(!stack.isEmpty()){
int left = stack.peek();
int w = i - left - 1;
//计算高度
int h = Math.min(height[left],height[i]) - height[mid];
int s = h*w;
ans += s;
}
}
stack.push(i);
}
}
return ans;
}84. 柱状图中最大的矩形
同样是寻找最大的面积,但是本题的做法与上一题相反,上一题是寻找更大的元素
但是本题的做法则是寻找更小的元素
为什么?我们可以举例说明
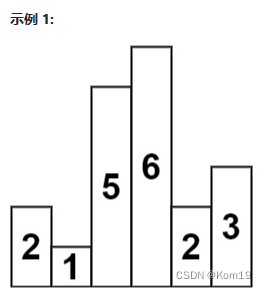
想要获得最大的面积 我们就需要得到最高柱子两边的高度 这与接雨水的解题思路是相反的
接雨水是想要获得最大面积,需要获得最低柱子两边的的高度
那么 获得最高柱子右边的高度,那么就要用到 单调栈 来寻找了(很显然是寻找更小的元素)
虽然解题思想不一样,但是本题的很多细节还是和接雨水相同的
比如处理面积,那么还是一样的做法,计算出宽度的方式还是 right - left - 1通过左右边柱子计算出宽度
但是高度的处理方式就不一样了,这里是直接用栈顶弹出柱子的高度
那么分析完毕 我们直接上代码
class Solution {
public int largestRectangleArea(int[] heights) {
int ans = 0;
//创建单调栈 单调递减
Stack<Integer> stack = new Stack();
stack.push(0);
//创建新数组
int len = heights.length;
int[] newHeight = new int[len + 2];
newHeight[0] = 0;
newHeight[len + 1] = 0;
for(int i = 1;i < len + 1;i++){
newHeight[i] = heights[i-1];
}
//遍历数组
for(int i = 1;i < newHeight.length;i++){
//保证单调递减
if(newHeight[i] >= newHeight[stack.peek()]){
stack.push(i);
}else{
while(!stack.isEmpty() && newHeight[i] < newHeight[stack.peek()]){
int mid = stack.pop();
if(!stack.isEmpty()){
int left = stack.peek();
int right = i;
//计算宽度
int w = right - left - 1;
//计算高度
int h = newHeight[mid];
//计算面积
ans = Math.max(h*w,ans);
}
}
stack.push(i);
}
}
return ans;
}
}这里大家可能会有疑惑的地方在于,为什么要创建一个新的数组,同时将数组头部和尾部的值设置成0呢
这是为了防止数组也是单调递减或者单调递增的的,假如说我们遇到了这样的数组

那么一直找不到更小的元素,我们的单调栈岂不是没有用了?
如果遇到这样的数组

以第一个柱子为基准,由于没有左边的柱子,那么又该怎么样来计算呢?
所以为了防止这样的情况发生,我们直接创建的一个新的数组,将数组头和尾设置成0方便计算
单调栈的题目其实并不难,直接记住了模板(参考每日温度)那么就是细节的处理了