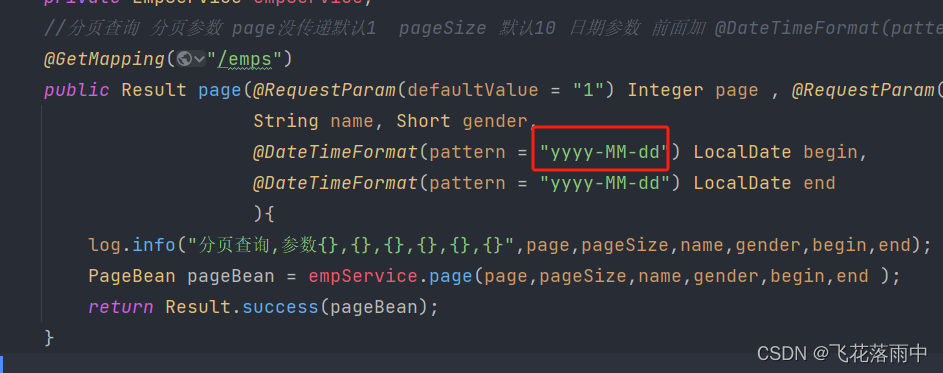
卡尔曼滤波器
什么是卡尔曼滤波器?
鉴于测量结果会受到噪声的影响,卡尔曼滤波器 (KF) 算法可以恢复被跟踪的底层对象的真实状态。该算法有两个步骤:预测步骤和测量更新步骤。该滤波器结合了噪声传感器的测量结果和基于物理的模型的预测(例如,速度*时间给出距离)以提供最佳估计。让我们尝试使用 GPS 传感器来估计汽车的位置。众所周知,GPS 传感器无法准确预测车辆的位置(这对于自动驾驶汽车等安全关键型应用至关重要),我们的目标是预测车辆的实际位置。

汽车在前一个时间步的位置,k-1
上图使用高斯分布显示了前一个时间步的汽车位置。方差表示估计的准确程度。在这种情况下,方差越小,准确度越高。
在滤波器的预测阶段,它使用物理模型预测当前时间步 k 的汽车位置。下图展示了汽车在另一个方差较大的高斯分布中的新位置。这是因为新位置是使用简单的物理模型计算的,没有来自传感器的任何数据。这意味着汽车的位置可以位于该分布中的任何位置。

汽车在之前时间步的位置和预测
在测量更新阶段,我们从GPS传感器获取汽车的当前位置,如下图橙色分布所示。

汽车在预测和测量更新步骤中的位置
由于 GPS 传感器也存在噪声,因此我们将预测结果与传感器测量结果结合起来来估计最佳位置,如下所示。这是通过将这两个概率函数相乘来完成的,结果也将是另一个高斯函数。

组合两个位置给出了汽车在时间 x_k 时的位置的最佳状态估计
这样,即使传感器的测量结果有噪声,我们也可以估计被跟踪物体的真实状态。

卡尔曼滤波器中的 Twp 步长,其中 x 是平均值,p 是方差。
上图显示了卡尔曼滤波器中估计被跟踪对象的真实状态的步骤。在更新步骤中,我们使用预测步骤的预测值和测量值来查找估计中的误差。卡尔曼增益可以控制应该给预测值和测量值赋予多少权重。该参数决定真实状态是否更接近预测值或测量值。
K = 预测误差 /(预测误差 + 测量误差)[4]
使用这些值,我们可以在更新步骤中找到真实状态(x_k 和 P_k)。请注意,我们还使用其他参数来应用 KF,为了简单起见,这里没有公开。
股票交易中的KF

蓝线移动平均线的计算,窗口大小为 50 天,
该算法在股票交易中的用例之一是我们可以使用它来平滑类似于移动平均线(MA)的定价数据。
移动平均线是一种技术分析工具,通过创建不断更新的平均价格来帮助平滑价格数据。交易者通常使用它来识别趋势和潜在的交易机会。
KF 相对于 MA 的优点之一是它不需要窗口长度,从而减少了过度拟合的问题。
Python 中的实现
我已经实现了股票交易中算法用例的示例代码,并将其发布在GitHub 存储库中。如果你想玩的话请看一下。以下是实现该算法的步骤。
- 导入数据
-
# Load pricing data for a security df = pd.read_csv('data/IFNNY.csv') x = df['Adj Close']
2.主要可以利用pykalman来实现算法。该算法需要初始化默认参数来估计真实状态。我们为这些参数采用了常用的默认值。
# Construct a Kalman filter
kf = KalmanFilter(transition_matrices = [1],
observation_matrices = [1],
initial_state_mean = 0,
initial_state_covariance = 1,
observation_covariance=1,
transition_covariance=.0001)3. 计算滚动平均值和协方差。
mean, cov = kf.filter(x.values)
mean = pd.Series(mean.flatten(), index=x.index)4. 为了进行比较,我们可以计算 30 天和 60 天窗口的移动平均线。
# Compute the rolling mean with various lookback windows
mean30 = x.rolling(window = 30).mean()
mean60 = x.rolling(window = 60).mean()5. 我们可以绘制使用卡尔曼滤波器计算出的 30 天和 60 天移动平均值的滚动平均值。

正如您所看到的,与移动平均线相比,卡尔曼的估计更加平滑并且不会过度拟合。