1. 梯度（Gradient）的理解

深度学习尝试在权重空间中找到一个方向，沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向，因为可以直接计算出最好的方向，这就是从数学上计算出最陡峭的方向。这个方向就是损失函数的梯度（gradient）。在蒙眼徒步者的比喻中，这个方法就好比是感受我们脚下山体的倾斜程度，然后向着最陡峭的下降方向下山。

梯度的定义
在函数各个点的变化率的一个向量, 向量的模就是方向导数的值
性质：梯度是个有大小的值的向量；最大方向导数的值（向量的模）就是梯度方向；梯度的值就是最大方向导数的值。
通俗理解梯度：给一个函数/标量场，出一个矢量场(方向为每点方向导数值最大的方向，大小为其变化率的矢量组成的矢量场)。
简单来说：梯度不是一个值，而是一个方向

2. 导数

导数精确描述了函数变化率，变化率可理解为变量的变化“快慢”问题。
研究变化率的问题前首先引入一个一元函数 y=kx+b，函数就一个未知数x，x也叫自变量。针对这个一元函数中的某个特定点x0，该点的导数就是x0点的“瞬间斜率”，也即切线斜率。对一维函数的求导公式如下：

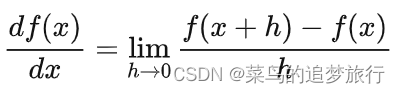
在一维函数中，斜率是函数在某一点的瞬时变化率。如果这个斜率越大，就表明其上升趋势越强劲。当这个斜率为0时，就达到了这个函数的“强弩之末”，即达到了极值点。

梯度是函数的斜率的一般化表达，它不是一个值，而是一个向量。在输入空间中，梯度是各个维度的斜率组成的向量（或者称为导数derivatives）。在单变量的一元函数中，梯度可简单理解为只是导数，或者说对于一个线性函数而言，梯度就是曲线在某点的斜率。

3. 偏导数

研究多元函数的时候就出现了偏导。偏可以理解成部分，多元就是一个自变量固定，在编程里叫常量。当函数有多个参数的时候，我们称导数为偏导数。而梯度就是在每个维度上偏导数所形成的向量。

偏导数是多元函数“退化”成一元函数时的导数，这里“退化”的意思是固定其他变量的值，只保留一个变量，依次保留每个变量，则𝑁元函数有𝑁个偏导数。
一个变量对应一个坐标轴，偏导数为函数在每个位置处沿着自变量坐标轴方向上的导数（切线斜率）。

式$z=f(x,y)$ 的偏导数
函数在点 $（x0,y0）$ 沿着 $x$ 轴方向的变化率

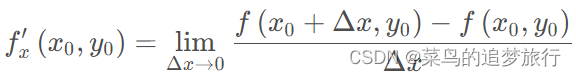
$z=f(x,y)$ 的偏导数
函数在点 $（x0,y0）$ 沿着 $y$ 轴方向的变化率

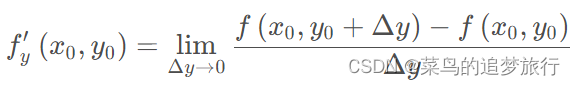
4. 方向导数

方向导数的本质是一个数值，简单来说其定义为：一个函数沿指定方向的变化率。

构建方向导数需要有两个元素：

1. 函数
2. 指定方向

当然，与普通函数的导数类似，方向导数也不是百分之百存在的，需要函数满足在某点处可微，才能计算出该函数在该点的方向导数。
我们将下图看作是一座山的模型，我们处在山上的某一点处，需要走到山下。理论上来说，这座山的表面是可以通过一个函数的描述的（虽然想要找到这个函数可能很难），而这个函数可以在不同的方向上都确定出一个方向导数，这就好比于如果我们想下山，道路并不是唯一的，而是可以沿任何方向移动。区别在于有些方向可以让我们下山速度更快，有些方向让我们下山速度更慢，有些方向甚至引导我们往山顶走（也可以理解为下山速度时负的）。在这里，速度的值就是方向导数的直观理解。

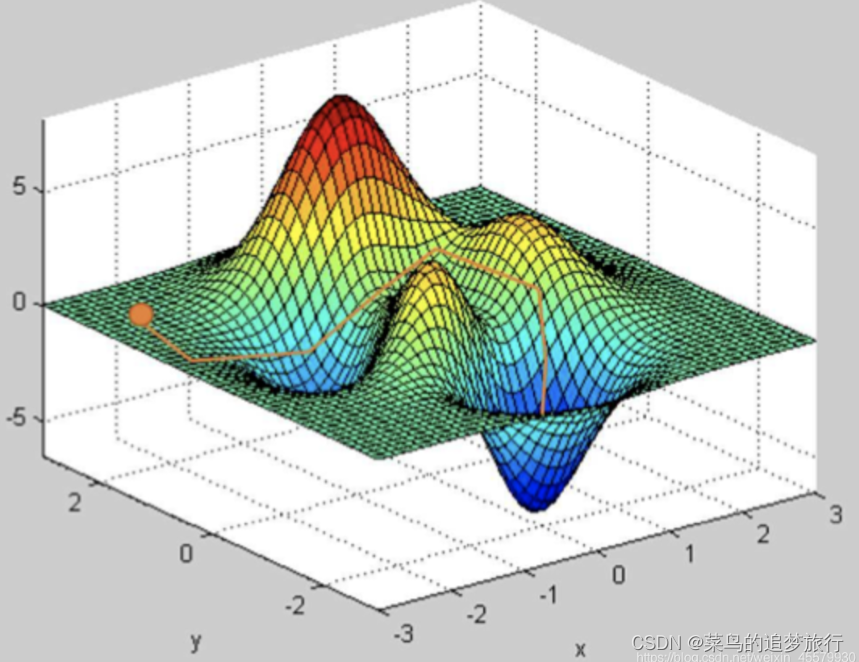
5.总结

方向导数是各个方向上的导数

偏导数连续才有梯度存在

梯度：函数在某点的梯度是这样一个向量，它的方向是函数在这点方向导数取得最大值得方向，它的模（即梯度的值）为方向导数的最大值.
解释什么是向量的模？
向量的模就是向量的长度
假设平面有两个点 $A(x1,y1)$，$B(x2,y2)$
)，它们之间的距离是(还是勾股定理)

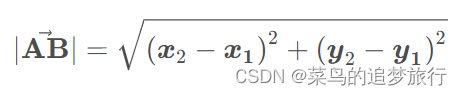
这类距离也叫欧式距离，在机器学习中叫2-范数

梯度的符号$\mathrm{grad}f(x_0,y_0)$或者 $\nabla f(x0,y0)$， 梯度的表达式如下所示：

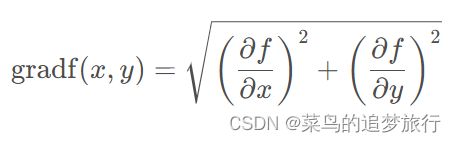
参考博客链接：
https://blog.csdn.net/qq_37553011/article/details/79795092
https://blog.csdn.net/flyfish1986/article/details/88562514
https://blog.csdn.net/weixin_45579930/article/details/112185689
向博主致谢！