560. 和为 K 的子数组

560. 和为 K 的子数组

题目描述：

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

子数组是数组中元素的连续非空序列。

 

解题思路：

我们可以很容易想到暴力解法，但是时间复杂度为N^2，我们可以是用前缀和对其优化

 我们可以利用前缀和数组sum来记录，sum【i】代表到i位置的子数组之和

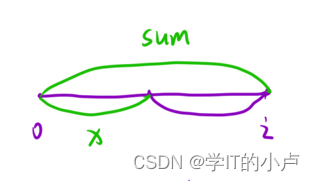
假设这是0-i的数组后面的我们先不看，我们可以将其分成两部分，一部分之和为k，另外一部分为sum【i】-k，本题是求和为k的数组的个数

那问题就可以变为在sum【i】-k中有多少个子数组等于sum【i】-k

这段区间正负都有，子区间可能不只有一个噢！！！

我们可以利用hash来完成本题，一个参数为前缀和，一个参数为次数 ，都是int类型

我们可以利用一个int变量来代替sum数组，因为sum不用每个都记录下来，只要记录上一个位置

解题代码：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int,int>hash;
        hash[0]=1;
        int ret=0;
        int sum=0;
        for(auto x:nums)
        {
            sum+=x;
            if(hash.count(sum-k))ret+=hash[sum-k];
            hash[sum]++;
        }
        return ret;
    }
};

---

 974. 和可被 K 整除的子数组

974. 和可被 K 整除的子数组

题目描述：

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目。

子数组 是数组的 连续 部分。

解题思路：

解决本题我们先来补充两个知识点 

• 同余定理：（a-b）/p=k....0可以转换为a%p=b%p，具体证明可见同余定理_百度百科 (baidu.com)
•  C++中，负数（a）%正数（p），在C++负数求余正数正确应该为正数，但是计算结果为负数，我们对其修正时期变成a%p+p，但是为了考虑到正负统一的问题，我们再次进行修正让其变为（a%p+p）%p

接下来我们来看一下本题，本题如果你做了上一题，你会发现基本上是类似的

只不过判断条件不太一样罢了

题目要求的可以被k整除的数组为图中sum-x部分，那就变成（sum-x）%k==0也就变成了sum%k==x%k，也就转为为在【0，i-1】这个区间内有多少个前缀和的余数等于sum%k

解题代码： 

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int>hash;
        hash[0%k]=1;
        int ret=0;
        int sum=0;
        for(auto x:nums)
        {
            sum+=x;
            int r=(sum%k+k)%k;
            if(hash.count(r))ret+=hash[r];
            hash[r]++;
        }
        return ret;
    }
};