K近邻算法
- 1. K近邻算法简介
- 2. K近邻算法常见距离度量
- 2.1 欧氏距离(Euclidean Distance)
- 2.2 曼哈顿距离(Manhattan Distance )
- 2.3 切比雪夫距离(Chebyshev Distance)
- 2.4 闵可夫斯基距离(Minkowski Distance)
- 2.5 标准化的欧几里得距离(Standardized Euclidean Distance)
- 2.6 余弦距离(Cosine Distance)
- 3. K值的选择
- 4. KD树(K-Dimensional Tree)
- 5. 最近领域搜索(Nearest Neighbor Lookup)
- 6. KD树的应用
1. K近邻算法简介
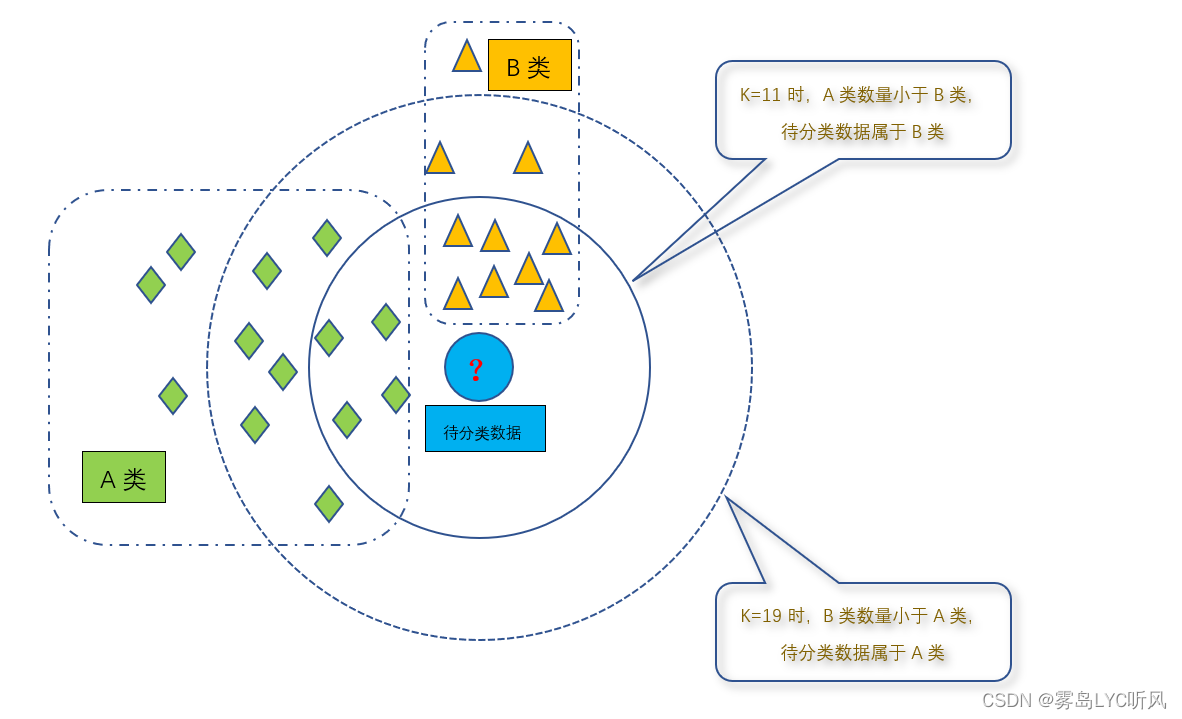
| K近邻算法:K近邻(K-Nearest Neighbors,简称KNN)算法是一种监督学习算法,用于分类和回归问题 基本原理:对于给定的未标记样本,通过计算其与已标记样本之间的距离,然后选取距离最近的K个样本作为其邻居 分类问题:通过统计这K个邻居中各类别的数量,将未标记样本归为数量最多的类别 回归问题:以基于这K个邻居的属性值进行加权平均或其他方式预测目标变量的值 K近邻算法的三个基本要素 Ⓐ 距离度量方法 Ⓑ K值的选择 Ⓒ 分类决策规则 |
K近邻算法的分类问题
2. K近邻算法常见距离度量
| 距离公式:距离公式是用来衡量两个点之间的距离的数学表达式 基本性质:通过统计这K个邻居中各类别的数量,将未标记样本归为数量最多的类别 非负性:任意两个点之间的距离始终非负,即距离不会小于零 同一性:对于两个点A和B之间的距离,如果A和B的顺序颠倒,距离的值不变,即d(A, B) = d(B, A) 齐次性:对于两个点A和B之间的距离,如果将其中一个点固定,并将另一个点与其位置相对应地进行缩放或伸展,距离也会相应地按比例缩放或伸展 三角不等式:对于三个点A、B、C之间的距离,有d(A, C) ≤ d(A, B) + d(B, C)。即通过两个点的任意中间点的路径总长不会超过直接连接这两个点的路径长度 |
► 在机器学习中,函数 d i s t ( x i , x j ) {dist(x_i,x_j)} dist(xi,xj)表示点 i {i} i 和点 j {j} j 之间的距离需要满足:
⮚ 非负性: d i s t ( x i , x j ) ≥ 0 {dist(x_i,x_j)≥0} dist(xi,xj)≥0;
⮚ 同一性: d i s t ( x i , x j ) = 0 , 当且仅当 X i = X j {dist(x_i,x_j)=0},当且仅当{X_i=X_j} dist(xi,xj)=0,当且仅当Xi=Xj;
⮚ 对称性: d i s t ( x i , x j ) = d i s t ( x j , x i ) {dist(x_i,x_j)=dist(x_j,x_i)} dist(xi,xj)=dist(xj,xi);
⮚ 直递性: d i s t ( x i , x j ) ≤ d i s t ( x i , x k ) + d i s t ( x k , x j ) {dist(x_i,x_j)≤dist(x_i,x_k)+dist(x_k,x_j)} dist(xi,xj)≤dist(xi,xk)+dist(xk,xj);
2.1 欧氏距离(Euclidean Distance)
| 欧式距离:也称欧几里得距离,是最常见的距离度量,衡量的是多维空间中两个点之间的绝对距离 优点 直观简单:欧氏距离是最为简单和直观的距离度量之一(通过计算两个点在各个坐标轴上的差值的平方和再开方得到距离值) 广泛适用:欧氏距离适用于大多数连续型数据的度量(几何空间中的点、向量) 特征独立:欧氏距离在计算时对于各个维度的特征是独立的,即不同维度之间的距离互不影响 不足 Ⓐ 敏感性:欧氏距离对异常值和噪声敏感(异常值或噪声,可能会导致欧氏距离计算的结果失真) Ⓑ 缺乏标准化:欧氏距离对各个维度的尺度敏感(当输入数据的不同维度具有不同的尺度时,欧氏距离计算结果可能会被主导由尺度较大的维度,影响特征之间的相似性度量) Ⓒ 高维问题:在高维空间中,欧氏距离的计算可能会受到所谓的“维度灾难”问题的影响 Ⓓ 数据假设:欧氏距离假设数据分布是均匀的,并且各个维度之间是相互独立的(在某些实际应用中,这些假设可能不成立,欧氏距离的应用效果会受到限制) |
- 数学公式
二维平面的点 a ( x 1 , y 1 ) {a(x_1,y_1)} a(x1,y1) 与点 b ( x 2 , y 2 ) {b(x_2,y_2)} b(x2,y2) 间的欧式距离
d ( a , b ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 {d_{(a,b)}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}} d(a,b)=(x1−x2)2+(y1−y2)2
三维平面的点 a ( x 1 , y 1 , z 1 ) {a(x_1,y_1,z_1)} a(x1,y1,z1) 与点 b ( x 2 , y 2 , z 2 ) {b(x_2,y_2,z_2)} b(x2,y2,z2) 间的欧式距离
d ( a , b ) = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 {d_{(a,b)}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}} d(a,b)=(x1−x2)2+(y1−y2)2+(z1−z2)2
n维空间点 a ( x 11 , x 12 , … , x 1 n ) {a(x_{11},x_{12},…,x_{1n})} a(x11,x12,…,x1n)与 b ( x 21 , x 22 , … , x 2 n ) {b(x_{21},x_{22},…,x_{2n})} b(x21,x22,…,x2n)间的欧氏距离(两个n维向量)
d ( a , b ) = ∑ k = 1 n ( x 1 k − x 2 k ) 2 {d_{(a,b)}=\sqrt{\sum_{k=1}^n(x_{1k}-x_{2k})^2}} d(a,b)=k=1∑n(x1k−x2k)2
- Python代码
import numpy as np
# 欧氏距离
def EuclideanDistance(x, y):
x = np.array(x)
y = np.array(y)
return np.sqrt(np.sum(np.square(x-y)))
2.2 曼哈顿距离(Manhattan Distance )
| 曼哈顿距离:在曼哈顿街区从一个十字路口开车到另一个十字路口,其中的实际驾驶距离就是“曼哈顿距离”,也称为“城市街区距离”(City Block distance) |
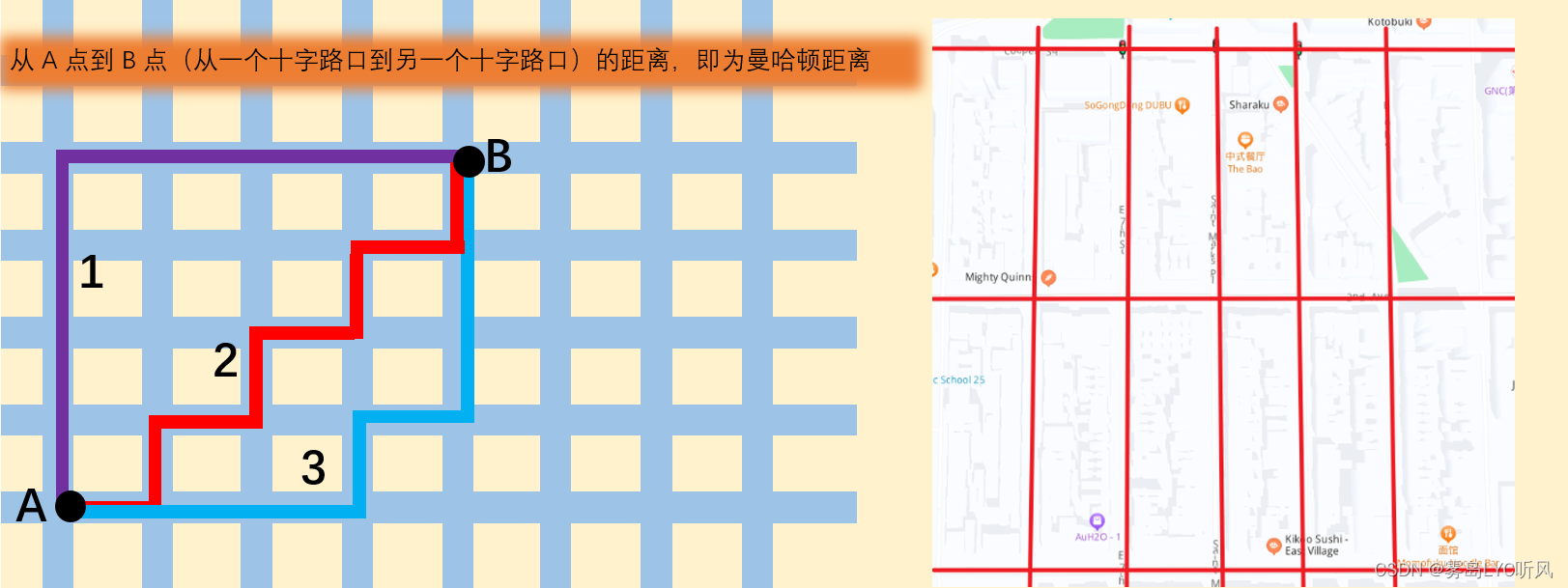
- 数学公式
二维平面两点 a ( x 1 , y 1 ) {a(x_1,y_1)} a(x1,y1) 与点 b ( x 2 , y 2 ) {b(x_2,y_2)} b(x2,y2) 间的曼哈顿距离
d ( a , b ) = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ {d_{(a,b)}=|x_1-x_2|+|y_1-y_2|} d(a,b)=∣x1−x2∣+∣y1−y2∣
n维空间点 a ( x 11 , x 12 , … , x 1 n ) {a(x_{11},x_{12},…,x_{1n})} a(x11,x12,…,x1n)与 b ( x 21 , x 22 , … , x 2 n ) {b(x_{21},x_{22},…,x_{2n})} b(x21,x22,…,x2n)间的曼哈顿距离
d ( a , b ) = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ {d_{(a,b)}=\sum_{k=1}^n|x_{1k}-x_{2k}|} d(a,b)=k=1∑n∣x1k−x2k∣
- Python代码
import numpy as np
# 曼哈顿距离
def ManhattanDistance(x, y):
x = np.array(x)
y = np.array(y)
return np.sum(np.abs(x-y))
2.3 切比雪夫距离(Chebyshev Distance)
| 切比雪夫距离:向量空间中的一种度量,两个点之间的距离定义是其各坐标数值差绝对值的最大值 在国际象棋棋盘上的切比雪夫距离是指王要从一个位置移至另一个位置需要走的最少步数(国王可以直行,横行,斜行,到相邻的8个位置只需要1步) |
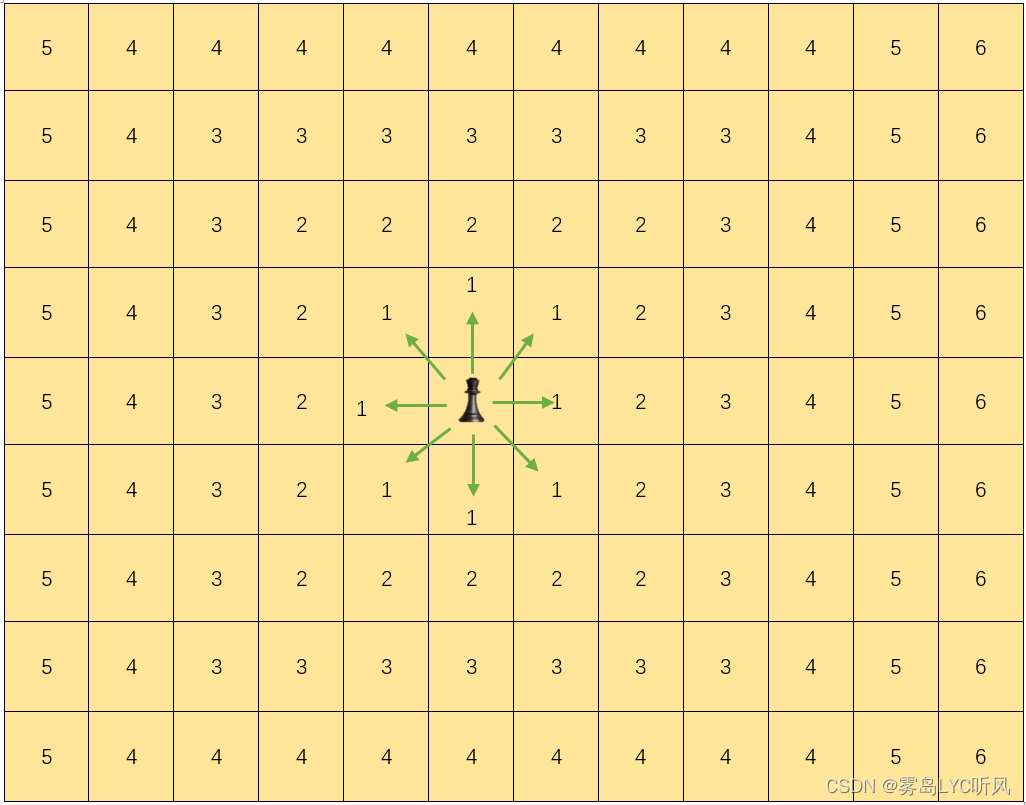
- 数学公式
二维平面两点 a ( x 1 , y 1 ) {a(x_1,y_1)} a(x1,y1) 与点 b ( x 2 , y 2 ) {b(x_2,y_2)} b(x2,y2) 间的切比雪夫距离
d ( a , b ) = m a x ( ∣ x 1 − x 2 ∣ , ∣ y 1 − y 2 ∣ ) {d_{(a,b)}=max(|x_1-x_2|,|y_1-y_2|)} d(a,b)=max(∣x1−x2∣,∣y1−y2∣)
n维空间点 a ( x 11 , x 12 , … , x 1 n ) {a(x_{11},x_{12},…,x_{1n})} a(x11,x12,…,x1n)与 b ( x 21 , x 22 , … , x 2 n ) {b(x_{21},x_{22},…,x_{2n})} b(x21,x22,…,x2n)间的切比雪夫距离
d ( a , b ) = m a x ( ∣ x 1 k − x 2 k ∣ ) {d_{(a,b)}=max(|x_{1k}-x_{2k}|)} d(a,b)=max(∣x1k−x2k∣)
- Python代码
import numpy as np
# 切比雪夫距离
def ChebyshevDistance(x, y):
x = np.array(x)
y = np.array(y)
return np.max(np.abs(x-y))
2.4 闵可夫斯基距离(Minkowski Distance)
| 闵可夫斯基距离:闵可夫斯基距离不是一种距离,而是一组距离的定义(对多个距离度量公式的概括性的表述),即根据变参数p的不同取值,闵氏距离表示一类或是某种距离 缺点 1)将数据的量纲等同看待(即将数据的“单位”看成一样的) 2)为考虑各个分量的分布(期望,方差等) |
- 数学公式
n维空间点 a ( x 11 , x 12 , … , x 1 n ) {a(x_{11},x_{12},…,x_{1n})} a(x11,x12,…,x1n)与 b ( x 21 , x 22 , … , x 2 n ) {b(x_{21},x_{22},…,x_{2n})} b(x21,x22,…,x2n)间的闵可夫斯基距离
d ( a , b ) = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ p p {d_{(a,b)}=\sqrt[p]{\sum_{k=1}^n|x_{1k}-x_{2k}|^p}} d(a,b)=pk=1∑n∣x1k−x2k∣p
其中,p为一个变参数:当 p=1 时,表示曼哈顿距离
当 p=2 时,表示欧氏距离
当 p—> ∞ {\infty} ∞ 时,表示切比雪夫距离
- Python代码
import math
import numpy as np
# 闵可夫斯基距离
def MinkowskiDistance(x, y, p):
zipped_coordinate = zip(x, y)
return math.pow(np.sum([math.pow(np.abs(i[0]-i[1]), p) for i in zipped_coordinate]), 1/p)
2.5 标准化的欧几里得距离(Standardized Euclidean Distance)
| 标准化的欧几里得距离:标准化的欧几里得距离是针对简单欧几里得距离的缺点而作的一种改进方案 |
- 数学公式
思路:将各个分量“标准化”到均值,方差等的区间:
X ∗ = X − m S {X^*={X-m\over S}} X∗=SX−m
其中, X ∗ {X^*} X∗为标准化后的值, X {X} X为原值, m {m} m为分量的均值, S {S} S为分量的标准差
n维空间中标准化的欧几里得距离公式:
d ( a , b ) = ∑ k = 1 n ( x 1 k − x 2 k ) S k ) 2 {d_{(a,b)}=\sqrt{\sum_{k=1}^n{({x_{1k}-x_{2k})}\over S_k)^2}}} d(a,b)=k=1∑nSk)2(x1k−x2k)
如果将方差的导数看成一个权重,则这个公式可以看成是一种加权欧氏距离(Weighted Euclidean Distance)
- Python代码
import numpy as np
# 标准化的欧几里得距离
def StandardizedEuclideanDistance(x, y):
x = np.array(x)
y = np.array(y)
X = np.vstack([x,y])
sigma = np.var(X, axis=0, ddof=1)
return np.sqrt(((x - y) ** 2 /sigma).sum())
2.6 余弦距离(Cosine Distance)
| 余弦距离:也叫余弦相似,几何中夹角余弦可用来衡量两个向量方向的差异(机器学习:衡量样本向量之间的差异),相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上 文本相似性度量:在自然语言处理任务中,余弦距离可用于计算文本之间的相似性 推荐系统:余弦距离可以用于推荐系统中的用户相似性度量 图像处理:在图像处理和计算机视觉中,余弦距离可以用于比较图像特征向量的相似性,如颜色直方图或深度学习特征向量 |
- 数学公式
n nn维空间中的余弦距离:
c o s ( x , y ) = x ⋅ y ∣ x ∣ ⋅ ∣ y ∣ {cos(x,y)={x·y\over |x|·|y|}} cos(x,y)=∣x∣⋅∣y∣x⋅y
即 c o s ( x , y ) = ∑ i = 1 n x i y i ∑ i = 1 n x i 2 ∑ i = 1 n y i 2 {cos(x,y)={\sum_{i=1}^n{x_iy_i}\over \sqrt{\sum_{i=1}^n{x_i^2}}\sqrt{\sum_{i=1}^n{y_i^2}}}} cos(x,y)=∑i=1nxi2∑i=1nyi2∑i=1nxiyi
在机器学习中,经常需要比较和衡量向量之间的相似性或差异性 🢂 余弦距离计算的是两个向量之间的夹角(不仅仅是它们之间的欧氏距离,余弦距离在处理高维数据或稀疏数据时更加有效)
- Python代码
import numpy as np
# 余弦距离
def CosineDistance(x, y):
x = np.array(x)
y = np.array(y)
return np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))
3. K值的选择
| K值的选择 K值过小:容易受到异常点的影响,K值的减小就意味着整体模型变得复杂,易发生过拟合 K值过大:容易受到样本均衡问题的影响,K值增大意味着整体模型变得简单,可能导致欠拟合 K值一般选取一个较小的数值:经验法则 🢂 3或5 交叉验证:使用交叉验证来评估不同的k值对模型的性能产生的影响 网格搜索:使用网格搜索方法在一定范围内尝试不同的k值,并通过交叉验证等评估指标来选择最优的k值 基于问题领域的知识:考虑问题的特点和数据的分布,选择一个与问题相关性较高的k值 |
4. KD树(K-Dimensional Tree)
|
- 构建原理:以2作为根节点(左子树的为小于2的值,右子树的值大于2),中间橙色的分割线为分割超平面
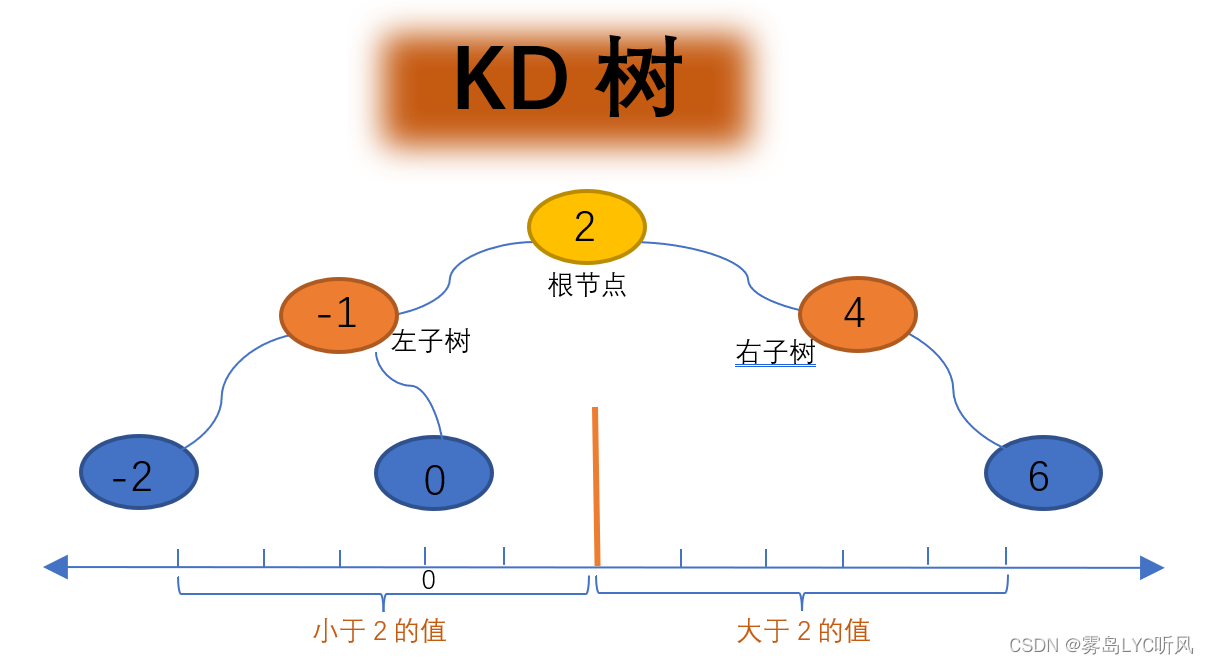
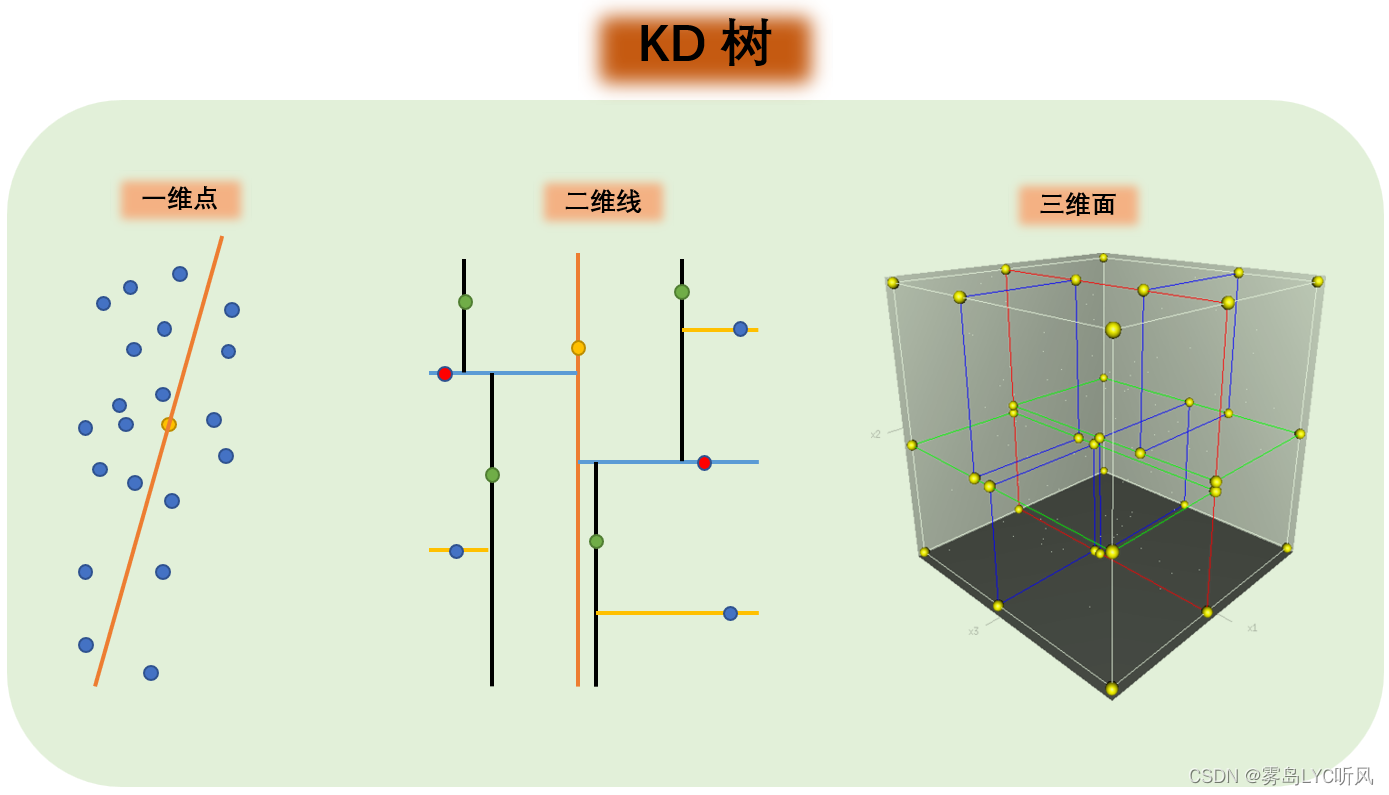
KD树用于优化K近邻算法:由于K近邻算法需要计算待分类样本与所有训练样本之间的距离,当训练集较大时,计算量会变得非常大。而使用KD树可以有效地减少计算量,通过构建KD树结构,在搜索过程中只需要考虑与待分类样本最近邻的子树,避免了对整个训练集的遍历。
KD树的构建和搜索:KD树可以通过递归地将特征空间划分为多个子区域来构建一棵二叉树
KD数的建立
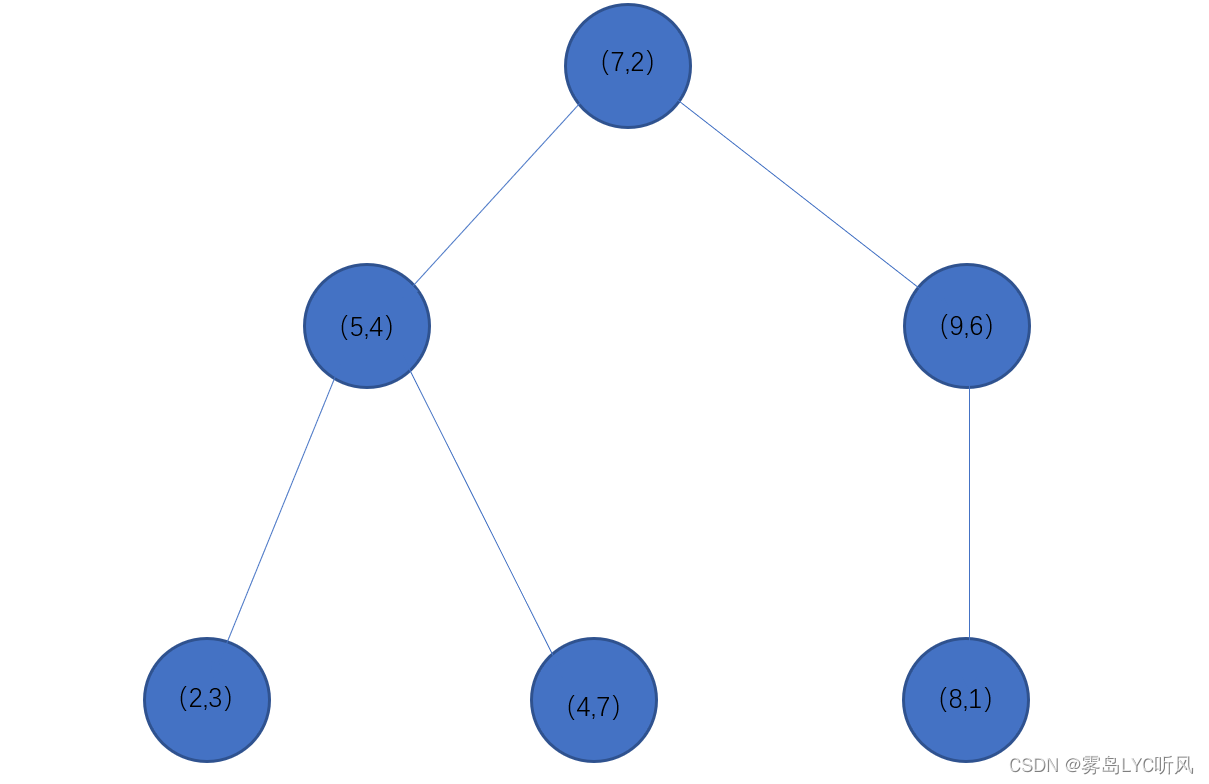
如:有6个点(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)
根节点(此处以中位数确定根节点,如果中位数有两个则可随机选择一个)
先6个点按照不同维度(此处为x,y两个维度)分开进行排序
x轴:2,4,5,7,8,9
y轴:1,2,3,4,5,6
从两个维度中选择一个维度来划分(一般以方差最大化,均值最近邻等来选择先对那个维度划分),如选择方差较大的线划分,第一维度划分完成后,再以此对剩余维度进行划分,直到全部划分完成为止
5. 最近领域搜索(Nearest Neighbor Lookup)
持续更新中***
6. KD树的应用
图像搜索:通过构建KD树,可以将图像数据集中的每个图像表示为一个向量,并且可以高效地进行最近邻搜索。当用户输入一张图像时,可以使用KD树找到与之最相似的图像,实现图像搜索和推荐功能。
机器学习分类:在机器学习中,可以使用KD树来对训练数据进行组织和索引。当有一个新的测试样本需要分类时,可以使用KD树进行最近邻搜索,找到最相似的训练样本,并根据其标签进行分类。
数据库查询优化:在数据库系统中,通过使用KD树索引,可以提高查询的效率。例如,在地理信息系统中,可以使用KD树来索引地理位置信息,通过范围搜索或最近邻搜索快速检索符合条件的数据。
粒子模拟:在计算物理学中,粒子模拟是一种常见的方法,用于模拟物质中的粒子运动。通过使用KD树对粒子进行组织,可以高效地进行粒子之间的相互作用计算,加速模拟过程。
数据压缩:KD树可以用于数据压缩,特别是在高维数据中。通过对数据集进行适当的划分和组织,可以减小数据集的维度并降低存储空间。