原题链接:5180. 正方形泳池 - AcWing题库
说实话题解和视频题解都不太好,有点过于复杂了,那就不得不记录一下我看视频题解衍生出的另一个较为简单的思路了。
根据答案形态出发,枚举所有这种形态找出最大值。

可以发现最大的泳池要么是左右边界被两棵树限制住了,或者就是上下边界被两棵树限制住了。
所以我们可以穷举所有两棵树的组合,并且以这两棵树y的差值或者x的差值为正方形的边长,来放下泳池。最大的泳池,必然在这些组合里面。
放下泳池有限制条件,假设以y的差值放下去,那么可用的连续x也必须大于等于y的差值,两棵树之间可能会有其他树来碍事,那么这里的x就会被断开成好几段,需要找出最大的那个x。
这种只有一棵树的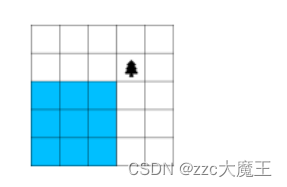 ,因为泳池不能超过边界,所以相当于外面围了一圈树,只要在四个角落种上树就好了。
,因为泳池不能超过边界,所以相当于外面围了一圈树,只要在四个角落种上树就好了。
AC代码
#include <bits/stdc++.h>
using namespace std;
int N,T,ans=INT_MIN;
struct tree{
int x,y;
}t[105];
vector<int>tmp;
bool cmpy(tree a,tree b){
return a.y<b.y;
}
bool cmpx(tree a,tree b){
return a.x<b.x;
}
int main(){
cin>>N>>T;
for(int i=1;i<=T;++i)
cin>>t[i].x>>t[i].y;
t[++T]={0,0};
t[++T]={0,N+1};
t[++T]={N+1,0};
t[++T]={N+1,N+1};
sort(t+1,t+1+T,cmpy);
for(int i=1;i<=T;++i){
for(int j=i+1;j<=T;++j){
tmp.push_back(0);
tmp.push_back(N+1);
for(int k=i+1;k<j;++k)
tmp.push_back(t[k].x);
sort(tmp.begin(),tmp.end());
int xmax=INT_MIN;
for(int k=0;k<tmp.size()-1;++k)
xmax=max(xmax,tmp[k+1]-tmp[k]-1);
ans=max(ans,min(xmax,t[j].y-t[i].y-1));
tmp.clear();
}
}
sort(t+1,t+1+T,cmpx);
for(int i=1;i<=T;++i){
for(int j=i+1;j<=T;++j){
tmp.push_back(0);
tmp.push_back(N+1);
for(int k=i+1;k<j;++k)
tmp.push_back(t[k].y);
sort(tmp.begin(),tmp.end());
int ymax=INT_MIN;
for(int k=0;k<tmp.size()-1;++k)
ymax=max(ymax,tmp[k+1]-tmp[k]-1);
ans=max(ans,min(ymax,t[j].x-t[i].x-1));
tmp.clear();
}
}
cout<<ans<<endl;
return 0;
}思路很简单,但是说也不太说的明白。
重点:枚举所有答案形态。