03-Unsupervised learning
- 3. Unsupervised Learning
- 3.1 无监督学习(Unsupervised Learning)
- 3.1.1 聚类(Clustering)
- 3.1.2 K-均值聚类算法(K-means Clustering)
- 3.1.3 高斯分布(Gaussian distribution)
- 3.1.4 异常检测(Anomaly Detection)
- 3.1.5 异常检测与监督学习
- 3.1.6 选择合适的特征
- 3.2 推荐系统(Recommender Systems)
- 3.2.1 推荐系统与代价函数
- 3.2.2 协同过滤算法(Collaborative Filtering Algorithm)
- 3.2.3 二进制标签(Binary Labels)
- 3.2.4 基于内容过滤算法(Context-based Filtering)以及其与深度学习的结合
- 3.3. 强化学习(Reinforcement Learning)
3. Unsupervised Learning
3.1 无监督学习(Unsupervised Learning)
3.1.1 聚类(Clustering)
在之前的监督学习中,每一组数据都给定了输出值,即为 ( x , y ) (x,y) (x,y)的形态,在无监督学习中,我们不再给定确定的输出值,而由算法来发现数据之间的关系。
聚类算法会尝试将给定的数据确定为多个聚类(clusters)。
3.1.2 K-均值聚类算法(K-means Clustering)
k-均值聚类算法是聚类算法的一种,通过不断计算点与聚类质心的距离来不断分配点所属的聚类,具体步骤如下:
- 随机初始化K个聚类的质心(cluster centroid): μ 1 , μ 2 , . . . , μ K \mu_1,\mu_2,...,\mu_K μ1,μ2,...,μK;
- 假设有m个数据,对每一个数据执行下述操作,用i来标记数据:
- 计算该数据到每个质心的平方距离,并记录使距离最小的质心的下标k,即 m i n k ∣ ∣ x ( i ) − μ k ∣ ∣ 2 min_k ||x^{(i)}-\mu_k||^2 mink∣∣x(i)−μk∣∣2,也被称为L2范数;
- 用下标k标记该点,即 c ( i ) = k c^{(i)}=k c(i)=k;
- 更新聚类质心位置:即遍历上一步中被标记为k的数据,计算这些数据的平均位置,用这个平均位置更新聚类位置;
- 如果有聚类没有被分到数据,一般做法为删除该聚类;
- 返回第二步,直到聚类质心位置收敛(converge)。
为了表达算法的代价函数,引入一些标记:
c ( i ) c^{(i)} c(i):表示测试样本 x ( i ) x^{(i)} x(i)当前所属的聚类的下标;
μ k \mu_k μk:表示聚类k的质心位置;
μ c ( i ) \mu_{c^{(i)}} μc(i):表示测试样本 x ( i ) x^{(i)} x(i)当前所属的聚类的质心位置。
然后就可以定义K-均值聚类算法的代价函数,代价函数
J
J
J在文献中也被称为失真函数(distortion function)。
J
(
c
(
1
)
,
.
.
.
,
c
(
m
)
,
μ
1
,
.
.
.
,
μ
K
)
=
1
m
∑
i
=
1
m
∣
∣
x
(
i
)
−
μ
c
(
i
)
∣
∣
2
J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K)= \frac{1}{m} \sum_{i=1}^m || x^{(i)} - \mu_{c^{(i)}} ||^2
J(c(1),...,c(m),μ1,...,μK)=m1i=1∑m∣∣x(i)−μc(i)∣∣2
J也被称为失真(distortion)函数。
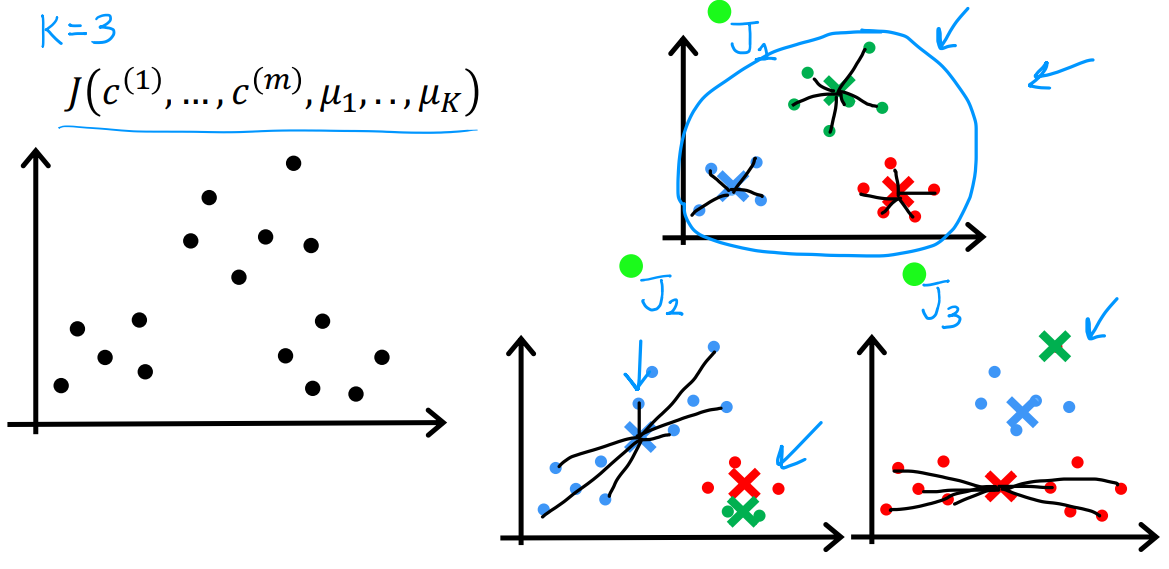
但是如何初始化聚类的质心呢?在坐标轴上任意随机显然不明智。我们通常随机选择训练集中的某些数据作为初始坐标。以下图为例,我们尝试找到三个聚类,但是由于初始化是随机的,可能拟合出不好的聚类,这就需要计算每个拟合结果的代价函数,选择最小的作为结果,即选用 J 1 J_1 J1。常见的循环次数是50-1000次。
此外,应该如何选择合适的聚类数量呢?
在具体的应用当中,可以根据情景需求确定聚类数量,比如在T恤衫型号案例中,如果我们希望得到S、M、L三种型号,那么K就应该选择为3,如果希望得到更详细的XS、S、M、L、XL五种型号,那么K就应该被选择为5。
3.1.3 高斯分布(Gaussian distribution)
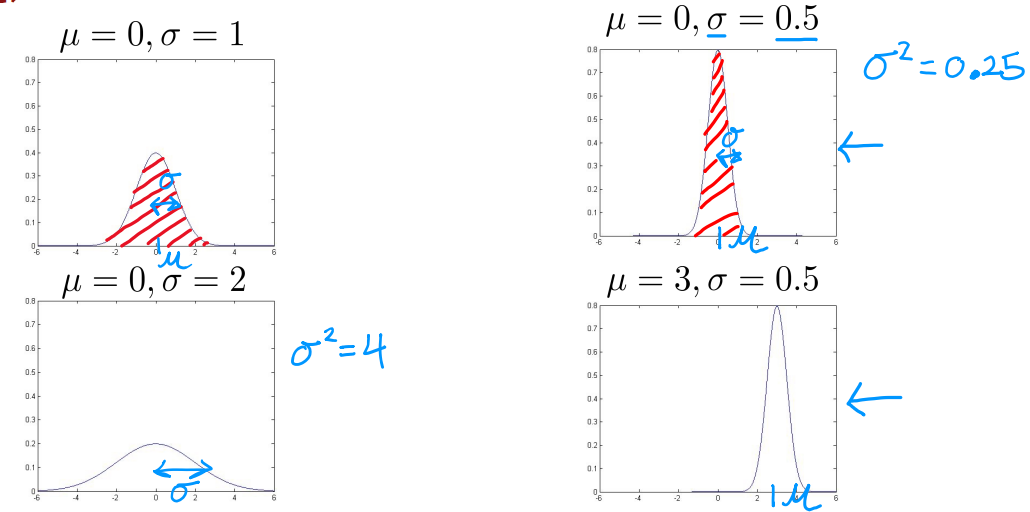
高斯分布(Gaussian distribution),也被称为正态分布(Normal distribution)。若随机变量 X X X服从一个数学期望为 μ μ μ、方差为 σ 2 σ^2 σ2的正态分布,记为 N ( μ , σ 2 ) N(μ,σ^2) N(μ,σ2)。其概率密度函数为正态分布的期望值** μ μ μ决定了其位置,其标准差 σ σ σ决定了分布的幅度**。
当 μ = 0 , σ = 1 μ = 0,σ = 1 μ=0,σ=1时的正态分布是标准正态分布。由于概率之和为1,所以图像面积也为1。
正态分布的公式为:
p
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
2
σ
2
p(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{\frac{-(x-\mu)^2}{2\sigma^2}}
p(x)=2πσ1e2σ2−(x−μ)2
其中,数学期望
μ
μ
μ、方差
σ
2
σ^2
σ2计算方法是:
μ
=
1
m
∑
i
=
1
m
x
(
i
)
,
σ
2
=
1
m
∑
i
=
1
m
(
x
(
i
)
−
μ
)
2
\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)}, \sigma^2 = \frac{1}{m} \sum_{i=1}^m (x^{(i)} - \mu)^2
μ=m1i=1∑mx(i),σ2=m1i=1∑m(x(i)−μ)2
3.1.4 异常检测(Anomaly Detection)
异常检测是根据已有的数据集,对新测试数据进行判断,监控相对已有数据,新数据是否不符合原数据的标准。进行异常检测最常见的方法是密度估计(density estimation)。
对于测试集 { x ( 1 ) , x ( 2 ) , . . . , x ( m ) } \{ x^{(1)},x^{(2)},...,x^{(m)} \} {x(1),x(2),...,x(m)},其中每一个样本 x ( i ) x^{(i)} x(i)都有n个特征,即 x ( i ) = [ x 1 , x 2 , . . . , x n ] x^{(i)} = [ x_1,x_2,...,x_n ] x(i)=[x1,x2,...,xn]。根据正态分布,得到下面的公式。
p ( x ⃗ ) = p ( x 1 ; μ 1 , σ 1 2 ) ∗ p ( x 2 ; μ 2 , σ 2 2 ) ∗ p ( x 3 ; μ 3 , σ 3 2 ) ∗ . . . ∗ p ( x n ; μ n , σ n 2 ) = ∏ j = 1 n p ( x j ; μ j , σ j 2 ) p(\vec{x}) = p(x_1;\mu_1,\sigma_1^2) *p(x_2;\mu_2,\sigma_2^2) *p(x_3;\mu_3,\sigma_3^2) *...*p(x_n;\mu_n,\sigma_n^2) =\prod_{j=1}^n p(x_j;\mu_j,\sigma_j^2) p(x)=p(x1;μ1,σ12)∗p(x2;μ2,σ22)∗p(x3;μ3,σ32)∗...∗p(xn;μn,σn2)=j=1∏np(xj;μj,σj2)
进一步得到异常检测算法的步骤:
-
选择n个可能指示出异常的特征;
-
拟合参数 μ 1 , . . . , μ n , σ 1 2 , . . . , σ n 2 \mu_1,...,\mu_n,\sigma_1^2,...,\sigma_n^2 μ1,...,μn,σ12,...,σn2,其中 μ j = 1 m ∑ i = 1 m x j ( i ) , σ j 2 = 1 m ∑ i = 1 m ( x j ( i ) − μ j ) 2 \mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)}, \sigma_j^2 = \frac{1}{m} \sum_{i=1}^m (x_j^{(i)} - \mu_j)^2 μj=m1∑i=1mxj(i),σj2=m1∑i=1m(xj(i)−μj)2;
针对参数的计算也有向量化的表达: μ ⃗ = 1 m ∑ i = 1 m x ⃗ ( i ) = [ μ 1 , μ 2 , . . . , μ n ] \vec{\mu} = \frac{1}{m} \sum_{i=1}^m \vec{x}^{(i)} = [\mu_1,\mu_2,...,\mu_n] μ=m1∑i=1mx(i)=[μ1,μ2,...,μn];
-
给定一个测试样本 x x x,计算 p ( x ) p(x) p(x),即:
p ( x ) = ∏ j = 1 n p ( x j ; μ j , σ j 2 ) = ∏ j = 1 n 1 2 π σ j e − ( x j − μ j ) 2 2 σ j 2 p(x) = \prod_{j=1}^n p(x_j;\mu_j,\sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2\pi}\sigma_j} e^{\frac{-(x_j-\mu_j)^2}{2\sigma_j^2}} p(x)=j=1∏np(xj;μj,σj2)=j=1∏n2πσj1e2σj2−(xj−μj)2 -
最后判断 p ( x ) p(x) p(x)与 ϵ \epsilon ϵ的大小关系。
3.1.5 异常检测与监督学习
异常检测与监督学习的使用场景:
| 异常检测 | 监督学习 |
|---|---|
| 异常样本(y=1)数量很少,通常是0-20个 | 大量异常样本,通常大于20个 |
| 大量非异常样本(y=0) | 大量非异常样本 |
| 异常的类型很多,未来出现的异常可能与迄今为止看到的任何异常情况都不一样,即变数很大 | 有足够多的异常样本让算法知道异常样本是什么样的。未来的异常可能与训练集中的异常相似 |
异常检测与监督学习的使用举例:
| 异常检测 | 监督学习 |
|---|---|
| 金融诈骗 | 垃圾邮件分类 |
| 制造业,比如需要找到新的无法预知的缺陷 | 制造业,比如找到已有的缺陷 |
| 监控数据中心中的机器,比如防黑客入侵 | 天气预报、疾病分类 |
3.1.6 选择合适的特征
在监督学习中,如果没有选好训练集特征,运行结果通常也不会受很大影响,因为样本有监督信号,让算法找出需要被忽略的特征,或者调整特征,但对于没有标记数据的异常检测算法(无监督学习),则很难找出需要被忽略的训练集特征。所以异常检测更需要谨慎挑选特征。
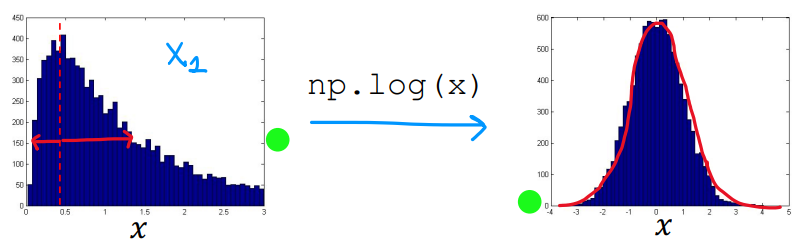
选择合适特征应当注意的是,训练集特征给出的数据通常符合正态分布。我们可以通过Python库绘制值的图像,如果是类似左图中不对称的分布,可以通过线性变换使之更加贴合正态分布,比如取对数,改为幂函数(如平方根)。
但无论对训练集特征使用了什么样的转换,交叉验证集和测试集也需要进行同样的变换。
3.2 推荐系统(Recommender Systems)
3.2.1 推荐系统与代价函数
推荐系统(Recommender Systems)是极具商业价值的机器学习算法,生活中很多系统都采用推荐系统来给他们的用户推荐可能喜欢的东西。
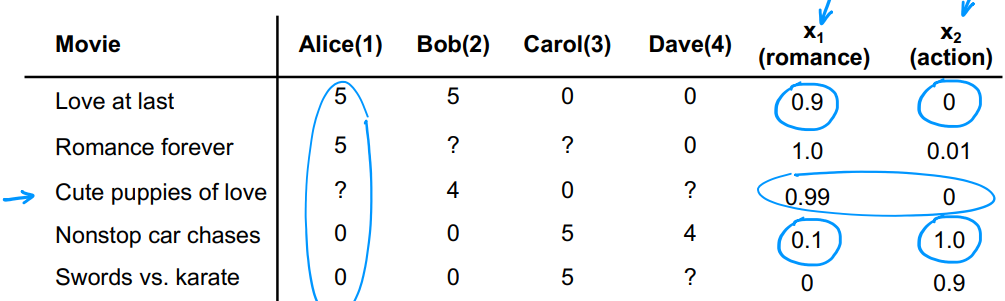
以图中电影推荐系统为例,数字表示某人给某电影打了多少分,问号表示该用户暂未观看该电影。我们用 n u n_u nu表示用户总数,用 n m n_m nm表示电影总数,则有 n u = 4 、 n m = 5 n_u =4、n_m=5 nu=4、nm=5。用 r ( i , j ) = 0 , 1 r(i,j)=0,1 r(i,j)=0,1来表示** i i i号用户是否给 j j j号电影打了分**,用 y ( i , j ) = 0 , 1 , 2 , 3 , 4 , 5 y^{(i,j)}=0,1,2,3,4,5 y(i,j)=0,1,2,3,4,5表示用户实际打了多少分。表中最右边两列表示电影的特征,引入 n n n表示电影的特征数量,则有 n = 2 n=2 n=2。用 x ( i ) = [ . . . ] x^{(i)}=[...] x(i)=[...]表示** i i i号电影的特征**,如1号电影就有 x ( 1 ) = [ 0.9 , 0 ] x^{(1)}=[0.9,0] x(1)=[0.9,0]。
用类线性回归模型预测用户 i i i对电影 j j j的喜好程度: w ( i ) ⋅ x ( j ) + b ( i ) w^{(i)}·x^{(j)}+b^{(i)} w(i)⋅x(j)+b(i)。其中** w ( i ) w^{(i)} w(i)和 b ( i ) b^{(i)} b(i)是用户 i i i的参数**。
现在来预测1号用户Alice对3号电影的感兴趣程度,即计算 y ^ ( 1 , 3 ) \hat{y}^{(1,3)} y^(1,3):表中已知 y ( 1 , 1 ) = 5 、 y ( 1 , 4 ) = 0 y^{(1,1)}=5、y^{(1,4)}=0 y(1,1)=5、y(1,4)=0,则 w ( 1 ) = [ 5 , 0 ] w^{(1)}=[5,0] w(1)=[5,0]。且 x ( 3 ) = [ 0.99 , 0 ] x^{(3)}=[0.99,0] x(3)=[0.99,0],令 b ( i ) = 0 b^{(i)}=0 b(i)=0,有 y ^ ( 1 , 3 ) = w ( 1 ) ⋅ x ( 3 ) + b ( 1 ) = 4.95 \hat{y}^{(1,3)}=w^{(1)}·x^{(3)}+b^{(1)}=4.95 y^(1,3)=w(1)⋅x(3)+b(1)=4.95,所以可能打4.95分。
推荐系统同样也有代价函数,引入 m ( i ) m^{(i)} m(i)表示用户i给多少部电影打了分, w ( i ) w^{(i)} w(i)和 b ( i ) b^{(i)} b(i)是算法需要预测的用户参数。对于用户i看过的每一部电影,第一项针对所有电影估算用户i会给出的分数,累计代价并求平均代价。第二项用于正则化参数,防止过拟合。
J ( w ( i ) , b ( i ) ) = 1 2 m ( i ) ∑ j : r ( i , j ) = 1 j = n m ( w ( i ) ⋅ x ( j ) + b ( i ) − y ( i , j ) ) 2 + λ 2 m ( i ) ∑ k = 1 n ( w k ( i ) ) 2 a n d m i n w ( i ) , b ( i ) J ( w ( i ) , b ( i ) ) J(w^{(i)},b^{(i)}) = \frac{1}{2m^{(i)}} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \frac{\lambda}{2m^{(i)}} \sum_{k=1}^{n} ( w_k^{(i)} )^2 \\and \\min_{w^{(i)},b^{(i)}} J(w^{(i)},b^{(i)}) J(w(i),b(i))=2m(i)1j:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+2m(i)λk=1∑n(wk(i))2andminw(i),b(i)J(w(i),b(i))
但是 m ( i ) m^{(i)} m(i)是一个常数,对计算没有影响,可以省略,于是用户i的代价函数最终为:
J
(
w
(
i
)
,
b
(
i
)
)
=
1
2
∑
j
:
r
(
i
,
j
)
=
1
j
=
n
m
(
w
(
i
)
⋅
x
(
j
)
+
b
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
k
=
1
n
(
w
k
(
i
)
)
2
J(w^{(i)},b^{(i)}) = \frac{1}{2} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \frac{\lambda}{2} \sum_{k=1}^{n} ( w_k^{(i)} )^2
J(w(i),b(i))=21j:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+2λk=1∑n(wk(i))2
对于系统中的所有用户,所有用户的代价函数就是:
J
(
w
(
1
)
,
b
(
1
)
;
.
.
.
;
w
(
i
)
,
b
(
i
)
)
=
1
2
∑
i
=
1
n
u
∑
j
:
r
(
i
,
j
)
=
1
j
=
n
m
(
w
(
i
)
⋅
x
(
j
)
+
b
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
i
=
1
n
u
∑
k
=
1
n
(
w
k
(
i
)
)
2
J(w^{(1)},b^{(1)};...;w^{(i)},b^{(i)}) = \frac{1}{2} \sum_{i=1}^{n_u} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \frac{\lambda}{2} \sum_{i=1}^{n_u} \sum_{k=1}^{n} ( w_k^{(i)} )^2
J(w(1),b(1);...;w(i),b(i))=21i=1∑nuj:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+2λi=1∑nuk=1∑n(wk(i))2
3.2.2 协同过滤算法(Collaborative Filtering Algorithm)
上一节的案例中,给定了每一部电影的特征 x 1 x_1 x1和 x 2 x_2 x2,如果现实应用中没有这些特征,就要从数据中学习或提取这些特征。
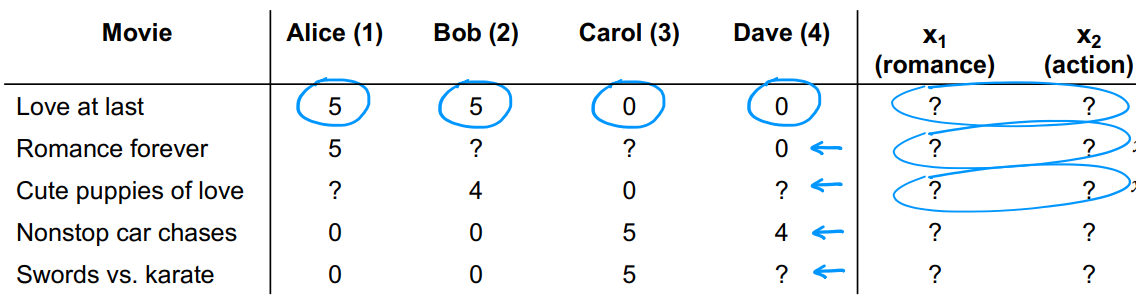
假定已知所有用户参数,且 w ( 1 ) = [ 5 , 0 ] w^{(1)}=[5,0] w(1)=[5,0]、 w ( 2 ) = [ 5 , 0 ] w^{(2)}=[5,0] w(2)=[5,0]、 w ( 3 ) = [ 0 , 5 ] w^{(3)}=[0,5] w(3)=[0,5]、 w ( 4 ) = [ 0 , 5 ] w^{(4)}=[0,5] w(4)=[0,5],并置 b ( 1 ) = b ( 2 ) = b ( 3 ) = b ( 4 ) = 0 b^{(1)}=b^{(2)}=b^{(3)}=b^{(4)}=0 b(1)=b(2)=b(3)=b(4)=0,继续使用公式 w ( i ) ⋅ x ( j ) + b ( i ) w^{(i)}·x^{(j)}+b^{(i)} w(i)⋅x(j)+b(i)。
以第一部电影为例,所有用户评分已知,则有: w ( 1 ) ⋅ x ( 1 ) ≈ 5 w^{(1)}·x^{(1)} \approx 5 w(1)⋅x(1)≈5、 w ( 2 ) ⋅ x ( 1 ) ≈ 5 w^{(2)}·x^{(1)} \approx 5 w(2)⋅x(1)≈5、 w ( 3 ) ⋅ x ( 1 ) ≈ 0 w^{(3)}·x^{(1)} \approx 0 w(3)⋅x(1)≈0、 w ( 4 ) ⋅ x ( 1 ) ≈ 0 w^{(4)}·x^{(1)} \approx 0 w(4)⋅x(1)≈0。故可以估计 x ( 1 ) = [ 5 , 0 ] x^{(1)}=[5,0] x(1)=[5,0]。
针对这样的计算同样也有代价函数,求平均值的参数同样可以省略,即:
J
(
x
(
i
)
)
=
1
2
∑
j
:
r
(
i
,
j
)
=
1
j
=
n
m
(
w
(
i
)
⋅
x
(
j
)
+
b
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
k
=
1
n
(
x
k
(
i
)
)
2
J(x^{(i)}) = \frac{1}{2} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \frac{\lambda}{2} \sum_{k=1}^{n} ( x_k^{(i)} )^2
J(x(i))=21j:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+2λk=1∑n(xk(i))2
类似的,对于每一部电影的所有特征,所有用户的代价函数就是:
J
(
x
(
1
)
,
.
.
.
,
x
(
i
)
)
=
1
2
∑
i
=
1
n
u
∑
j
:
r
(
i
,
j
)
=
1
j
=
n
m
(
w
(
i
)
⋅
x
(
j
)
+
b
(
i
)
−
y
(
i
,
j
)
)
2
+
∑
i
=
1
n
u
λ
2
∑
k
=
1
n
(
x
k
(
i
)
)
2
J(x^{(1)},...,x^{(i)}) = \frac{1}{2} \sum_{i=1}^{n_u} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \sum_{i=1}^{n_u} \frac{\lambda}{2} \sum_{k=1}^{n} ( x_k^{(i)} )^2
J(x(1),...,x(i))=21i=1∑nuj:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+i=1∑nu2λk=1∑n(xk(i))2
上文中的两次计算,第一次给定电影特征,估计用户参数;第二次给定用户参数,估计电影特征。但不难发现,第一项其实是相同的,我们可以将两式结合,同时对用户参数和电影特征进行拟合,这也称为协同过滤(Collaborative Filtering),结合后的式子为:
J
(
w
,
b
,
x
)
=
1
2
∑
i
=
1
n
u
∑
j
:
r
(
i
,
j
)
=
1
j
=
n
m
(
w
(
i
)
⋅
x
(
j
)
+
b
(
i
)
−
y
(
i
,
j
)
)
2
+
λ
2
∑
i
=
1
n
u
∑
k
=
1
n
(
w
k
(
i
)
)
2
+
∑
i
=
1
n
u
λ
2
∑
k
=
1
n
(
x
k
(
i
)
)
2
J(w,b,x) = \frac{1}{2} \sum_{i=1}^{n_u} \sum_{j:r(i,j)=1}^{j=n_m} ( w^{(i)}·x^{(j)}+b^{(i)}-y^{(i,j)} )^2+ \frac{\lambda}{2} \sum_{i=1}^{n_u} \sum_{k=1}^{n} ( w_k^{(i)} )^2+ \sum_{i=1}^{n_u} \frac{\lambda}{2} \sum_{k=1}^{n} ( x_k^{(i)} )^2
J(w,b,x)=21i=1∑nuj:r(i,j)=1∑j=nm(w(i)⋅x(j)+b(i)−y(i,j))2+2λi=1∑nuk=1∑n(wk(i))2+i=1∑nu2λk=1∑n(xk(i))2
如果要对w、b、x进行最小化,我们可以使用梯度下降法(Gradient Descent),其中k表示分量,w、b、x现在都是参数。
r
e
p
e
a
t
{
w
k
(
i
)
=
w
k
(
i
)
−
α
∂
∂
w
k
(
i
)
J
(
w
,
b
,
x
)
b
(
i
)
=
b
(
i
)
−
α
∂
∂
b
(
i
)
J
(
w
,
b
,
x
)
x
k
(
j
)
=
x
k
(
j
)
−
α
∂
∂
x
k
(
j
)
J
(
w
,
b
,
x
)
}
s
i
m
u
l
t
a
n
e
o
u
s
u
p
d
a
t
e
s
\begin{align} & repeat\{ \\ &\qquad w_k^{(i)} = w_k^{(i)} - α \frac{∂}{∂w_k^{(i)}}J(w,b,x)\\ &\qquad b^{(i)} = b^{(i)} - α \frac{∂}{∂b^{(i)}}J(w,b,x)\\ &\qquad x_k^{(j)} = x_k^{(j)} - α \frac{∂}{∂x_k^{(j)}}J(w,b,x)\\ & \}simultaneous \quad updates \end{align}
repeat{wk(i)=wk(i)−α∂wk(i)∂J(w,b,x)b(i)=b(i)−α∂b(i)∂J(w,b,x)xk(j)=xk(j)−α∂xk(j)∂J(w,b,x)}simultaneousupdates
3.2.3 二进制标签(Binary Labels)
具体的实例有时可能不是0-5星的评分,而是0或1的二元分类,分别表示没有看过和看过,这样问题就变成了一个逻辑回归模型,我们可以利用之前的协同过滤算法来进行计算,判断某位用户是否会对某个没有看过的电影感兴趣,并用0或者1来表示。
我们之前使用 y ( i , j ) = w ( i ) ⋅ x ( j ) + b ( i ) y^{(i,j)} = w^{(i)}·x^{(j)}+b^{(i)} y(i,j)=w(i)⋅x(j)+b(i)来进行预测,其中 y ( i , j ) y^{(i,j)} y(i,j)表示用户i是否看过电影j。
如果是逻辑回归的话,就会变成 g ( w ( i ) ⋅ x ( j ) + b ( i ) ) g(w^{(i)}·x^{(j)}+b^{(i)}) g(w(i)⋅x(j)+b(i)),并且 g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1。
根据之前的知识,可以得到新的损失(loss)函数和代价函数为:
L
(
f
(
w
,
b
,
x
)
(
x
)
,
y
(
i
,
j
)
)
=
−
y
(
i
,
j
)
l
o
g
(
f
(
w
,
b
,
x
)
(
x
)
)
−
(
1
−
y
(
i
,
j
)
)
l
o
g
(
1
−
f
(
w
,
b
,
x
)
(
x
)
)
J
(
w
,
b
,
x
)
=
∑
(
i
,
j
)
:
r
(
i
,
j
)
=
1
L
(
f
(
w
,
b
,
x
)
(
x
)
,
y
(
i
,
j
)
)
L( f_{(w,b,x)}(x), y^{(i,j)}) = -y^{(i,j)}log(f_{(w,b,x)}(x)) - (1-y^{(i,j)})log(1 - f_{(w,b,x)}(x)) \\ J(w,b,x) = \sum_{(i,j):r(i,j)=1} L( f_{(w,b,x)}(x), y^{(i,j)})
L(f(w,b,x)(x),y(i,j))=−y(i,j)log(f(w,b,x)(x))−(1−y(i,j))log(1−f(w,b,x)(x))J(w,b,x)=(i,j):r(i,j)=1∑L(f(w,b,x)(x),y(i,j))
3.2.4 基于内容过滤算法(Context-based Filtering)以及其与深度学习的结合
协同过滤算法基于和用户给出相似分数的其他用户来推荐项目;而基于内容过滤算法则基于用户特征和项目本身来推荐项目。
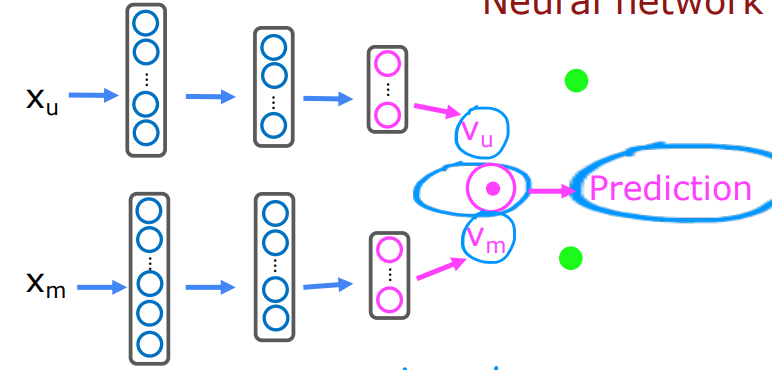
比如用户特征User features可能包含:Age、Gender、Country、Movies watched、Average rating per genre等,这些特征组合为了用户j的特征向量 x u ( j ) x_u^{(j)} xu(j);电影特征Movie features可能包含:Year、Genre/Genres、Reviews、Average rating等,这些特征组合为了电影i的特征向量 x m ( i ) x_m^{(i)} xm(i)。这两个向量的长度可能是不同的。
我们期望通过这两个向量来估计用户j给电影i的评分,这通过向量的点乘运算可以得到,比如:用户向量 v u ( j ) = [ 4.9 , 0.1 , . . . ] v_u^{(j)}=[4.9,0.1,...] vu(j)=[4.9,0.1,...],每个元素分别表示该用户对浪漫电影的评分、对动作电影的评分;电影向量 v m ( i ) = [ 4.5 , 0.2 , . . . ] v_m^{(i)}=[4.5,0.2,...] vm(i)=[4.5,0.2,...],分别表示该电影属于浪漫类的指数、属于动作类的指数。我们可以对这两个向量进行点乘来计算用户可能给出的评分,并且可以进行某种规格化使评分控制在0-5分范围内。
但是之前的 x u ( j ) x_u^{(j)} xu(j)和 x m ( i ) x_m^{(i)} xm(i)的长度可能不同,我们无法对长度不同的向量做点乘运算,此时可以利用神经网络生成长度相同的向量。然后对新向量进行点乘运算来完成预测。可以进一步得到代价函数为 J = ∑ ( i , j ) : r ( i , j ) = 1 ( v u ( j ) ⋅ v m ( i ) − y ( i , j ) ) 2 J = \sum_{(i,j):r(i,j)=1}(v_u^{(j)}·v_m^{(i)} - y^{(i,j)})^2 J=∑(i,j):r(i,j)=1(vu(j)⋅vm(i)−y(i,j))2。