【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
目前机器人常用的搜路算法主要有这么几种,迪杰斯特拉算法、a*算法、贪心算法。每一种算法都有自己的场景和优势,可以灵活选择。但一般来说,客户的场景不算很复杂的话,搜路算法越简单越好,只要能达到最终的目标即可。对于特别复杂的场景,建议也不要通过底层算法的变更来解决业务的问题,这反而是得不偿失的。所以说,这三种算法,如果没有特别原因的话,最好都实现一下,这样方便fae的同学现场部署和实施。搜路算法本身只是一个拓扑算法,它帮助我们分析了目的地本身是否可达,但是机器人能不能过去,这就两说了。
下面,我们就看下a*算法是怎么实现的。
1、a*算法的核心
a*算法的核心其实就是F=G+H。其中F是总代价,G是起始点到当前点的代价,H是当前点到目标点的代价。两者加在一起,就是每次选择新插入点的标准。
2、a*算法的流程
a*算法的伪代码流程一般是这样的,
1)将开始点设置为p;
2)p点插入到封闭集当中;
3)搜寻p的所有邻接点,如果邻接点没有在开放集或者封闭集之中,则计算该点的F值,设置该邻接点的parent为p,将临界点插入到开放集当中;
4)判断开放集是否为空,如果为空,则搜路失败,否则继续;
5)从开放集挑出F数值最小的点,作为寻路的下一步起始点;
6)判断该点是否是终点,如果是,结束查找,否则继续;
7)跳转到3继续执行。
3、a*算法的注意事项
整个a*算法还是不算太复杂的。需要注意的地方只有一处,那就是3)中如果发现邻接点已经在开放集中,那需要重新计算它的G值。一旦发现当前G值更小,则需要同步更新parent、G值和F值。
4、测试代码
算法的整个过程参考了一本ROS参考书上的python代码。大家可以实际下载下来查看一下效果。代码是用python编写,需要安装matplotlib库。
import matplotlib.pyplot as plt
import math
class Node:
def __init__(self, x, y, parent, cost, index):
self.x =x
self.y = y
self.parent = parent
self.cost = cost
self.index = index
def calc_path(goaln, closeset):
rx,ry = [goaln.x], [goaln.y]
print(closeset[-1])
parentn = closeset[-1]
while parentn != None:
rx.append(parentn.x)
ry.append(parentn.y)
parentn = parentn.parent
return rx, ry
def astar_plan(sx, sy, gx, gy):
ox,oy,xwidth,ywidth = map_generation()
plt.figure('Astar algorithm')
plt.plot(ox, oy, 'ks')
plt.plot(sx, sy, 'bs')
plt.plot(gx, gy, 'ro')
motion = motion_model()
openset, closeset = dict(), dict()
sidx = sy*xwidth + sx
gidx = gy*xwidth + gx
starn = Node(sx, sy, None, 0, sidx)
goaln = Node(gx, gy, None, 0, gidx)
openset[sidx] = starn
while 1:
c_id = min(openset,key=lambda o:openset[o].cost + h_cost(openset[o], goaln))
curnode = openset[c_id]
if curnode.x == goaln.x and curnode.y == goaln.y:
print('find goal')
closeset[-1] = curnode
break
else:
closeset[c_id] = curnode
plt.plot(curnode.x, curnode.y, 'gx')
if len(openset.keys())%10 == 0:
plt.pause(0.01)
del openset[c_id]
for j in range(len(motion)):
newnode = Node(curnode.x + motion[j][0],
curnode.y + motion[j][1],
curnode,
curnode.cost + motion[j][2],
c_id)
n_id = index_calc(newnode, xwidth)
if n_id in closeset:
continue
if node_verify(newnode, ox, oy):
continue
if n_id not in openset:
openset[n_id] = newnode
else:
if openset[n_id].cost >= newnode.cost:
openset[n_id] = newnode
px,py = calc_path(goaln, closeset)
return px,py
def map_generation():
ox,oy=[],[]
for i in range(60):
ox.append(i)
oy.append(0)
for i in range(60):
ox.append(i)
oy.append(60)
for i in range(60):
ox.append(0)
oy.append(i)
for i in range(60):
ox.append(60)
oy.append(i)
for i in range(25):
ox.append(i)
oy.append(20)
for i in range(40):
ox.append(35)
oy.append(i)
for i in range(40):
ox.append(50)
oy.append(60-i)
minx = min(ox)
miny = min(oy)
maxx = max(ox)
maxy = max(oy)
xwidth = maxx-minx
ywidth = maxy-miny
return ox,oy,xwidth,ywidth
def motion_model():
motion= [[1,0,1],
[1,1,math.sqrt(2)],
[1,-1,math.sqrt(2)],
[0,1,1],
[0,-1,1],
[-1,1,math.sqrt(2)],
[-1,0,1],
[-1,-1,math.sqrt(2)]
]
return motion
def h_cost(node, goal):
w = 1.0
h = w * (abs(goal.x-node.x) + abs(goal.y-node.y))
return h
def index_calc(node, xwid):
n_id = node.y * xwid + node.x
return n_id
def node_verify(node, ox, oy):
if(node.x, node.y) in zip(ox, oy):
return True
else:
return False
def main():
sx,sy=15,15
gx,gy=55,50
rx,ry=astar_plan(sx,sy,gx,gy)
print(rx,ry)
plt.plot(rx,ry,'r-',linewidth=3)
plt.show()
if __name__ == '__main__':
main()
代码中motion_model表示了当前点周围8个点的行驶代价;node_verify则是判断当前点是否在障碍物上;astar_plan是所有算法真正的入口;而map_generation则构建了一个基本的搜寻场景。
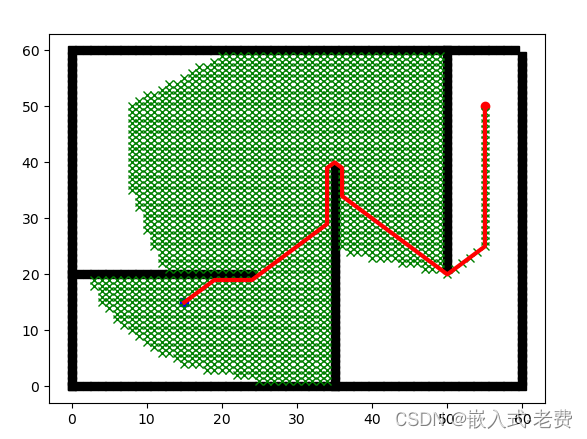
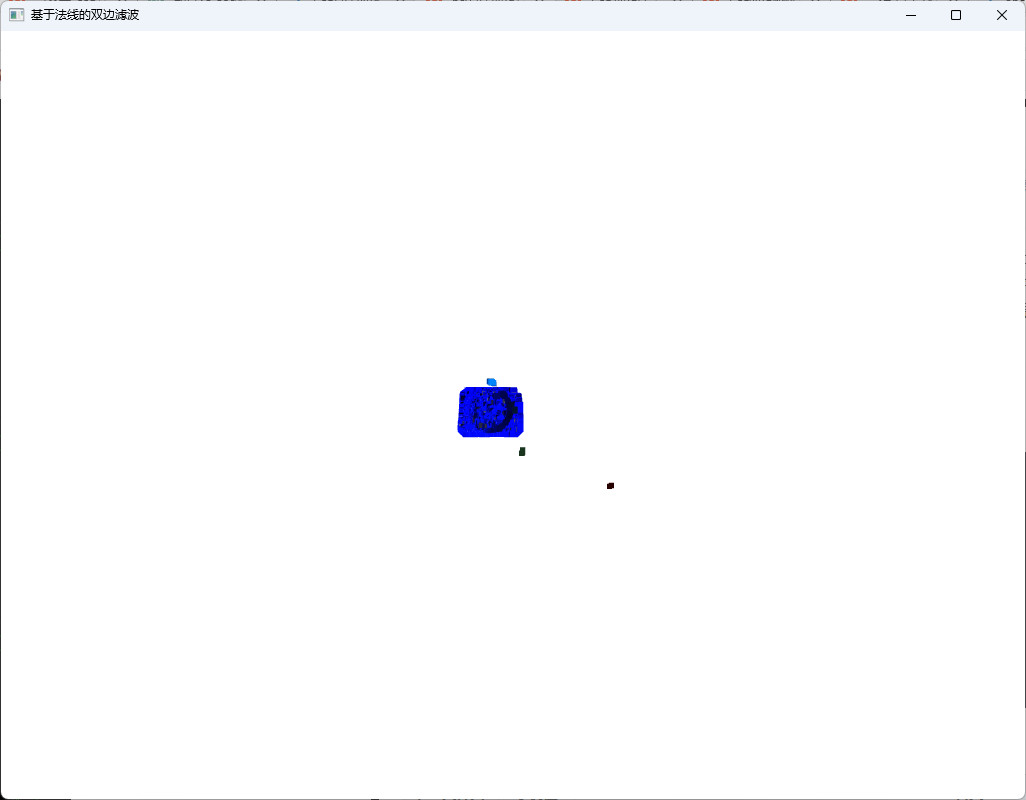
5、运行效果图
运行效果如下所示,供大家参考。直接用python3 astar.py运行即可,