目录
- 引言
- 动机
- 分析
- 主角(Principal Angle)
- 表征子空间距离
- 正交基错配惩罚
- 可迁移表征学习
- 实验
- 数据集介绍
- 实验结果
- 总结与展望
论文链接
相关代码已经开源
引言
深度学习的成功依赖大规模的标记数据,然而人工标注数据的代价巨大。域自适应(Domain Adaptation)意图利用已有源领域标记数据的有效信息学习得到一个可以泛化到目标领域无标记数据上的模型。因此域自适应方法是解决上述问题的方案之一。回归问题作为一个具有广泛应用的机器学习范式,和分类问题具备同等的重要性。然而,当前的研究缺乏一个针对回归问题的深度无监督域自适应方法:(1)已有很多基于实例加权和域不变表征学习的浅层域自适应回归方法,但他们没有办法利用深度网络的表征学习能力,因此不具备处理现实世界多种复杂结构数据的能力。同时,他们往往依赖目标领域中的少量有标数据才能取得理想的性能,即只能做成半监督域自适应方法;(2)已有很多基于深度表征学习的域自适应分类方法,在分类基准数据集上取得了突破性进展,但他们在回归数据集上的表现往往不够理想。因此,本文意在利用深度网络的表征能力,考虑回归问题的本质特点,提出一种适用于回归问题的无监督可迁移域自适应方法。

动机
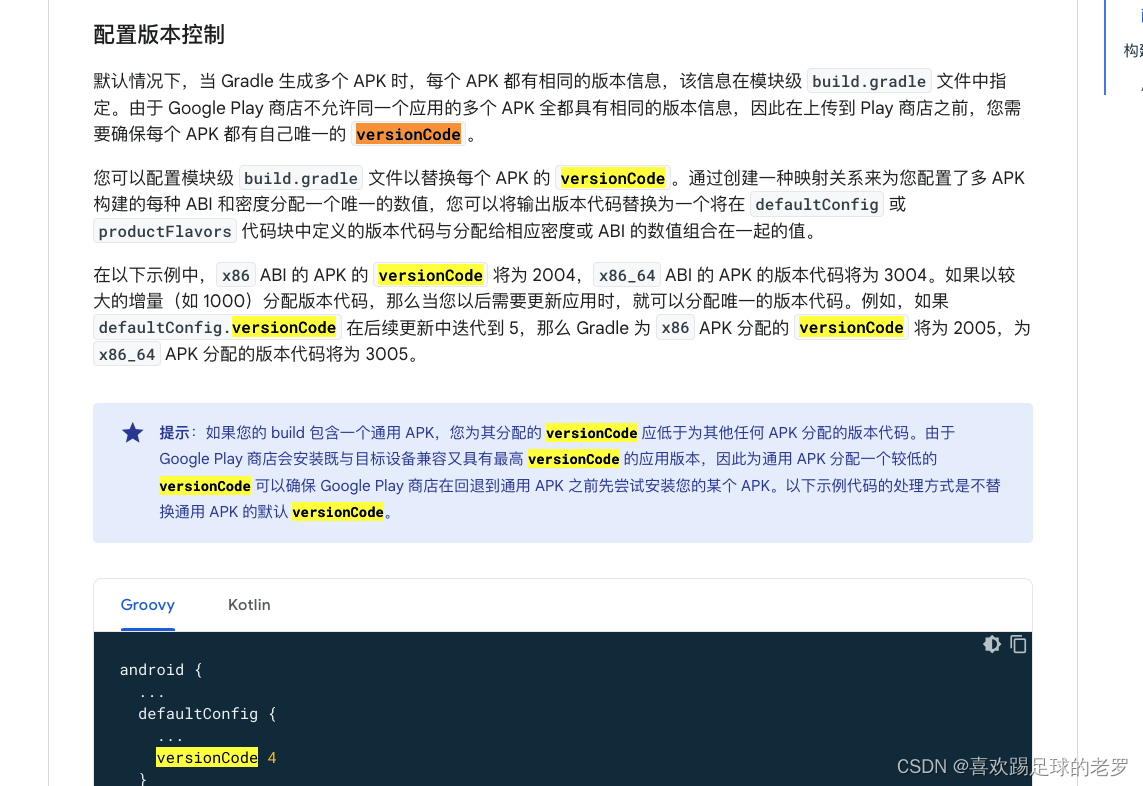
为进一步探索域自适应回归问题,首先要回答的便是深度网络应用在回归问题上和分类问题上是否存在本质差别。为了给出该问题的其中一个答案,我们进行了初步的探索。最直观的一点,便是他们的损失函数有明显差异,分类问题中使用的往往是交叉熵(Cross-Entropy Loss,简称CE)损失函数,而在回归问题中使用的往往是平方差(Squared Loss,简称L2)损失函数。在分类问题中,往往需要将分类器最后一层的输出结果经过Softmax激活函数转化成类别概率,然后才能计算CE。这么做的一个好处就是,对于一个样本,只要分类器输出的激活值的相对大小顺序没有发生明显的变化,最后预测的结果就没有发生变化,因此分类结果理应具备快速适应特征尺度变化的能力。但在回归问题中,只要回归器输出的激活值发生变化,最后预测的结果就一定会发生变化。我们做实验分析了在两类问题中**,性能对特征尺度变化的鲁棒性**。
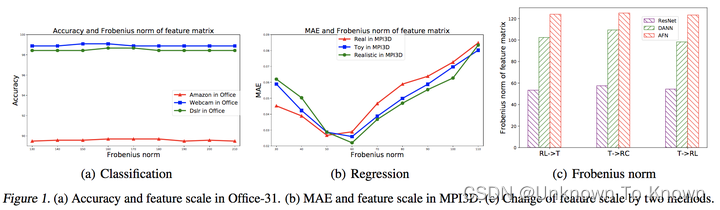
在图(a)中,我们探究了特征尺度变化对分类性能的影响;在图(b)中,我们探究了特征尺度(弗罗贝尼乌斯范数)变化对分类性能的影响;在图(c)中,我们探究了2类常见的域自适应方法对特征尺度的影响。 可以看到,和我们猜想的一样,在分类问题中,特征尺度变化,性能几乎不受影响,但在回归问题中特征尺度变化性能会受到严重的影响。 同时我们在上图中也展示了部分深度域自适应方法,对特征尺度会有明显的影响。 这说明,保持特征尺度不变,是解决域自适应回归问题的根本途径之一!
分析
我们对特征矩阵进行奇异值分解(Singular Value Decomposition)后发现,特征可以分解为正交基和奇异值:
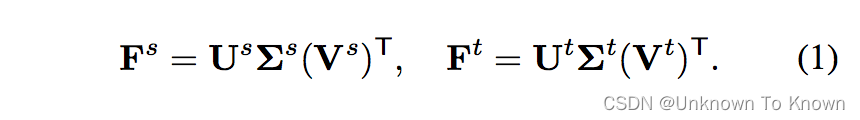
而特征尺度(Frobenius范数)仅仅与奇异值有关系:
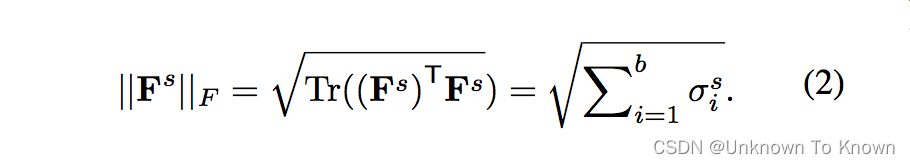
这就说明,如果我们不使用奇异值,而是仅仅使用正交基来拉近领域之间的距离,就有可能不会改变特征尺度!后面,我们会先介绍一种基于正交基的相似度度量方式———主角(Principal Angle),然后针对性的提出一套基于正交基的迁移性表征学习框架。
主角(Principal Angle)
子空间是由一组正交基张成的(一个子空间的正交基可以不同,不同的正交基也可能张成相同的子空间)。 主角(Principal Angle)是子空间相似性度量中一种常见的度量方式。定义如下:

可以看到,第i个主角可以挖掘出两个子空间中夹角第i小的两个正交基,是一种合理的子空间度量方式,也是我们后续距离定义的基础。
表征子空间距离
表征子空间距离(Representation Subspace Distance)是利用主角定义的一种几何距离:

作为子空间中的距离度量,必须满足距离三公理(正定性,对称性,三角不等式):

利用线性代数的相关知识,这三条公理在附录中已经给出了证明,这里不再赘述。
至此,最小化表征子空间距离已经用于学习可迁移表征了,剩下的问题是如何计算主角。 在公式(1)中,我们已经通过对特征矩阵进行SVD得到了正交基:

而主角可以用SVD分解两个子空间的正交基矩阵的矩阵乘积得到:
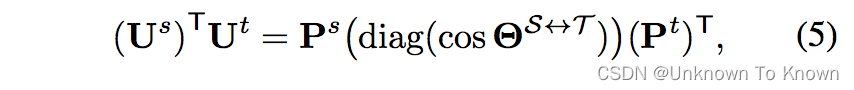
正交基错配惩罚
在主角和表征子空间距离的定义中,我们发现了一个不合理的事实:正交基的匹配和计算,完全是一视同仁的。这是什么意思呢?在获得正交基的过程中:
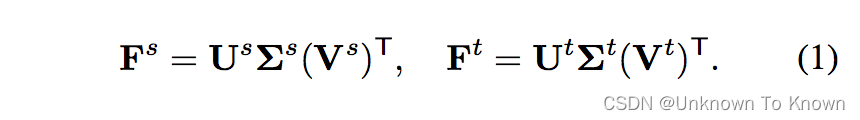
我们可以发现,每个正交基实际上都对应着一个特征值,也就是说,不同正交基实际上是有重要性差别的!显然最大特征值对应的正交基是该子空间中最重要的正交基,而较小特征值对应的正交基则是该子空间中不太重要的正交基,很多时候甚至可以忽略。(如在PCA主成分分析中,这部分不重要的正交基实际上是可以被忽略从而达到降维的目的。)但是,在主角和表征子空间距离的计算中,两个子空间中的正交基只要相似度高,就可以无视其重要性(特征值大小的顺序)被匹配在一起,这显然是不利于达成域自适应的目的的(如迁移了源领域中小特征值的正交基的知识给目标领域中大特征值的正交基,就等同于将源领域的噪声信息传达给了目标领域的主要信息,这显然是有害的)。因此,我们提出了正交基错配惩罚(Basis Mismatch Penalization)来缓解这一问题:
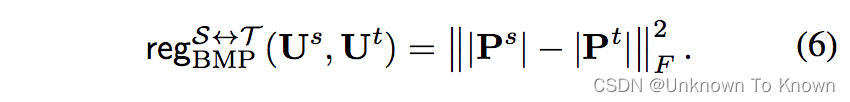
这里的P矩阵即为计算主角的SVD过程中得到的P矩阵:

为什么正交基错配惩罚是这样的形式呢?这需要我们深入理解主角的计算过程:
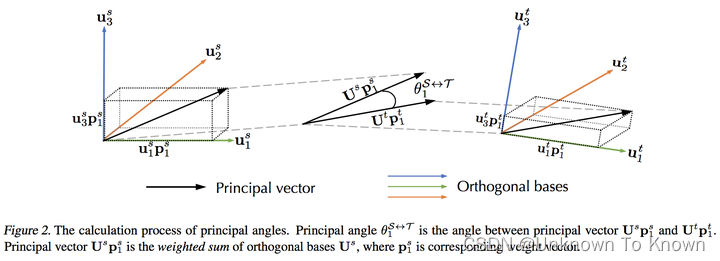
上图是主角的计算过程,传达了2个重要信息: 1.主角是由主向量(Principal Vector)计算余弦相似度匹配得到的。 2.主向量是原特征矩阵正交基的一个加权和,可以将其理解成变换后的新正交基,也就是说主向量和正交基都是张成相同子空间的正交基,只是原特征矩阵正交基是可以明确对应一个特征值的,而主向量则是原正交基做了一个利于计算主角的线性变换得到的。因此,P矩阵实际上存储了每个主向量需要用到的正交基的权重。且实际实验中观察发现,每个主向量往往都被某个正交基支配。如果该权重完全相等,则意味着正交基的匹配完全考虑了特征值大小。 实际中由于领域差异,两个子空间中同样重要的正交基未必具有相同的语义信息,因此完全按照特征值大小匹配也未必合理,利用正交基错配惩罚给一个较小的正则项就可以取得良好的效果。
可迁移表征学习
本文的方法和其他深度域自适应方法相同,即具备有监督学习项和可迁移表征学习项:
(1)在源领域上的有监督学习:
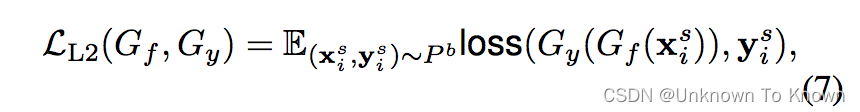
(2)在源领域和目标领域上的可迁移表征学习:
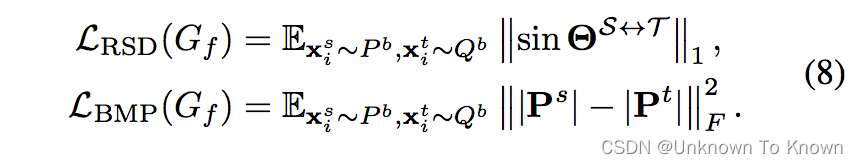
最终组成了一个基于可迁移表征学习的域自适应回归方法:
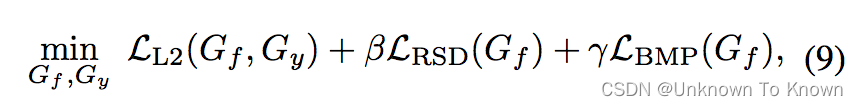
最终的网络架构如下图所示,利用了2阶SVD得到了基于正交基的领域适应方法:
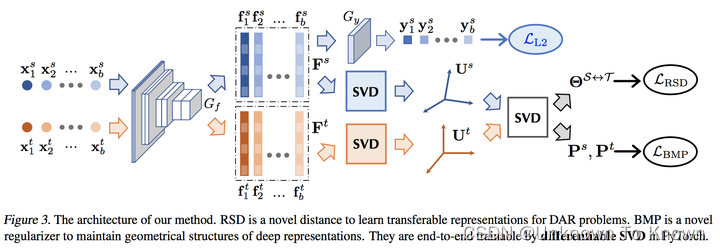
实验
本文利用了已有解耦表征学习领域的2个数据集,首次建立了2个新的域自适应回归基准(Benchmark),他们分别是2D的合成形状图像数据集dSprites和3D的虚拟现实数据集MPI3D。同时,我们也在现实的人体头部姿势估计数据集Biwi Kinect上验证了我们方法的有效性。
数据集介绍
dSprites中有4个回归任务和1个分类任务,如下表所示,但由于方向(Orientation)任务无法完全解耦(不同形状的物体,旋转角度的周期性不同),所以我们在此数据集中的回归任务为物体大小(Scale)和位置的横纵坐标(Position X, Position Y)。相关的图像示例如下图所示,由于共有3个领域,所以共可构建6个迁移任务。


MPI3D中有5个分类任务和2个回归任务,如下表所示,我们在此数据集中的回归任务也即为该数据集全部的回归任务(Horizontal Axis, Vertical Axis)。相关的图像示例如下图所示,由于共有3个领域,所以共可构建6个迁移任务。
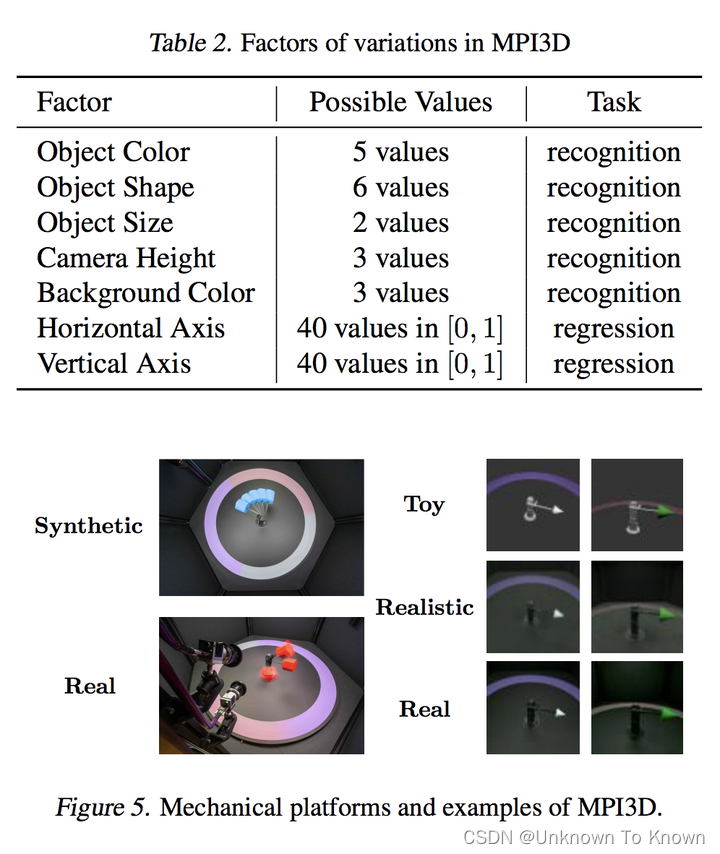
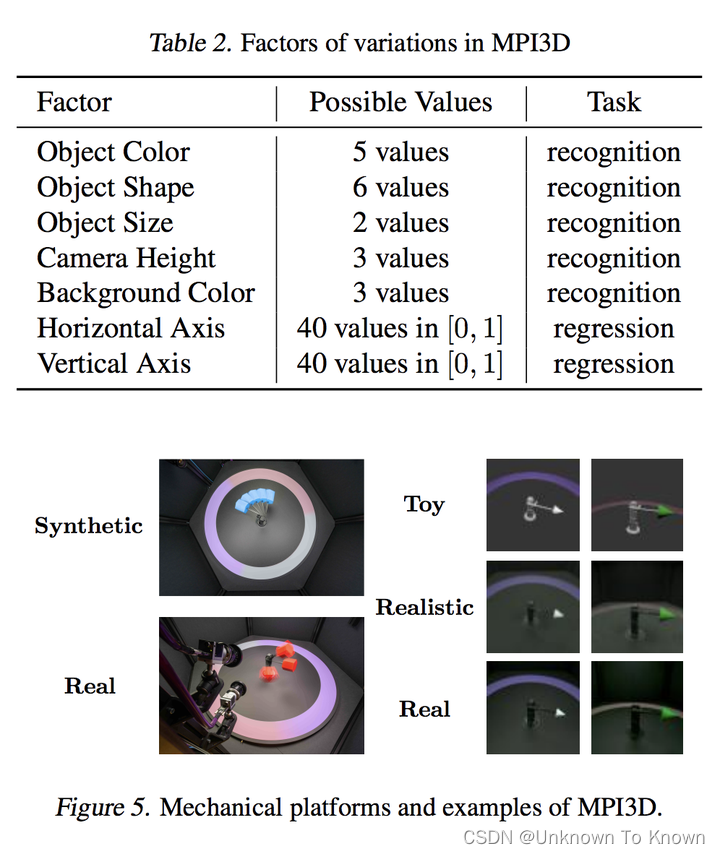
Biwi Kinect中有3个回归任务,如下表所示,我们在此数据集中的回归任务也即为该数据集全部的回归任务(Pitch, Yaw and Roll)。相关的图像示例如下图所示,我们人为将其分为男性和女性两个领域,因此共有2个迁移任务。

实验结果

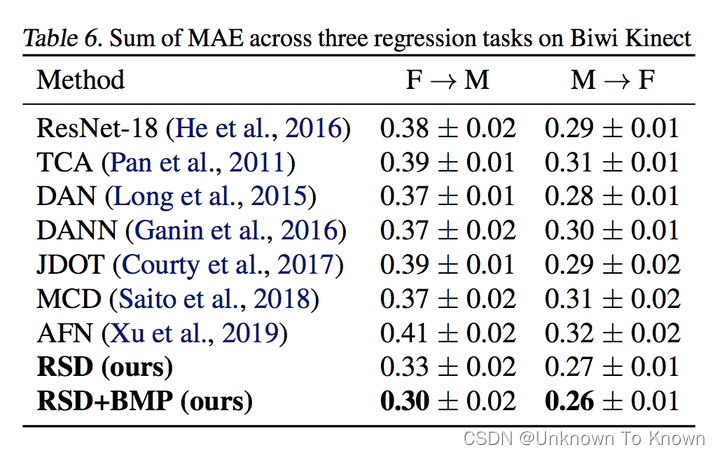
可以看出,我们的方法在各数据集上均有明显的提升,而部分深度域自适应分类方法也可以用在回归任务上且取得一定的性能提升。
总结与展望
本文对深度域自适应回归方法进行了初步探索,基于深度回归里存在的本质问题:输出对特征尺度的变化极为敏感这一特点,提出了基于正交基的可迁移表征学习方法。本文作为对深度域自适应回归问题的初步探索,希望能对后续的域自适应回归工作提供思路。




![[架构之路-238]:目标系统 - 纵向分层 - 网络通信 - 网络规划与设计框架](https://img-blog.csdnimg.cn/40fd6973ef404b59bd5fb31bc3ece5e8.png)