一. 堆

1. 堆的概念

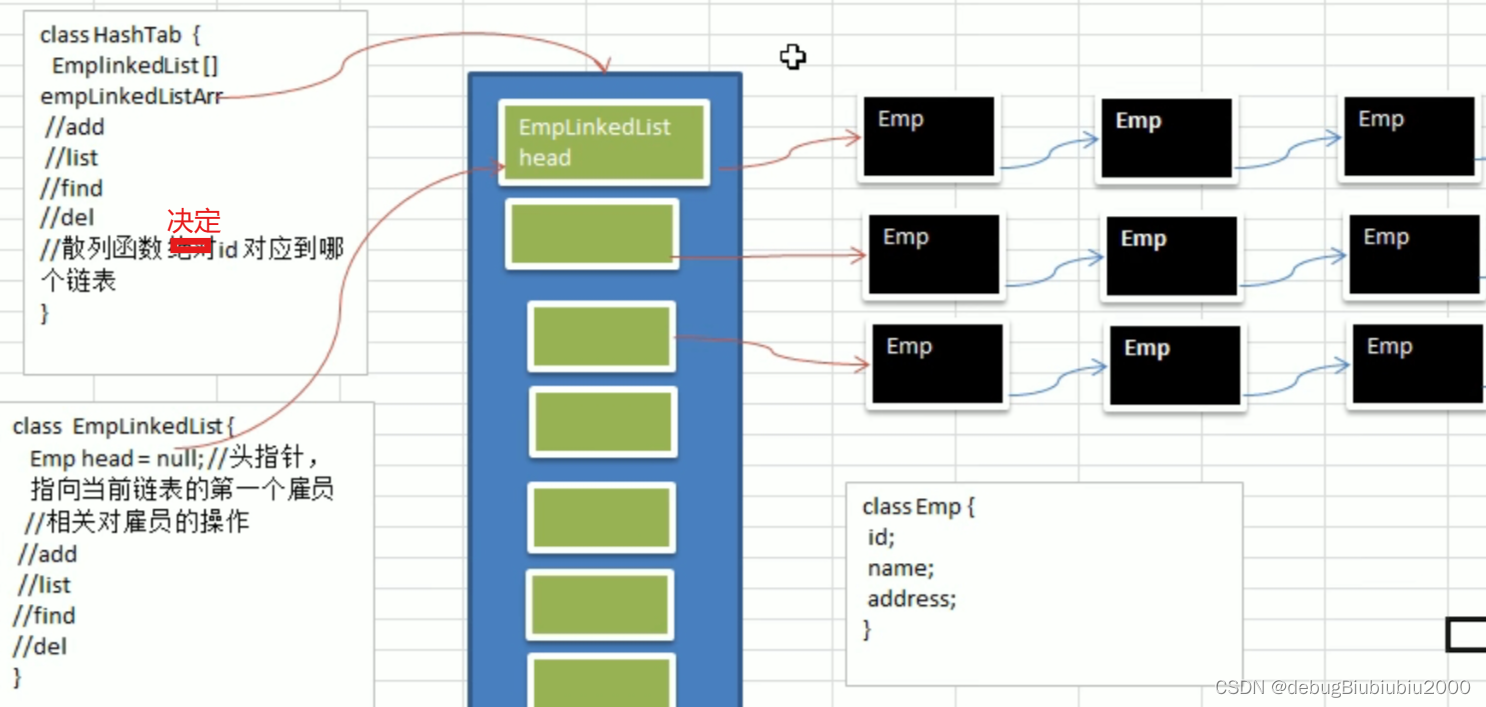
堆（heap）：一种有特殊用途的数据结构——用来在一组变化频繁（发生增删查改的频率较高）的数据集中查找最值。
堆在物理层面上，表现为一组连续的数组区间：long[] array ；将整个数组看作是堆。
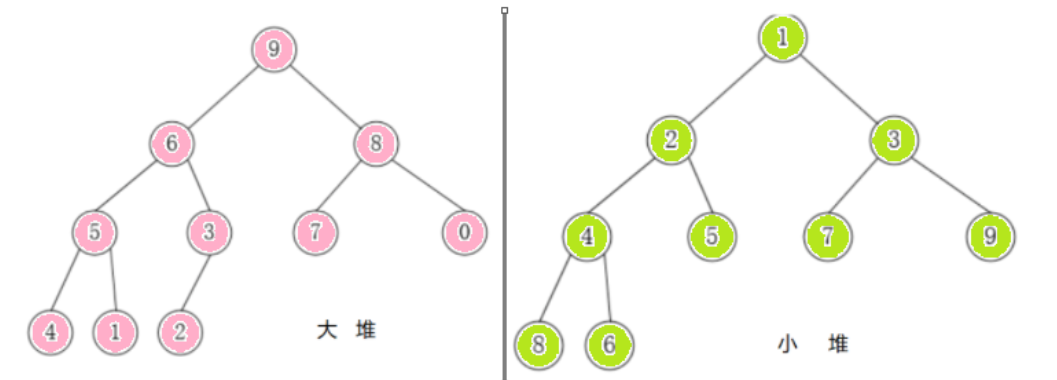
堆在逻辑结构上，一般被视为是一颗完全二叉树。
满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆；反之，则是小堆，或者小根堆，或者最小堆。当一个堆为大堆时，它的每一棵子树都是大堆。

2. 堆的存储方式

从堆的概念可知，堆是一棵完全二叉树，因此可以层序的规则采用顺序的方式来高效存储；
假设 i 为结点在数组中的下标，则有：

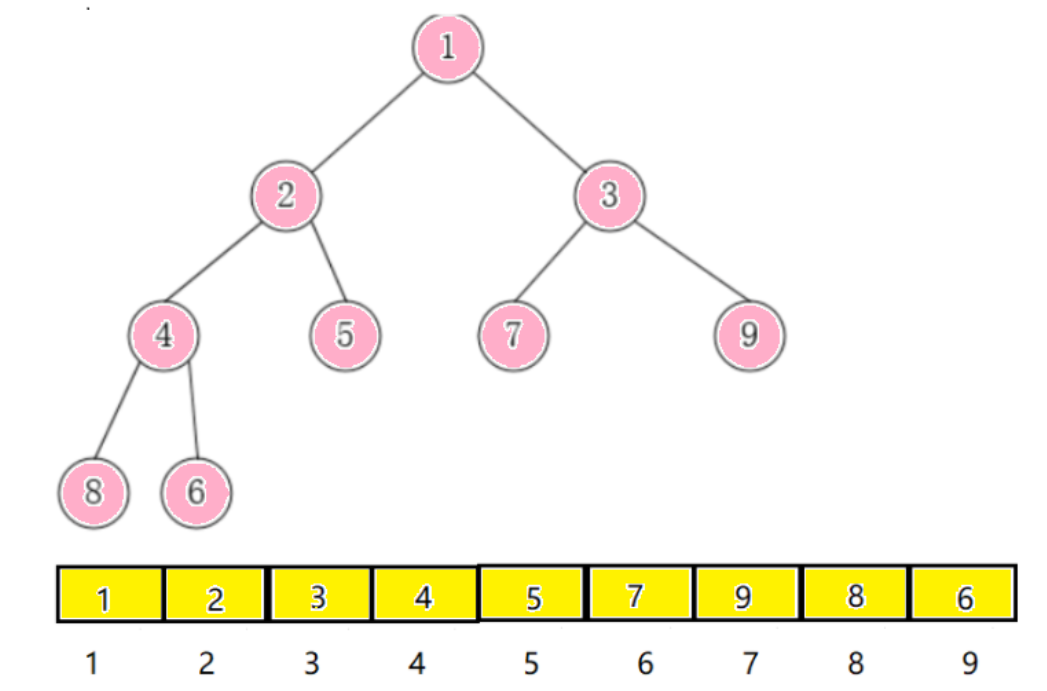
如果 i 为 0，则 i 表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2；
如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子；
如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子。

二. 堆的基本操作

1. 创建堆，向下调整与向上调整

创建堆只有两种堆可以创建，要不就是大根堆，要不就是小根堆。而要满足大根堆还是小根堆的逻辑，就要向下调整的操作才能实现。要想自己实现堆，堆本身就是一个数组，因此创建一个数组来创建堆。
对于集合 { 27,15,19,18,28,34,65,49,25,37 } 中的数据，如果将其创建成堆呢？

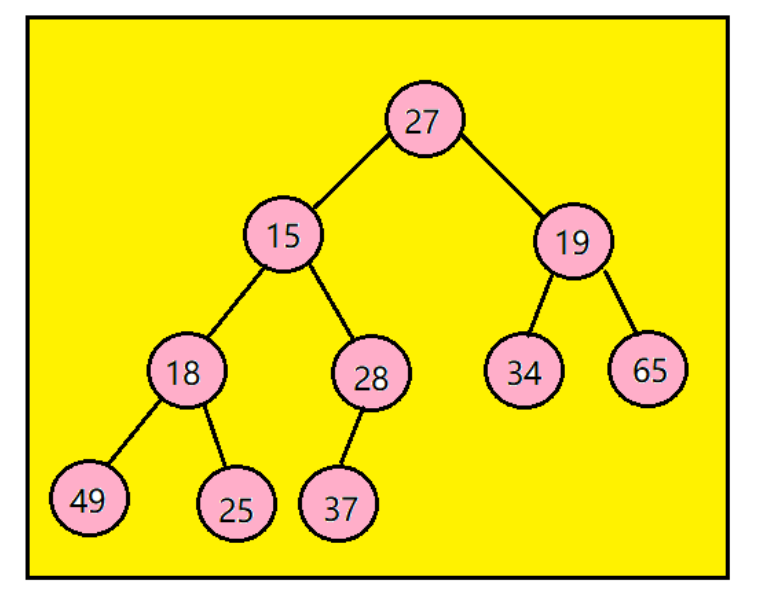
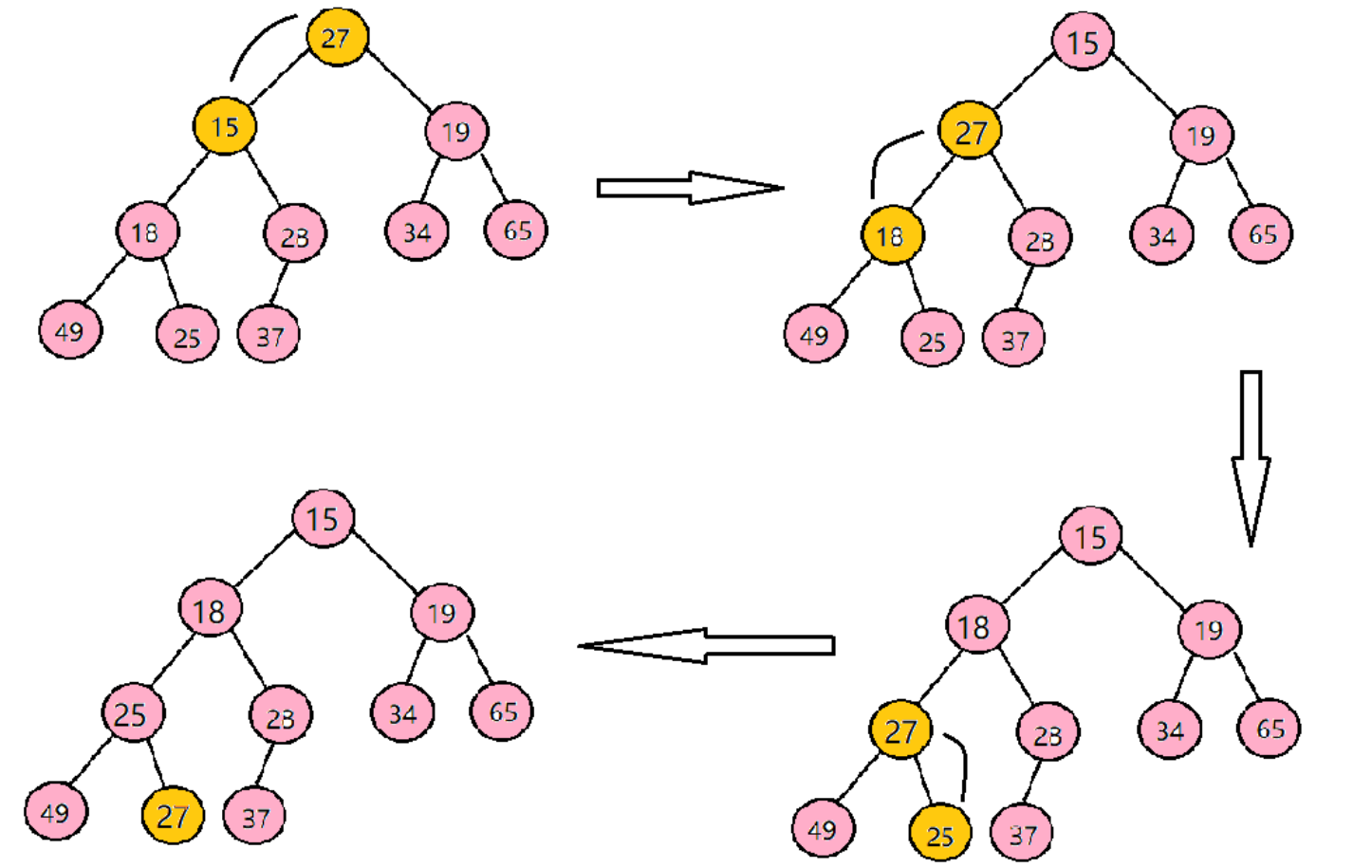
仔细观察上图后发现：根节点的左右子树已经完全满足堆的性质，因此只需将根节点向下调整好即可。 向下过程(以小堆为例)：

1. 让 parent 标记需要调整的节点，child 标记 parent 的左孩子(注意：parent 如果有孩子一定先是有左 孩子)
2. 如果 parent 的左孩子存在，即: child < size， 进行以下操作，直到 parent 的左孩子不存在：
   • 看 parent 右孩子是否存在，存在找到左右孩子中最小的孩子，让 child 进行标
   • 将 parent 与较小的孩子 child 比较，如果：
   • parent 小于较小的孩子 child，调整结束；
   • 否则：交换 parent 与较小的孩子 child，交换完成之后，parent 中大的元素向下移动，可能导致子树不满足对的性质，因此需要 继续向下调整，即 parent = child;child = parent*2+1;然后继续 2

def sift(li, low, high):
    """
    建立大根堆
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """
    i = low  # 最开始指向根节点
    j = 2 * i + 1  # 开始是左孩子
    tmp = li[low]  # 把堆顶存起来
    # 只要j位置有数
    while j <= high:
        # 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子大
        if j + 1 <= high and li[j + 1] > li[j]:
            j = j + 1  # 把j指向右孩子
        # 比较堆顶的tmp和j左右孩子大小比较
        if li[j] > tmp:  # 如果孩子比堆顶大
            li[i] = li[j]  # 把孩子大的换到上面父节点
            # 往下看一层，将i移动到孩子位置，将j继续向下移动到新i的孩子的位置
            i = j
            j = 2 * i + 1
        else:  # tmp更大，把tmp放到i的位置上 结束循环
            li[i] = tmp  # 把tmp放到某一级领导位置上
            break
    # 越界了
    else:
        li[i] = tmp  # 说明i走到最下面一层了，j到还要下一层没有叶子节点位置，是空的，就把tmp放到叶子节点上

def sift(li, low, high):
    """
    建立小根堆
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """

    i = low  # 最开始指向根节点
    j = 2 * i + 1  # 开始是左孩子
    tmp = li[low]  # 把堆顶存起来
    # 只要j位置有数
    while j <= high:
        # 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子小
        if j + 1 <= high and li[j + 1] < li[j]:
            j = j + 1  # 把j指向右孩子
        # 比较堆顶的tmp和j左右孩子大小比较
        if li[j] < tmp:  # 如果孩子比堆顶小
            li[i] = li[j]  # 把孩子大的换到上面父节点
            # 往下看一层，将i移动到孩子位置，将j继续向下移动到新i的孩子的位置
            i = j
            j = 2 * i + 1
        else:  # tmp更大，把tmp放到i的位置上 结束循环
            li[i] = tmp  # 把tmp放到某一级领导位置上
            break
    # 越界了
    else:
        li[i] = tmp  # 说明i走到最下面一层了，j到还要下一层没有叶子节点位置，是空的，就把tmp放到叶子节点上

建堆的时间复杂度是 O(n) ；向下调整的时间复杂度是 O(log(n))。

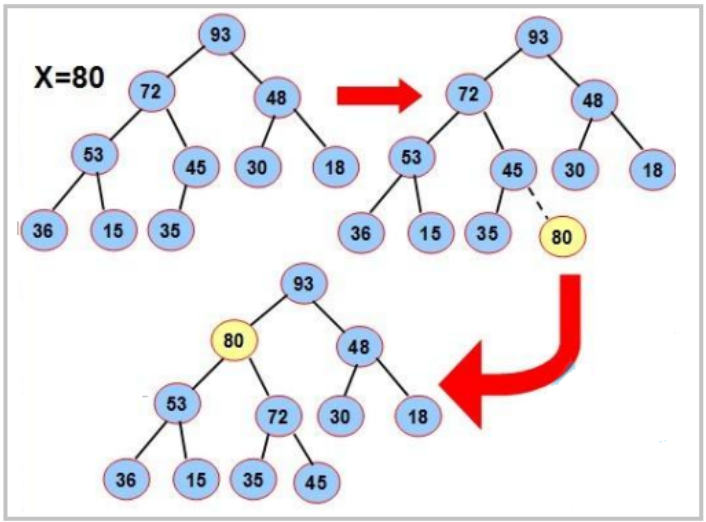
2. 堆的插入(offer）

堆的插入总共需要两个步骤：

1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
2. 将最后新插入的节点向上调整，直到满足堆的性质 ；

3. 堆的删除(poll)

具体如下：（ 注意：堆的删除一定删除的是堆顶元素。）

1. 将堆顶元素对堆中最后一个元素交换；
2. 将堆中有效数据个数减少一个；
3. 对堆顶元素进行向下调整；
   代码待补充…

三. 堆的应用

1. 堆排序（从小到大排）

一个数组根据从小到大排序，要创建大堆来排；一个数组根据从大到小排序，要创建小堆来排。
此处就以创建大堆为例。首先将堆顶的元素和堆中的最后一个元素交换，交换后再向下调整，调整后再与堆的倒数第二个元素进行交换。

def sift(li, low, high):
    """
    向下调整的一次过程
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """

    i = low  # 最开始指向根节点
    j = 2 * i + 1  # 开始是左孩子
    tmp = li[low]  # 把堆顶存起来
    # 只要j位置有数
    while j <= high:
        # 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子大
        if j + 1 <= high and li[j + 1] > li[j]:
            j = j + 1  # 把j指向右孩子
        # 比较堆顶的tmp和j左右孩子大小比较
        if li[j] > tmp:  # 如果孩子比堆顶大
            li[i] = li[j]  # 把孩子大的换到上面父节点
            # 往下看一层，将i移动到孩子位置，将j继续向下移动到新i的孩子的位置
            i = j
            j = 2 * i + 1
        else:  # tmp更大，把tmp放到i的位置上 结束循环
            li[i] = tmp  # 把tmp放到某一级领导位置上
            break
    # 越界了
    else:
        li[i] = tmp  # 说明i走到最下面一层了，j到还要下一层没有叶子节点位置，是空的，就把tmp放到叶子节点上


# 堆排序过程
def heap_sort(li):
    """
    1. 先建堆  从最后一个子堆开始，小堆到大堆 依次到根节点
    2. 向下调整 得到堆顶元素，为最大元素
    3. 挨个出数 堆顶最大元素和堆最后一个元素交换位置
    4. 重复2-3，直到堆变空
    :param li:待排序的列表
    :return:
    """
    print("开始建大根堆")
    # n 列表长度
    n = len(li)
    # 遍历范围 首先求列表最后一个父元素，最后一个小堆，最后一个子元素下标是n - 1，父下标((n-1)-1))//2,通过左右孩子公式都一样的结果
    # 最后一个父元素开始，最后-1步长是倒着遍历到列表最后一个元素 找到堆顶0(中间-1，步长负数，-1+1=0)，倒序遍历
    for i in range((n - 2) // 2, -1, -1):
        sift(li, i, n - 1)
    # for循环结束，建堆完成了

    # 挨个出数
    for i in range(n - 1, -1, -1):  # 倒序 i从最后开始
        # i指向当前堆的最后一个元素
        li[0], li[i] = li[i], li[0]
        # 由于是倒序，挨个出数后，尾部有序区指针high，每次左移一位
        sift(li, 0, i - 1)  # i-1是新的high

li = [9, 6, 3, 5, 7, 2, 1, 8, 4]

print(li)
heap_sort(li)
print(li)

2. top-k问题

若要从N个数字中取得最小的K个数字，则需要创建大小为K的大堆来获取。若要从N个数字中取得最大的K个数字，则需要创建大小为K的小堆来获取。

def sift(li, low, high):
    """
    向上调整的一次过程
    :param li: 列表
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """

    i = low  # 最开始指向根节点
    j = 2 * i + 1  # 开始是左孩子
    tmp = li[low]  # 把堆顶存起来
    # 只要j位置有数
    while j <= high:
        # 左孩子和右孩子比较大小 右孩子有没有越界 且 右孩子比左孩子小
        if j + 1 <= high and li[j + 1] < li[j]:
            j = j + 1  # 把j指向右孩子
        # 比较堆顶的tmp和j左右孩子大小比较
        if li[j] < tmp:  # 如果孩子比堆顶小
            li[i] = li[j]  # 把孩子大的换到上面父节点
            # 往下看一层，将i移动到孩子位置，将j继续向下移动到新i的孩子的位置
            i = j
            j = 2 * i + 1
        else:  # tmp更大，把tmp放到i的位置上 结束循环
            li[i] = tmp  # 把tmp放到某一级领导位置上
            break
    # 越界了
    else:
        li[i] = tmp  # 说明i走到最下面一层了，j到还要下一层没有叶子节点位置，是空的，就把tmp放到叶子节点上

def topk(li, k):
    # 先取列表前k个元素
    heap = li[0:k]
    # 1. 建小根堆
    for i in range((k - 2) // 2, -1, -1):
        sift(heap, i, k - 1)

    print("*" * 80)
    print("小根堆heap建堆完成，", heap)
    print("*" * 80)

    # 2. 遍历 li列表里k后面剩下的元素
    for i in range(k, len(li)):
        # 依次拿k后面的值和小根堆 堆顶的值比较大小
        if li[i] > heap[0]:  # 如果值 大于 堆顶元素值
            heap[0] = li[i]  # 把大的值 放到堆顶
            sift(heap, 0, k - 1)
    # 3. 挨个出数
    for i in range(k - 1, -1, -1):  # 倒序 i从最后开始
        # i指向当前堆的最后一个元素
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i - 1)  # i-1是新的high
    return heap

li = [i for i in range(20)]
random.shuffle(li)

print(li)
print(topk(li, 10))
print(li)