目录

一、回溯算法基础

回溯法模板

二、（leetcode 77）组合

剪枝 

---

一、回溯算法基础

1.回溯的本质是穷举，穷举所有可能，然后选出想要的答案（为了提升效率，最多再加一个剪枝）

2.回溯法解决的问题都可以抽象为树形结构

因为回溯法解决的都是在集合中递归查找子集

• 集合的大小就构成了树的宽度，递归的深度，都构成的树的深度
• 递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）

回溯法模板

• 回溯函数模板返回值以及参数（参数不是一开始就能确定的）
• 回溯函数终止条件
• 回溯搜索的遍历过程

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

二、（leetcode 77）组合

力扣题目链接

暴力算法不可取，毕竟如果k=50,就要循环50次

回溯法就用递归来解决嵌套层数的问题

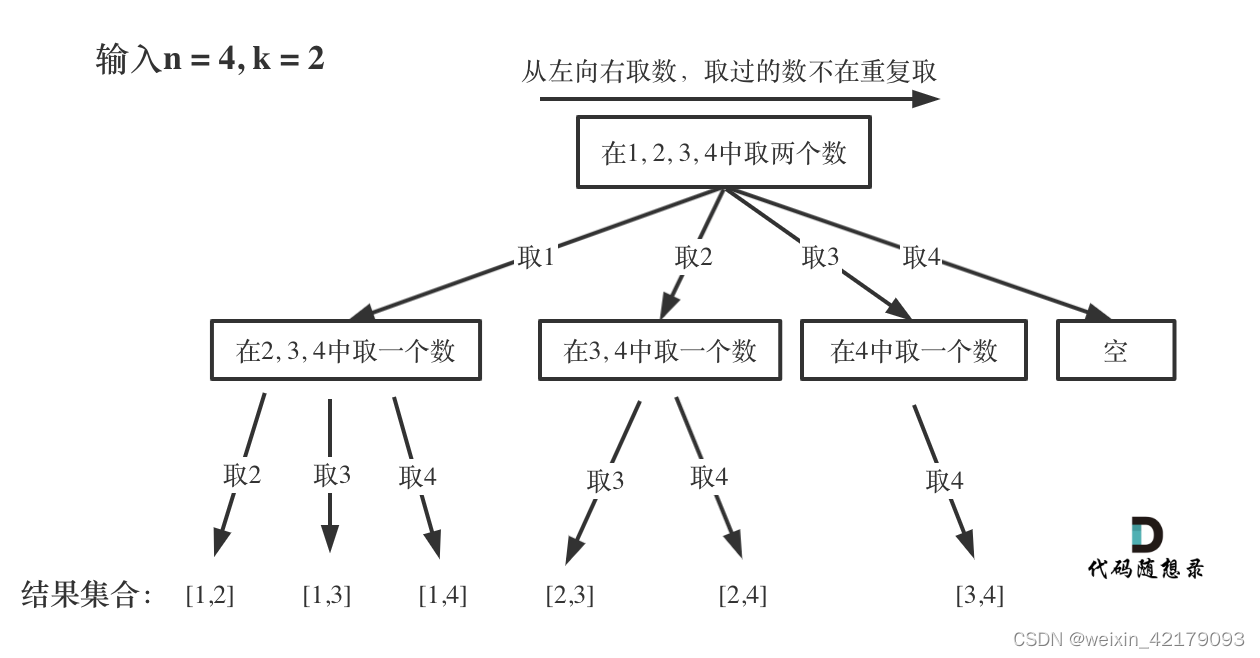
class Solution {
private:
    vector<vector<int>> result; 
    vector<int> path; // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1); // 递归
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

剪枝 

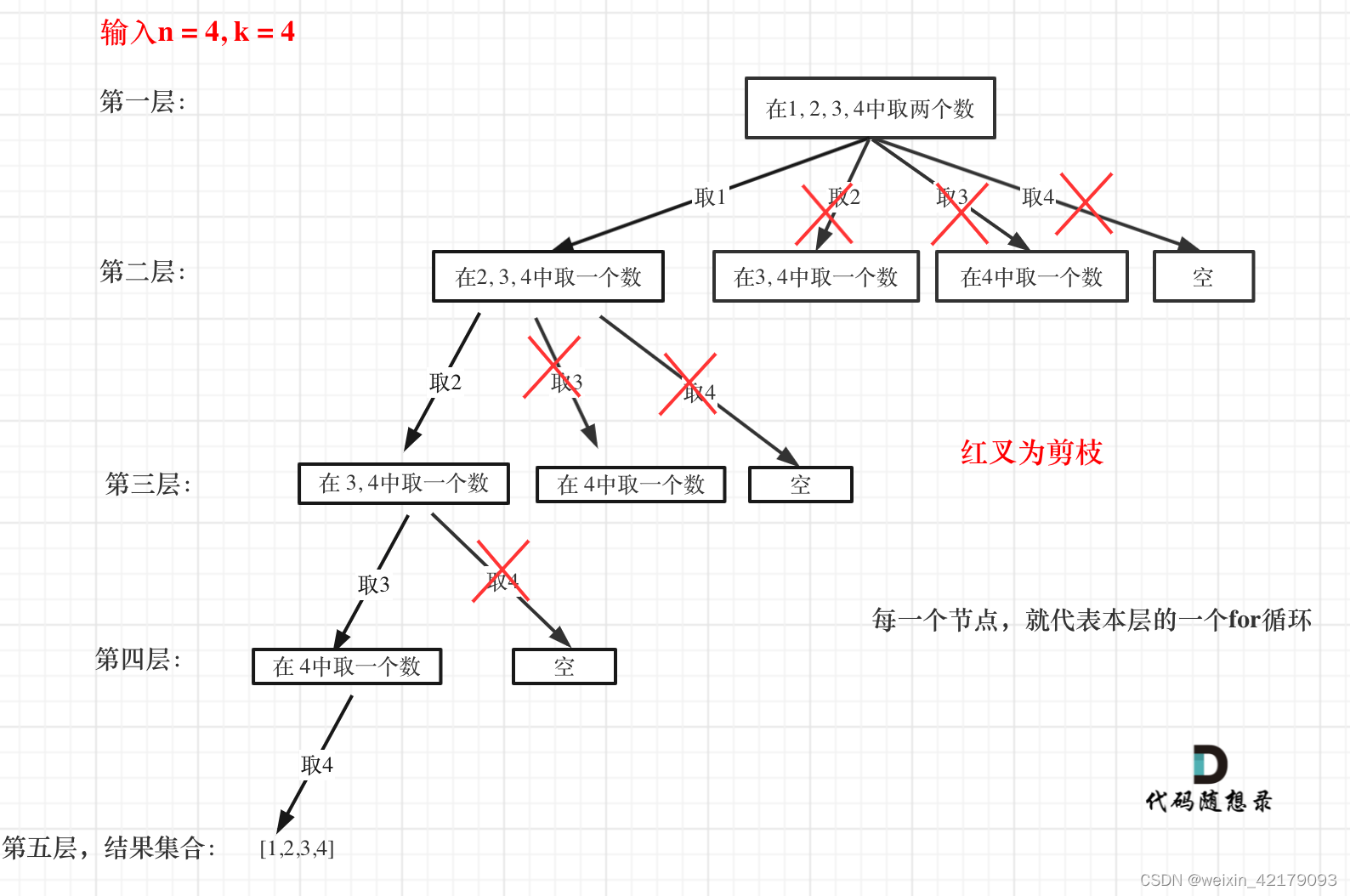
优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置