介绍：

  哈夫曼树（Huffman Tree）是一种用于数据压缩的树形数据结构。它是由刚特·哈夫曼于1952年发明的。

  哈夫曼树的特点是：对于一个长度为n的字符集，它可以将每个字符在树上表示为一个唯一的二进制编码。在哈夫曼树中，每个叶节点都代表一个字符，并且每个叶节点的权值都等于该字符在原始字符集中的出现频率。哈夫曼树的构建算法保证了权值越高的节点越靠近根节点，使得出现频率高的字符拥有最短的编码，从而达到数据压缩的效果。

构建哈夫曼树的步骤：

1. 根据字符出现频率，将所有字符按权值从小到大排序。

2. 选出权值最小的两个字符作为左右子树，创建一个新的节点，将这两个节点作为新节点的子节点，并将新节点的权值设为这两个节点的权值之和。

3. 将新节点插入到原来的字符集中，并重新排序。

4. 重复步骤2和步骤3，直到只剩下一个节点，即为哈夫曼树的根节点。

从哈夫曼树的根节点开始到每个叶节点的路径就是该叶节点对应字符的哈夫曼编码。通过哈夫曼编码，可以将原始字符串中的字符转换为二进制编码，从而实现数据压缩。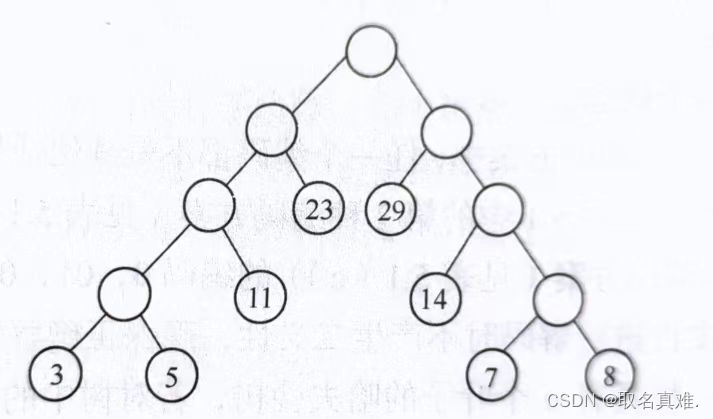

简单哈夫曼树建立：

输入：节点个数，以及各点权值

思路：代码注释里

输出：各点的权值，双亲，左右孩子

代码：

#include<iostream>//建立哈夫曼树
using namespace std;
typedef struct node
{
	int weight;
	int parent, lchid, rchild;

}HT,*Htree;
int flag[1000] = { 0 };
void Select(Htree& ht, int n, int& s1, int& s2)
{
	int min1=999, min2=999;
	for (int i = 1; i <= n; i++)//查找权值第一小的点
	{
		if (flag[i] == 0 && (ht[i].weight < min1))
		{
			min1 = ht[i].weight;
			s1 = i;
		}
	}
	flag[s1] = 1;//标记该点移出
	for (int i = 1; i <= n; i++)//查找权值第二小的点
	{
		if (flag[i] == 0 && (ht[i].weight < min2))
		{
			min2 = ht[i].weight;
			s2 = i;
		}
	}
	flag[s2] = 1;//标记该点移出
}
void Inithtree(Htree& ht, int n)//初始化
{
	if (n <= 1) return;
	int m = 2 * n - 1;
	ht = new HT[m+1];
	for (int i = 1; i <= m; i++)//将1到m点中的父亲、左孩子、右孩子下标都初始为0
		ht[i].parent = 0, ht[i].lchid = 0, ht[i].rchild = 0;
	cout << "输入各点权值:" << endl;
	for (int i = 1; i <= n; i++)
		cin >> ht[i].weight;
}
void Createhtree(Htree& ht, int n)//建树
{
	int s1, s2;
	for (int i = n + 1; i <= 2 * n - 1; i++)//循环n-1次，建树
	{
		Select(ht, i - 1, s1, s2);//查找两个父亲为0且权值最小的点，并返回序号s1、s2
		ht[s1].parent = i, ht[s2].parent = i;//s1、s2父亲改为i
		ht[i].lchid = s1, ht[i].rchild = s2;//s1、s2分别作为i的左右孩子
		ht[i].weight = ht[s1].weight + ht[s2].weight;//i的权值为左右孩子权值之和
	}
}
void Printtree(Htree& ht, int n)
{
	for (int i = 1; i <= 2 * n - 1; i++)
		cout << i <<" "<< ht[i].weight << " " << ht[i].parent << " " << ht[i].lchid << " " << ht[i].rchild << endl;
}
int main()
{
	Htree h;
	int n;
	cin >> n;//输入节点个数
	Inithtree(h,n);
	Createhtree(h, n);
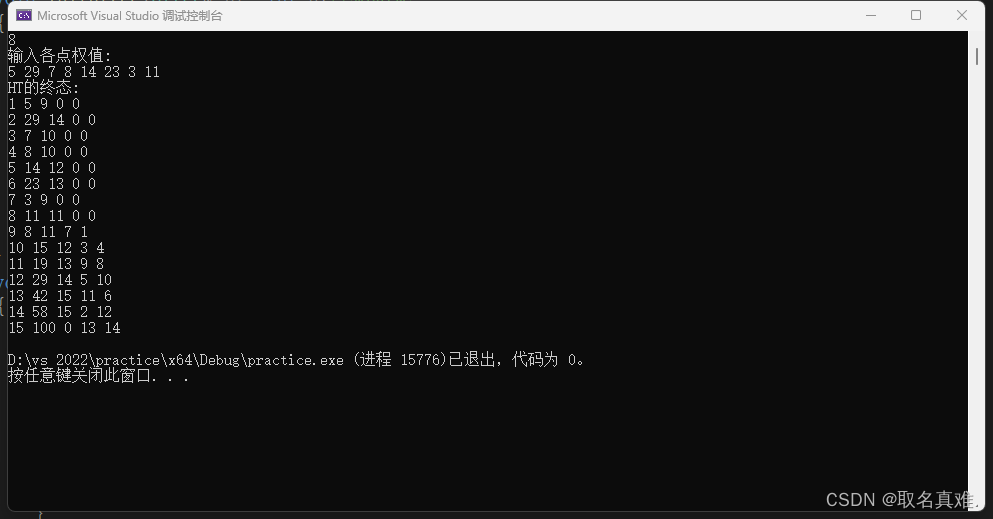
	cout << "HT的终态:" << endl;
	Printtree(h, n);
}