OpenCV Python KMeans 的理解
【目标】
- 理解KMeans聚类的基础概念
- KMeans是如何工作的,
【理论】
Tshirt尺寸问题
有个公司,打算投放一批T-shirt到市场上售卖,但是不知道人们需要什么样的尺寸,而且工厂也不会制作所有的尺寸样衣,所以,他们需要想办法,用尽可能少的尺寸数量满足用户需求。
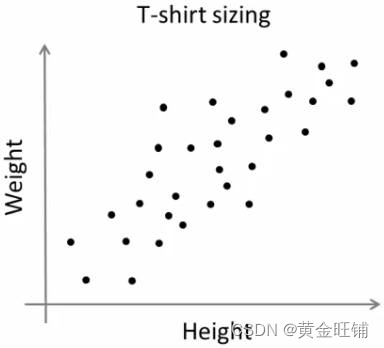
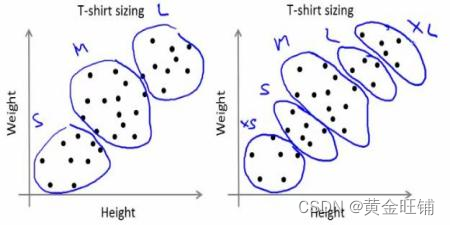
他们把人分为小、中、大三种,只生产这三种适合所有人的型号。这种将人分成三组的方法可以通过k-means聚类来实现,算法提供了满足所有人的最佳3个大小。如果没有,公司可以把人们分成更多的小组,可能是五组,以此类推。请看下图:
K-Means步骤
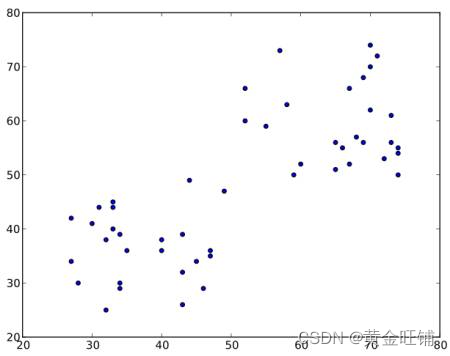
该算法就是一个迭代更新的过程,下面将一步一步的进行介绍。以下图数据为例(可以认定为T-shirt问题,下图的数据,我们将它们聚为2类):
1. 随机选择聚类中心 C 1 C1 C1 和 C 2 C2 C2
2. 计算距离并标记
分别计算每个点到两个质心的距离,看与哪个质心更近,如果与
C
1
C1
C1 近,则认为属于类别0 , 与
C
2
C2
C2 近,认为属于类别 1。 (此处 0,1 为 设定的类别号),本例中0表示红色,1表示蓝色;
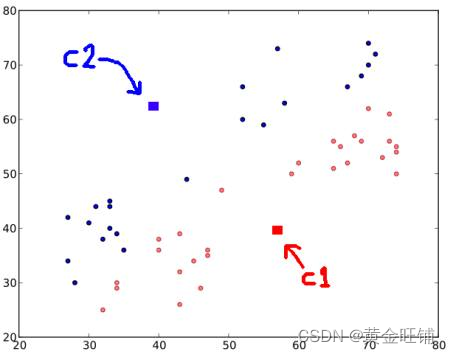
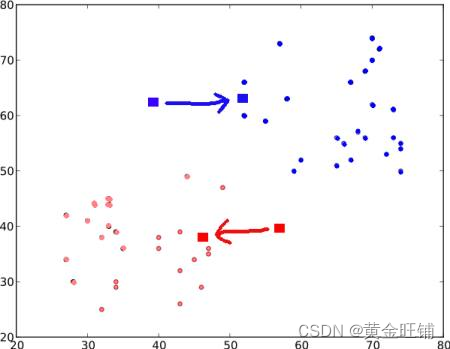
3. 重新计算分配
分别计算所有红色点和蓝色点的平均值,新的平均值就是新的质心,也是新的 C 1 C1 C1 和 C 2 C2 C2
不停的进行步骤2 和步骤 3, 得到下图的结果。
迭代进行以上步骤后,直到两个质心都收敛到固定点(或者收敛到我们设定的值,例如最大迭代次数,达到的精度等)。简单的说,就是 C 1 ↔ R e d P o i n t s C1↔RedPoints C1↔RedPoints 与 C 2 ↔ B l u e P o i n t s C2↔BluePoints C2↔BluePoints 距离和最小。
m i n i m i z e [ J = ∑ A l l R e d P o i n t s d i s t a n c e ( C 1 , R e d P o i n t ) + ∑ A l l B l u e P o i n t s d i s t a n c e ( C 2 , B l u e P o i n t ) ] minimize \lbrack J=\sum_{AllRedPoints}{distance(C1,RedPoint)} + \sum_{AllBluePoints}{distance(C2,BluePoint)} \rbrack minimize[J=AllRedPoints∑distance(C1,RedPoint)+AllBluePoints∑distance(C2,BluePoint)]
最终的效果如下:
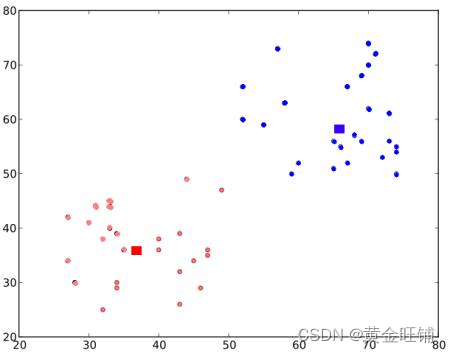
这只是对KMeans的直观理解,若要理解更多的细节,请看专业的机器学习书籍。
【参考】
- Understanding K-Means Clustering
- Machine Learning Course, Video lectures by Prof. Andrew Ng (Some of the images are taken from this)