文章目录
- abstract
- 圆的参数方程
- 匀速圆周运动的轨迹
- 从普通方程直接转化为参数方程
- 任意位置圆心的方程
- 参数方程
- 一般方程
- 例
- 交点问题的参数方程法
- 圆锥曲线的参数方程
- 椭圆参数方程
- 例
- 椭圆内接矩形的最大面积问题
- 抛物线参数方程
- 一般位置的抛物线
- 例
- 双曲线的参数方程
- 点到双曲线的最短距离
- 例
abstract
- 圆和圆锥曲线的参数方程
圆的参数方程
匀速圆周运动的轨迹
- 圆可以看作是质点作匀速圆周运动下的轨道曲线
- 质点以匀角速度
ω
\omega
ω作圆周运动,圆心在原点,半径为
R
R
R
- 下面建立运动的轨迹方程.
- 记
t
t
t为时间,运动开始时
t
=
0
t=0
t=0,质点位于点
A
A
A处,
- 在时刻 t t t,质点位于点 M ( x , y ) M(x,y) M(x,y)处.
- 由物理学知识, θ = ω t \theta=\omega{t} θ=ωt, θ \theta θ为 O x Ox Ox轴正向到向径 O M → \overrightarrow{OM} OM所成的角,
- 因此得参数方程组
(1):- x = R cos ω t x=R\cos\omega{t} x=Rcosωt; y = R sin ω t y=R\sin\omega{t} y=Rsinωt; t ⩾ 0 t\geqslant{0} t⩾0
- 这是圆周运动的轨迹方程,参数为 t t t
- 也可以以
θ
=
ω
t
\theta=\omega{t}
θ=ωt作为参数(此时参数具有明显的意义),方程
(2):- x = R cos θ x=R\cos\theta x=Rcosθ; y = R sin θ y=R\sin\theta y=Rsinθ; θ ∈ [ 0 , 2 π ] \theta\in[0,2\pi] θ∈[0,2π]
从普通方程直接转化为参数方程
- 主要应用毕达哥拉斯三角恒定关系: sin 2 θ + cos 2 θ = 1 \sin^2{\theta}+\cos^2\theta=1 sin2θ+cos2θ=1实现转换
- 方程(2)可以由圆的普通方程转化得出
- x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2;即 ( x R ) 2 + ( y R ) 2 (\frac{x}{R})^2+(\frac{y}{R})^2 (Rx)2+(Ry)2= 1 1 1
- 令 x R = cos θ \frac{x}{R}=\cos\theta Rx=cosθ; y R = sin θ \frac{y}{R}=\sin\theta Ry=sinθ,则得到方程(2)
- 这个方法对于其他的一些二次曲线也有效,例如圆锥曲线
任意位置圆心的方程
- 若圆心在点
M
(
x
0
,
y
0
)
M(x_0,y_0)
M(x0,y0),半径为
R
R
R,则圆的参数方程:
- 坐标系 x O y xOy xOy原点平移到 M M M处得到的新坐标系记为 x ′ O ′ y ′ x'O'y' x′O′y′,( O ′ , M O',M O′,M重合)
参数方程
- 以 x ′ O ′ y ′ x'O'y' x′O′y′可建立参数方程 x ′ = R cos θ x'=R\cos\theta x′=Rcosθ, y ′ = R sin θ y'=R\sin\theta y′=Rsinθ;
- 再根据平移的坐标变换公式,
x
′
=
x
−
x
0
x'=x-x_0
x′=x−x0,
y
′
=
y
−
y
0
y'=y-y_0
y′=y−y0,代入上述方程得:
- x − x 0 = R cos θ x-x_0=R\cos\theta x−x0=Rcosθ
- y − y 0 = R sin θ y-y_0=R\sin\theta y−y0=Rsinθ
- 即有方程
(3): θ ∈ [ 0 , 2 π ] \theta\in[0,2\pi] θ∈[0,2π]- x = x 0 + R cos θ x=x_0+R\cos\theta x=x0+Rcosθ
- y = y 0 + R sin θ y=y_0+R\sin\theta y=y0+Rsinθ
一般方程
- x ′ 2 + y ′ 2 = R 2 x'^2+y'^2=R^2 x′2+y′2=R2
- 代入坐标变换公式即有 ( x − x 0 ) 2 + ( y − y 0 ) 2 = R 2 (x-x_0)^2+(y-y_0)^2=R^2 (x−x0)2+(y−y0)2=R2
例
- 圆心 ( − 1 , 2 ) (-1,2) (−1,2),半径为 3 3 3的参数方程: x = − 1 + 3 cos θ x=-1+3\cos\theta x=−1+3cosθ, y = 2 + 3 sin θ y=2+3\sin\theta y=2+3sinθ
交点问题的参数方程法
- 设直线的参数方程为
x
=
1
+
t
x=1+t
x=1+t;
y
=
1
−
t
y=1-t
y=1−t
(1);圆的方程为 x 2 + y 2 = 4 x^2+y^2=4 x2+y2=4(2) - 将(1)代入(2)得: ( 1 + t ) 2 + ( 1 − t ) 2 = 4 (1+t)^2+(1-t)^2=4 (1+t)2+(1−t)2=4;即 2 ( 1 2 + t 2 ) = 4 2(1^2+t^2)=4 2(12+t2)=4, t = ± 1 t=\pm{1} t=±1
- 令 t 1 = − 1 , t 2 = 1 t_1=-1,t_2=1 t1=−1,t2=1,分别代入直线方程,的两个交点 ( 0 , 2 ) (0,2) (0,2), ( 2 , 0 ) (2,0) (2,0)
圆锥曲线的参数方程
- 某些研究领域中,圆锥曲线的参数方程比一般方程更加方便,尤其式椭圆的参数方程应用广泛
椭圆参数方程
- 设椭圆普通方程为 x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a2x2+b2y2=1;即 ( x a ) 2 + ( y b ) 2 = 1 (\frac{x}{a})^2+(\frac{y}{b})^2=1 (ax)2+(by)2=1
- 令 x a = cos t \frac{x}{a}=\cos{t} ax=cost,则 ( y b ) 2 = 1 − cos 2 t = sin 2 t (\frac{y}{b})^2=1-\cos^{2}t=\sin^2{t} (by)2=1−cos2t=sin2t;取 y b = sin t \frac{y}{b}=\sin{t} by=sint
- 得中心在坐标原点时得椭圆参数方程
(1):- x = a cos t x=a\cos{t} x=acost; y = b sin t y=b\sin{t} y=bsint; 0 ∈ [ 0 , 2 π ] 0\in[0,2\pi] 0∈[0,2π]
- 一般位置椭圆:
- 若椭圆中心位于
M
0
(
x
0
,
y
0
)
M_0(x_0,y_0)
M0(x0,y0),则结合坐标平移变换公式得椭圆一般方程
(1-1)- x = x 0 + a cos t x=x_0+a\cos{t} x=x0+acost; y = y 0 + b sin t y=y_0+b\sin{t} y=y0+bsint; t ∈ [ t , 2 π ] t\in[{t},{2\pi}] t∈[t,2π]
- 普通方程: ( x − x 0 ) 2 a 2 + ( y − y 0 ) 2 b 2 = 1 \frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1 a2(x−x0)2+b2(y−y0)2=1
- 若椭圆中心位于
M
0
(
x
0
,
y
0
)
M_0(x_0,y_0)
M0(x0,y0),则结合坐标平移变换公式得椭圆一般方程
例
- 设椭圆方程为
(
x
−
1
)
2
3
+
(
y
+
2
)
2
5
=
1
\frac{(x-1)^2}{3}+\frac{(y+2)^2}{5}=1
3(x−1)2+5(y+2)2=1,求参数方程
- 椭圆中心为 ( 1 , − 2 ) (1,-2) (1,−2), a = 3 , b = 5 a=\sqrt{3},b=\sqrt{5} a=3,b=5,
- 参数方程为 x = 1 + 3 cos θ x=1+\sqrt{3}\cos{\theta} x=1+3cosθ; y = − 2 + 5 sin θ y=-2+\sqrt{5}\sin\theta y=−2+5sinθ, θ ∈ [ 0 , 2 π ] \theta\in[0,2\pi] θ∈[0,2π]
椭圆内接矩形的最大面积问题
- 设椭圆
x
2
5
2
+
y
2
4
2
=
1
\frac{x^2}{5^2}+\frac{y^2}{4^2}=1
52x2+42y2=1,求其内接最大矩形面积
- 椭圆参数方程为 x = 5 cos t x=5\cos{t} x=5cost, y = 4 sin t y=4\sin{t} y=4sint
- 设第一象限内椭圆上一点
M
(
x
,
y
)
M(x,y)
M(x,y),由椭圆的对称性,内接举行的面积为
- S = 4 x y S=4xy S=4xy= 4 × 5 cos t × 4 sin t 4\times{5\cos{t}}\times{4\sin{t}} 4×5cost×4sint= 40 sin 2 t 40\sin{2t} 40sin2t
- 可见,当 t = π 4 t=\frac{\pi}{4} t=4π时, S S S取最大值 40 40 40
- 此时 M M M坐标为 ( 5 2 2 , 2 2 ) (\frac{5}{2}\sqrt{2},2\sqrt{2}) (252,22)
抛物线参数方程
-
设抛物线普通方程为 y 2 = 2 p x y^2=2px y2=2px;
-
只需令 t = y t=y t=y,则 x = y 2 2 p = t 2 2 p x=\frac{y^2}{2p}=\frac{t^2}{2p} x=2py2=2pt2,即得参数方程
(1)- x = t 2 2 p x=\frac{t^2}{2p} x=2pt2; y = t y=t y=t
-
但为了使形式更加协调,通常令 t = 1 2 p y t=\frac{1}{2p}y t=2p1y;即 y = 2 p t y=2pt y=2pt,有方程
(2)- x = 2 p t 2 x=2pt^2 x=2pt2
- y = 2 p t y=2pt y=2pt
一般位置的抛物线
-
由坐标平移变换公式, y = 2 p x y=2px y=2px平移到点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)为定点的位置的曲线方程为 ( y − y 0 ) 2 = 2 p ( x − x 0 ) (y-y_0)^2=2p(x-x_0) (y−y0)2=2p(x−x0)
-
若仅作水平方向的平移,则 y 0 = 0 y_0=0 y0=0,从而方程为 y 2 = 2 p ( x − x 0 ) y^2=2p(x-x_0) y2=2p(x−x0)= 2 p x − 2 p x 0 2px-2px_0 2px−2px0,顶点为 ( x 0 , 0 ) (x_0,0) (x0,0)
- y 2 = 2 p x + α y^2=2px+\alpha y2=2px+α,则 α = − 2 p x 0 \alpha=-2px_0 α=−2px0, x 0 = − α 2 p x_0=-\frac{\alpha}{2p} x0=−2pα
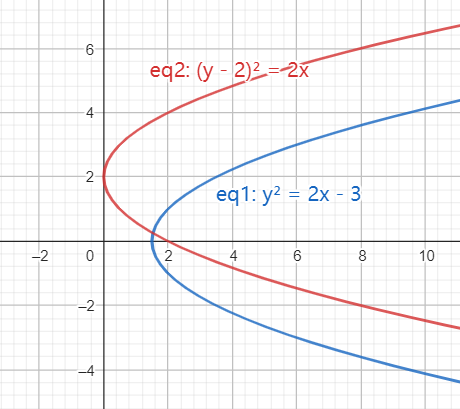
- 例如 y 2 = 2 x − 3 y^2=2x-3 y2=2x−3,变形为 y 2 = 2 x − 2 × 3 2 y^2=2x-2\times{\frac{3}{2}} y2=2x−2×23; ( − 3 = − 2 ) (-3=-2) (−3=−2)
- 即顶点为 ( 3 2 , 0 ) (\frac{3}{2},0) (23,0)的和 y 2 = 2 x y^2=2x y2=2x形状相同的抛物线
-
若仅作竖直方程的平移, ( y − y 0 ) 2 = 2 p x (y-y_0)^2=2px (y−y0)2=2px,顶点为 ( 0 , y 0 ) (0,y_0) (0,y0)
-
对于 ( y + b ) 2 = 2 p x (y+b)^2=2px (y+b)2=2px,其 b = − y 0 b=-y_0 b=−y0, y 0 = − b y_0=-b y0=−b,顶点为 ( 0 , − b ) (0,-b) (0,−b)
-
例如 ( y − 2 ) 2 = 2 x (y-2)^2=2x (y−2)2=2x,其顶点为 ( 0 , 2 ) (0,2) (0,2)
-
-
-
例
- 点
M
(
x
,
y
)
M(x,y)
M(x,y)为
y
2
=
2
x
y^2=2x
y2=2x上的动点,给定
M
0
(
−
1
,
0
)
M_0(-1,0)
M0(−1,0),点
P
P
P为线段
M
0
M
M_0M
M0M的中点;求点
P
P
P的轨迹方程
- 参数方程为: x = 2 t 2 x=2t^2 x=2t2; y = 2 t y=2t y=2t;
- 点
P
(
1
2
(
−
1
+
2
t
2
)
,
1
2
(
0
+
2
t
)
)
P(\frac{1}{2}(-1+2t^2),\frac{1}{2}(0+2t))
P(21(−1+2t2),21(0+2t))=
(
−
1
2
+
t
2
,
t
)
(-\frac{1}{2}+t^2,t)
(−21+t2,t)
- 可见 P P P的轨迹的参数方程为: x = − 1 2 + t 2 x=-\frac{1}{2}+t^2 x=−21+t2; y = t y=t y=t
- 普通方程为 y 2 = x + 1 2 y^2=x+\frac{1}{2} y2=x+21
双曲线的参数方程
- 设中心为坐标原点的双曲线的普通方程为
x
2
a
2
−
y
2
b
2
=
1
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1
a2x2−b2y2=1
(1)- 参考三角恒等式 sec 2 θ − tan 2 θ = 1 \sec^2\theta-\tan^2{\theta}=1 sec2θ−tan2θ=1
- 令
x
a
=
sec
θ
\frac{x}{a}=\sec{\theta}
ax=secθ,
y
b
=
tan
θ
\frac{y}{b}=\tan{\theta}
by=tanθ,得参数方程
(2)- x = a sec θ x=a\sec\theta x=asecθ; y = b tan θ y=b\tan\theta y=btanθ
点到双曲线的最短距离
- 点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)到 x 2 a 2 − y 2 b 2 = 1 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 a2x2−b2y2=1的最短距离问题
例
- 设
M
0
(
0
,
2
)
M_0(0,2)
M0(0,2)到双曲线
x
2
−
y
2
=
1
x^2-y^2=1
x2−y2=1的最小距离
d
d
d
- 双曲线的参数方程为 x = sec θ x=\sec\theta x=secθ; y = tan θ y=\tan\theta y=tanθ
- 设点 M ( sec θ , tan θ ) M(\sec\theta,\tan\theta) M(secθ,tanθ),则 ∣ M 0 M ∣ 2 |M_0M|^2 ∣M0M∣2= ( sec θ − 0 ) 2 + ( tan θ − 2 ) 2 (\sec\theta-0)^2+(\tan\theta-2)^2 (secθ−0)2+(tanθ−2)2= 2 tan 2 θ − 4 tan θ + 5 2\tan^2\theta-4\tan\theta+5 2tan2θ−4tanθ+5= 2 ( tan θ − 1 ) 2 + 3 2(\tan\theta-1)^2+3 2(tanθ−1)2+3
- 可见,当 tan θ − 1 = 0 \tan\theta-1=0 tanθ−1=0时,即 θ = π 4 \theta=\frac{\pi}{4} θ=4π时, ∣ M 0 M ∣ 2 |M_0M|^2 ∣M0M∣2取最小值 3 3 3, ∣ M 0 M ∣ |M_0M| ∣M0M∣取最小值 3 \sqrt{3} 3
- 所以 d = 3 d=\sqrt{3} d=3






![2023年中国氯丁橡胶产量、需求量及进出口现状分析[图]](https://img-blog.csdnimg.cn/img_convert/3b00590f0e73db1b5da8b4a62654a445.png)
![[正式学习java①]——java项目结构,定义类和创建对象,一个标准javabean的书写](https://img-blog.csdnimg.cn/ecd3a19b96fa453fb66bbe827e3458cf.png)

