题目

标题和出处

标题：从前序与中序遍历序列构造二叉树

出处：105. 从前序与中序遍历序列构造二叉树

难度

5 级

题目描述

要求

给定两个整数数组 $\text{preorder}$ 和 $\text{inorder}$，其中 $\text{preorder}$ 是二叉树的前序遍历，$\text{inorder}$ 是同一个树的中序遍历，请构造并返回二叉树。

示例

示例 1：

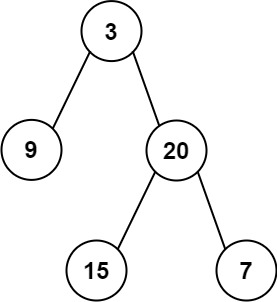
输入：$\text{preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]}$
输出：$\text{[3,9,20,null,null,15,7]}$

示例 2：

输入：$\text{preorder = [-1], inorder = [-1]}$
输出：$\text{[-1]}$

数据范围

• $\text{1}\le \text{preorder.length}\le \text{3000}$
• $\text{inorder.length}=\text{preorder.length}$
• $\text{-3000}\le \text{preorder[i], inorder[i]}\le \text{3000}$
• $\text{preorder}$ 和 $\text{inorder}$ 都由不同的值组成
• $\text{inorder}$ 中的每个值均出现在 $\text{preorder}$ 中
• $\text{preorder}$ 保证为二叉树的前序遍历序列
• $\text{inorder}$ 保证为二叉树的中序遍历序列

解法一

思路和算法

由于二叉树中的每个结点值各不相同，因此可以根据结点值唯一地确定结点。

二叉树的前序遍历的方法为：依次遍历根结点、左子树和右子树，对于左子树和右子树使用同样的方法遍历。

二叉树的中序遍历的方法为：依次遍历左子树、根结点和右子树，对于左子树和右子树使用同样的方法遍历。

前序遍历序列的第一个元素值为根结点值，只要在中序遍历序列中定位到根结点值的下标，即可得到左子树中的结点数和右子树中的结点数。对于左子树和右子树，也可以在给定的前序遍历序列和中序遍历序列中分别得到对应的子序列，根据子序列构造相应的子树。当子树构造完毕时，原始二叉树即可构造完毕。

上述构造二叉树的过程是一个递归分治的过程。将二叉树分成根结点、左子树和右子树三部分，首先构造左子树和右子树，然后构造原始二叉树，构造左子树和右子树是原始问题的子问题。

分治的终止条件是子序列为空，此时构造的子树为空。当子序列不为空时，首先得到根结点值以及左子树和右子树对应的子序列，然后递归地构造左子树和右子树。

实现方面有两点需要注意。

1. 在中序遍历序列中定位根结点值的下标时，简单的做法是遍历整个序列寻找根结点值，该做法的时间复杂度较高。可以使用哈希表存储每个结点值在中序遍历序列中的下标，即可在 $O(1)$ 的时间内定位到任意结点值在中序遍历序列中的下标。

2. 对于左子树和右子树的构造需要使用子序列，此处的子序列实质为下标连续的子数组。为了降低时间复杂度和空间复杂度，使用开始下标和子数组长度确定子数组，则不用新建数组和复制数组元素，而且可以复用哈希表存储的每个结点值在中序遍历序列中的下标信息。

代码

class Solution {
    Map<Integer, Integer> inorderIndices = new HashMap<Integer, Integer>();
    int[] preorder;
    int[] inorder;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        this.inorder = inorder;
        int length = preorder.length;
        for (int i = 0; i < length; i++) {
            inorderIndices.put(inorder[i], i);
        }
        return buildTree(0, 0, length);
    }

    public TreeNode buildTree(int preorderStart, int inorderStart, int nodesCount) {
        if (nodesCount == 0) {
            return null;
        }
        int rootVal = preorder[preorderStart];
        TreeNode root = new TreeNode(rootVal);
        int inorderRootIndex = inorderIndices.get(rootVal);
        int leftNodesCount = inorderRootIndex - inorderStart;
        int rightNodesCount = nodesCount - 1 - leftNodesCount;
        root.left = buildTree(preorderStart + 1, inorderStart, leftNodesCount);
        root.right = buildTree(preorderStart + 1 + leftNodesCount, inorderRootIndex + 1, rightNodesCount);
        return root;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是数组 $\text{preorder}$ 和 $\text{inorder}$ 的长度，即二叉树的结点数。将中序遍历序列中的每个结点值与下标的对应关系存入哈希表需要 $O(n)$ 的时间，构造二叉树也需要 $O(n)$ 的时间。

• 空间复杂度：$O(n)$，其中 $n$ 是数组 $\text{preorder}$ 和 $\text{inorder}$ 的长度，即二叉树的结点数。空间复杂度主要是递归调用的栈空间以及哈希表空间，因此空间复杂度是 $O(n)$。

解法二

思路和算法

使用迭代的方法构造二叉树，需要充分利用二叉树遍历的性质，考虑遍历序列中相邻结点的关系。

对于前序遍历序列中的两个相邻的值 $x$ 和 $y$，其对应结点的关系一定是以下两种情况之一：

1. 结点 $y$ 是结点 $x$ 的左子结点；

2. 结点 $x$ 没有左子结点，结点 $y$ 是结点 $x$ 的右子结点，或者结点 $y$ 是结点 $x$ 的某个祖先结点的右子结点。

对于第 1 种情况，在中序遍历序列中，$y$ 在 $x$ 前面且 $y$ 和 $x$ 相邻。对于第 2 种情况，在中序遍历序列中，$x$ 在 $y$ 前面。

判断前序遍历序列中的两个相邻的值属于哪一种情况，需要借助中序遍历序列。由于中序遍历访问右子树在访问根结点之后，因此可以比较前序遍历序列的上一个结点值和中序遍历序列的当前结点值，判断属于哪一种情况：

• 如果前序遍历序列的上一个结点值和中序遍历序列的当前结点值不同，则前序遍历序列的上一个结点有左子结点，属于第 1 种情况；

• 如果前序遍历序列的上一个结点值和中序遍历序列的当前结点值相同，则前序遍历序列的上一个结点没有左子结点，属于第 2 种情况。

注意在第 1 种情况下，中序遍历序列的结点值顺序恰好和前序遍历序列的结点值顺序相反，可以使用栈实现反转序列。

具体做法是，遍历前序遍历序列，对于每个值分别创建结点，将每个结点作为上一个结点的左子结点，并将每个结点入栈，直到前序遍历序列的上一个结点值等于中序遍历序列的当前结点值。然后遍历中序遍历序列并依次将栈内的结点出栈，直到栈顶结点值和中序遍历序列的当前结点值不同，此时前序遍历序列的当前值对应的结点为最后一个出栈的结点的右子结点，将当前结点入栈。然后对前序遍历序列和中序遍历序列的其余值继续执行上述操作，直到遍历结束时，二叉树构造完毕。

以下用一个例子说明构造二叉树的过程。已知二叉树的前序遍历序列是 $[1,10,8,9,5,7,15,12,20,13]$，中序遍历序列是 $[9,5,8,10,7,1,12,15,13,20]$，二叉树如图所示。

初始时，中序遍历序列的下标是 $0$。以下将中序遍历序列的下标处的值称为中序遍历序列的当前结点值。

1. 将前序遍历序列的下标 $0$ 的元素 $1$ 作为根结点值创建根结点，并将根结点入栈。

2. 当遍历到前序遍历序列的 $10$ 时，上一个结点值和中序遍历序列的当前结点值不同，因此创建结点 $10$，作为结点 $1$ 的左子结点，并将结点 $10$ 入栈。

3. 当遍历到前序遍历序列的 $8$ 时，上一个结点值和中序遍历序列的当前结点值不同，因此创建结点 $8$，作为结点 $10$ 的左子结点，并将结点 $8$ 入栈。

4. 当遍历到前序遍历序列的 $9$ 时，上一个结点值和中序遍历序列的当前结点值不同，因此创建结点 $9$，作为结点 $8$ 的左子结点，并将结点 $9$ 入栈。

5. 当遍历到前序遍历序列的 $5$ 时，上一个结点值是 $9$，和中序遍历序列的当前结点值相同，因此遍历中序遍历序列并将栈内的结点 $9$ 出栈，此时中序遍历序列的下标移动到 $1$。创建结点 $5$，将结点 $5$ 作为结点 $9$ 的右子结点，并将结点 $5$ 入栈。

6. 当遍历到前序遍历序列的 $7$ 时，上一个结点值是 $5$，和中序遍历序列的当前结点值相同，因此遍历中序遍历序列并将栈内的结点 $5$、$8$、$10$ 出栈，此时中序遍历序列的下标移动到 $4$。创建结点 $7$，将结点 $7$ 作为结点 $10$ 的右子结点，并将结点 $7$ 入栈。

7. 当遍历到前序遍历序列的 $15$ 时，上一个结点值是 $7$，和中序遍历序列的当前结点值相同，因此遍历中序遍历序列并将栈内的结点 $7$、$1$ 出栈，此时中序遍历序列的下标移动到 $6$。创建结点 $15$，将结点 $15$ 作为结点 $1$ 的右子结点，并将结点 $15$ 入栈。

8. 当遍历到前序遍历序列的 $12$ 时，上一个结点值和中序遍历序列的当前结点值不同，因此创建结点 $12$，作为结点 $15$ 的左子结点，并将结点 $12$ 入栈。

9. 当遍历到前序遍历序列的 $20$ 时，上一个结点值是 $12$，和中序遍历序列的当前结点值相同，因此遍历中序遍历序列并将栈内的结点 $12$、$15$ 出栈，此时中序遍历序列的下标移动到 $8$。创建结点 $20$，将结点 $20$ 作为结点 $15$ 的右子结点，并将结点 $20$ 入栈。

10. 当遍历到前序遍历序列的 $13$ 时，上一个结点值和中序遍历序列的当前结点值不同，因此创建结点 $13$，作为结点 $20$ 的左子结点，并将结点 $13$ 入栈。

此时遍历结束，二叉树构造完毕。

代码

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int length = preorder.length;
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < length; i++) {
            TreeNode prev = stack.peek();
            TreeNode curr = new TreeNode(preorder[i]);
            if (prev.val != inorder[inorderIndex]) {
                prev.left = curr;
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    prev = stack.pop();
                    inorderIndex++;
                }
                prev.right = curr;
            }
            stack.push(curr);
        }
        return root;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是数组 $\text{preorder}$ 和 $\text{inorder}$ 的长度，即二叉树的结点数。前序遍历序列和中序遍历序列各需要遍历一次，构造二叉树需要 $O(n)$ 的时间。

• 空间复杂度：$O(n)$，其中 $n$ 是数组 $\text{preorder}$ 和 $\text{inorder}$ 的长度，即二叉树的结点数。空间复杂度主要是栈空间，取决于二叉树的高度，最坏情况下二叉树的高度是 $O(n)$。