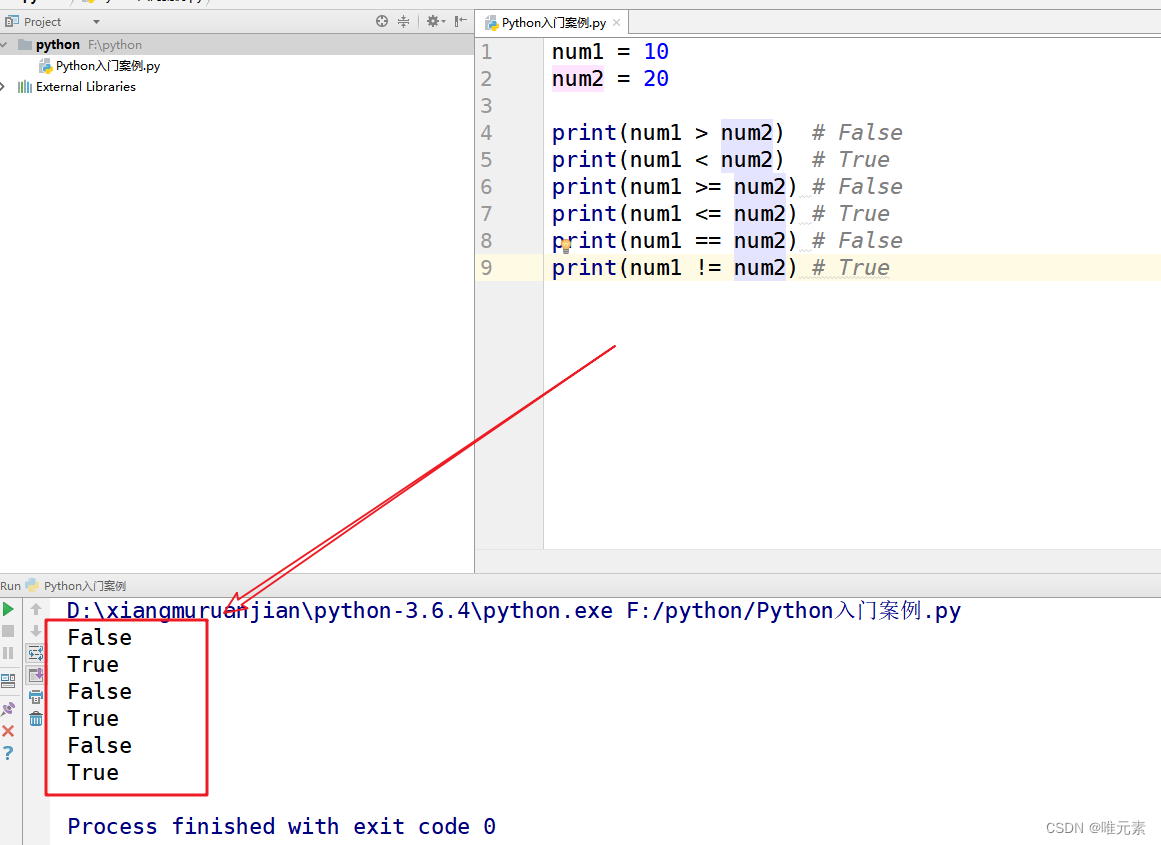
论文链接:https://openreview.net/forum?id=OOsR8BzCnl5
https://arxiv.org/abs/2102.02051
代码链接:https://github.com/hanmenghan/TMC
Zongbo Han, Changqing Zhang, Huazhu Fu, Joey Tianyi Zhou, Trusted Multi-View Classification, International Conference on Learning Representations (ICLR) 2021
作者另外一篇结合不确定性与 mix up 的相关文章
UMIX: Improving Importance Weighting for Subpopulation Shift via Uncertainty-Aware Mixup
1. 方法动机
1.1. 方法动机
多模态人工智能技术正在被广泛应用到智能医疗、无人系统等重要领域,设计精准、可靠的多模态学习技术成为支持重要应用的关键。
多模态数据为智能系统决策提供了丰富信息,使得多模态智能系统可以 “兼听则明”,提高分类和预测准确性。
然而,在许多代价敏感场景中,多模态融合及决策的可信性往往更加重要。
对于多模态分类任务,传统方法通常假设各模态质量和任务相关性是稳定的。
但实际上,对于不同样本或在不同场景下,模态的质量和任务的相关程度往往具有动态性。如多传感器场景中,RGB 图像在光线好时更有效,而近红外图像在可以在视觉困难情况下提供更重要的信息。
多模态医学诊断中,往往存在多项检查数据,对于不同患者同一检查项目所提供信息的重要性也会有所不同。此外,传感器的不稳定以及损坏导致数据获取异常,也给融合带来挑战。考虑到多模态数据质量的动态性,需要使多模态智能系统可以做到可靠而且有证据地融合多模态信息,即 “信而有征”,从而提高分类和预测的稳定性和可信性。
本文使用不确定性对此动态性进行建模、利用一种改进的证据融合策略集成多模态信息。论文题为 Trusted Multi-View Classification ,现已被 ICLR 2021 收录。
基于此,不仅能在模态质量动态变化时获得更加稳定的分类结果,同时能够估计决策信心,并对分类结果和分类信心进行模态级溯源。整体上,所提方法在多模态协同学习(兼听则明)中,对不同模态进行证据估计(信而有征),从而支持融合及决策的可靠性和稳定性。
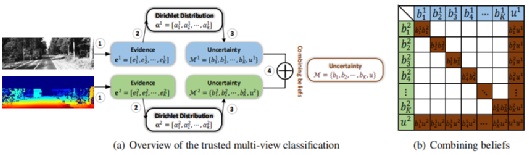
1.2
1.3
2. proposed method
2.1 不确定性和证据理论
在使用 softmax 的分类模型中,最大的 softmax 输出用于最终预测会使即使错误的预测也有较高的置信度(over-confident)。
主观逻辑(subjective logic)算法能够很好的解决这一问题。与普通的分类不同,主观逻辑通过将输出建模为狄利克雷分布来获得不同类的分配概率和不确定性。
具体地,对于视图 ,我们有,
其中 表示不确定性, 表示第 类的分配概率。对第 个视图,主观逻辑将证据 和狄利克雷分布的参数
进行了联系,即
。然后,不同类的分配概率和不确定性可以由以下公式计算得到:
其中,
2.2 DS 组合规则用于多模态分类
DS 组合规则用于多模态分类
对于模态 可以得到图片,现在考虑使用 DS 组合规则将 个独立的模态所得到的分配概率进行组合。
给定 和 ,可以使用以下规则进行融合:
具体的计算方式为:
其中 反映了 和 的冲突程度。
根据 DS 组合规则的可传递性,我们可以得到,对于 个模态的融合方式:
.
该组合方式具有较好的合理性和可解释性。不同类的分配概率和不确定性计算的过程实际保证了如下特性:(1)观测到的第 类的证据越多,分配给第 类的可能性就越大,反之亦然;(2)若所有类证据都不足,则整体不确定性较大。此外,目标函数还通过抑制错误标签对应的证据避免不确定性小但分类错误的情况。
通过学习获得
2.3 通过学习获得 M
传统神经网络通常使用交叉熵损失进行训练:
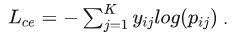
由于模型的输出为狄利克雷分布,需要对其进行调整,得到下式:
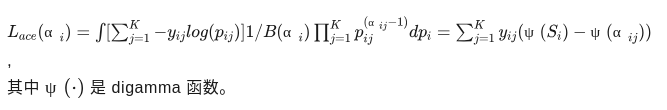
其中 ψ 是 digamma 函数。
上述损失能够促进模型每个样本的正确标签比其他类生成更多的证据,但是不能保证错误类的证据尽量少。我们期望对于错误分类的样本的证据变为 0。因此以下损失函数被引入用来对证据进行正则化。
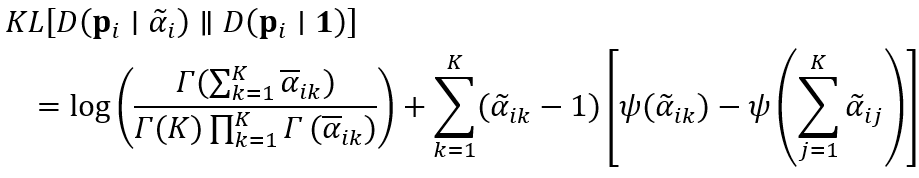
给出狄利克雷分布参数 后的损失可以写作:
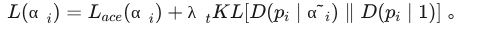
在多模态框架下,我们采用多任务策略,总损失如下所示:
3.3. 实验结果
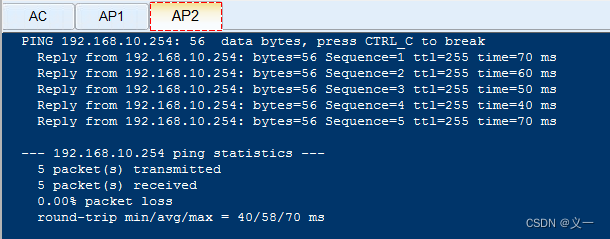
实验表明,所提方法可以较为灵敏地感知噪声的动态变化 (更多实验见论文):
3.1 实验分析
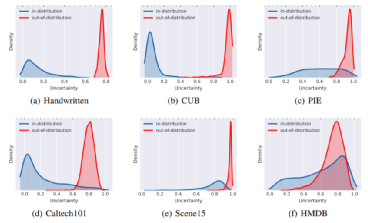
图 2. 不确定性密度分布:分布内 / 外样本对比.

图 3. 典型确定性和不确定性分类结果.
3.2 小结
针对多模态之间关系的不稳定性或动态性,此次研究首次提出可信多模态融合方法,设计了支持可信和可解释的多模态分类算法。
所提出的模型基于证据理论以可学习方式进行自适应的动态集成,对每个样本的每个模态进行不确定性估计,使模型能够在复杂多变场景下保证分类的可靠性和稳定性。
3.3 应用场景
潜在应用场景主要包括:
-
需要可信决策的多模态分类任务,如智能医疗、自动驾驶等代价敏感任务;
-
模态质量动态变化的应用场景;
-
寻求决策可溯源的多模态集成场景;
-
多传感器系统中容易出现传感器故障的场景。