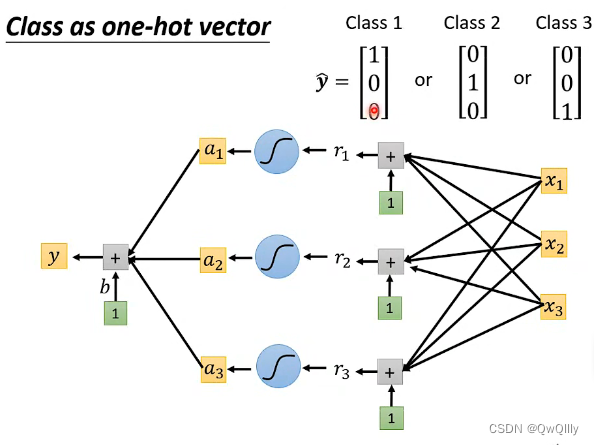
一、实例回顾

分类的例子在前几讲中已详细分析，此处略过。

 

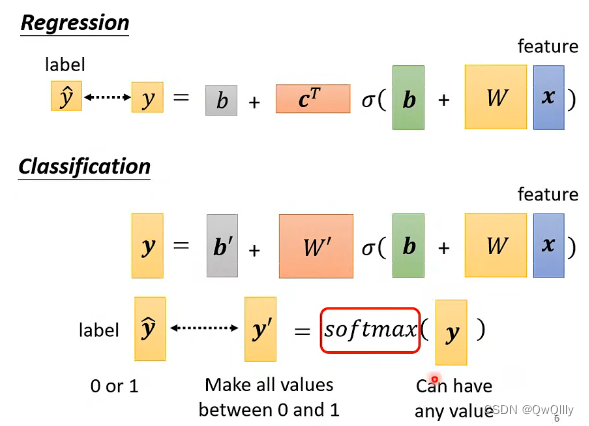
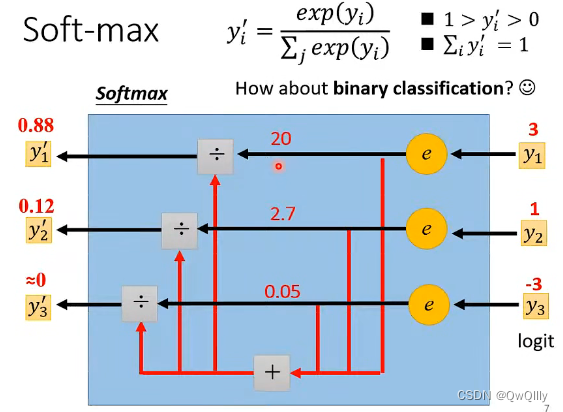
二、softmax与sigmoid

此处要明白！softmax和sigmoid的区别和联系

Softmax函数和Sigmoid函数的区别与联系 - 知乎 (zhihu.com)

Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值。

Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。

Softmax函数是二分类函数Sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

对于二分类问题来说，理论上，两者是没有任何区别的。由于我们现在用的Pytorch、TensorFlow等框架计算矩阵方式的问题，导致两者在反向传播的过程中还是有区别的。实验结果表明，两者还是存在差异的，对于不同的分类模型，可能Sigmoid函数效果好，也可能是Softmax函数效果。

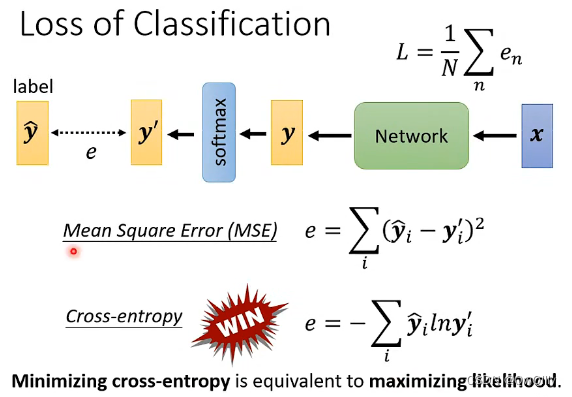
三、损失函数

最小化交叉熵就是最大化对数似然函数

最小化交叉熵损失与极大似然 - 知乎 (zhihu.com)

下面给出极大似然估计与最小化交叉熵损失的转化过程，意在说明在伯努利分布下，极大似然估计与最小化交叉熵损失其实是同一回事。

下面同样给出极大似然估计与最小化广义伯努利分布的交叉熵损失函数的转化过程，意在说明在广义伯努利分布下，极大似然估计与最小化交叉熵损失也是同一回事。

实例说明

此时简单举例说明：更改loss function后，不会被困住了。

交叉熵形式使优化问题变得简单 

MSE左上角的梯度变化非常平缓，接近于0，被困住。