题目一
试题编号: 202209-1
试题名称: 如此编码
时间限制: 1.0s
内存限制: 512.0MB
问题描述:
题目背景
某次测验后,顿顿老师在黑板上留下了一串数字 23333 便飘然而去。凝望着这个神秘数字,小 P 同学不禁陷入了沉思……
题目描述
已知某次测验包含 n 道单项选择题,其中第 i 题(1≤i≤n)有 ai 个选项,正确选项为 bi,满足 ai≥2 且 0≤bi<ai。比如说,ai=4 表示第 i 题有 4 个选项,此时正确选项 bi 的取值一定是 0、1、2、3 其中之一。
顿顿老师设计了如下方式对正确答案进行编码,使得仅用一个整数 m 便可表示 b1,b2,⋯,bn。
首先定义一个辅助数组 ci,表示数组 ai 的前缀乘积。当 1≤i≤n 时,满足:
ci=a1×a2×⋯×ai
特别地,定义 c0=1。
于是 m 便可按照如下公式算出:

易知,0≤m<cn,最小值和最大值分别当 bi 全部为 0 和 bi=ai−1 时取得。
试帮助小 P 同学,把测验的正确答案 b1,b2,⋯,bn 从顿顿老师留下的神秘整数 m 中恢复出来。
输入格式
从标准输入读入数据。
输入共两行。
第一行包含用空格分隔的两个整数 n 和 m,分别表示题目数量和顿顿老师的神秘数字。
第二行包含用空格分隔的 n 个整数 a1,a2,⋯,an,依次表示每道选择题的选项数目。
输出格式
输出到标准输出。
输出仅一行,包含用空格分隔的 n 个整数 b1,b2,⋯,bn,依次表示每道选择题的正确选项。
样例1输入
15 32767
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
样例1输出
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
样例2输入
4 0
2 3 2 5
样例2输出
0 0 0 0
样例3输入
7 23333
3 5 20 10 4 3 10
样例3输出
2 2 15 7 3 1 0
样例3解释

提示
对任意的 1≤j≤n,因为 cj+1,cj+2,⋯ 均为 cj 的倍数,所以 m 除以 cj 的余数具有如下性质:
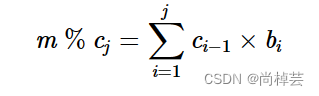
其中 % 表示取余运算。令 j 取不同的值,则有如下等式:
m % c1 = c0×b1
m % c2 = c0×b1+c1×b2
m % c3 = c0×b1+c1×b2+c2×b3⋯
题目分析(个人理解)
- 此题可以理解为一个加密解密的过程,测验的正确答案bn在m中,现在要输出正确答案,还是先看输入,第一行输入n个题目和m的值,之后输入每道题有几个选项(用空格分开)。
- 我还是选择列表存储,这道题关键是理解解密的过程,这个过程就是给出m推导出b的值,在题目的提示部分已经告诉我们了,当i=3时m % c3 = c0×b1+c1×b2+c2×b3那么求b3只需要m%3之后减去c2之前的部分然后对c2取整即可。
- 上代码!!!
# 输入n题目数量和m神秘数字
n, m = map(int, input().split())
# 输入n道选择题的选项数字
a = list(map(int, input().split()))
# 设置b数组来存放每道选择题的正确选项
b = []
# c为c0,初始值为1
c = 1
# tc为辅助值,即为t的下一个值
tc = 1
# temp为辅助值,为记录除了此次的C*B之前所有C*B的值的和
temp = 0
# 通过循环进行每道题答案的更新
for i in a:
# 将tc的值进行更新为此时c的下一个值
tc = i*c
# 向b数组中添加此时题目的正确选项
b.append((m%tc-temp)//c)
# 更新temp的值
temp += c*b[-1]
# 更新c的值
c = tc
# 输出每道题的正确选项
print(*b)
题目二
试题编号: 202209-2
试题名称: 何以包邮?
时间限制: 1.0s
内存限制: 512.0MB
问题描述:
题目描述
新学期伊始,适逢顿顿书城有购书满 x 元包邮的活动,小 P 同学欣然前往准备买些参考书。
一番浏览后,小 P 初步筛选出 n 本书加入购物车中,其中第 i 本(1≤i≤n)的价格为 ai 元。
考虑到预算有限,在最终付款前小 P 决定再从购物车中删去几本书(也可以不删),使得剩余图书的价格总和 m 在满足包邮条件(m≥x)的前提下最小。
试帮助小 P 计算,最终选购哪些书可以在凑够 x 元包邮的前提下花费最小?
输入格式
从标准输入读入数据。
输入的第一行包含空格分隔的两个正整数 n 和 x,分别表示购物车中图书数量和包邮条件。
接下来输入 n 行,其中第 i 行(1≤i≤n)仅包含一个正整数 ai,表示购物车中第 i 本书的价格。输入数据保证 n 本书的价格总和不小于 x。
输出格式
输出到标准输出。
仅输出一个正整数,表示在满足包邮条件下的最小花费。
样例1输入
4 100
20
90
60
60
样例1输出
110
样例1解释
购买前两本书(20+90)即可包邮且花费最小。
样例2输入
3 30
15
40
30
样例2输出
30
样例2解释
仅购买第三本书恰好可以满足包邮条件。
样例3输入
2 90
50
50
样例3输出
100
样例3解释
必须全部购买才能包邮。
子任务
70% 的测试数据满足:n≤15;
全部的测试数据满足:n≤30,每本书的价格 ai≤104 且 x≤a1+a2+⋯+an。
提示
对于 70% 的测试数据,直接枚举所有可能的情况即可。
题目分析(个人理解)
- 注意题目条件,有两个判断要求,第一个要求满足包邮条件,第二个要求在第一个要求的基础上使得总价格最小;但是为了方便我可以先将每次拿一次书之后的总价格最小值都存下来(记忆化),就是每拿一本,就从新按照价格最便宜的先选,依次重新排序选择,一直选到第n个, 然后再去判断是否满足包邮条件即可。
- 这里这是一个重叠子问题,(子问题是原大问题的小版本,他们计算步骤完全一样,可以和递归联系起来)一个子问题多次计算耗费大量时间,用动态规划处理,每个子问题只需要计算一次,从而避免重复计算,具体的做法是,先分析得到最优子结构,然后用递推或者带记忆化搜索的递归进行实现。
- 先定义一个数组dp=[]大小就是N*X。用来储存每一个价格的最小花费,然后将每本书的价格存入列表a[]。第二步将每多拿一本书的之后的价格最小值都存入dp中,最后遍历dp如果大于等于X,也就是满足了包邮条件那么就直接输出当前dp[i]即可。
- 尤其注意实现自我滚动的时候,j是反过来循环的,就是从后面往前面覆盖。
- 上代码!!!
# 输入购物车中的图书数量n和包邮最低值x
n, x = map(int,input().split())
# 设置a来存储每个书的价格
a = []
# 设置动态规划数组存储每个价格的最小花费
dp = [0]*(n*x)
# 进行遍历,将每本书的价格依次存入a
for i in range(n):
t = int(input())
a.append(t)
# 设置pre来保存目前满足包邮的最小花费
pre = sum(a)
# 01背包解法,将每个地方的最优解存入dp数组中
for i in range(n):
for j in range(pre,a[i]-1,-1):#自我滚动
dp[j] = max(dp[j],dp[j-a[i]]+a[i])
# 从x开始遍历,找到超过x的dp[i]
for i in range(x,pre+1):
if dp[i]>=x:
print(dp[i])
break
总结
又又又要补一期动态规划的内容。