题目

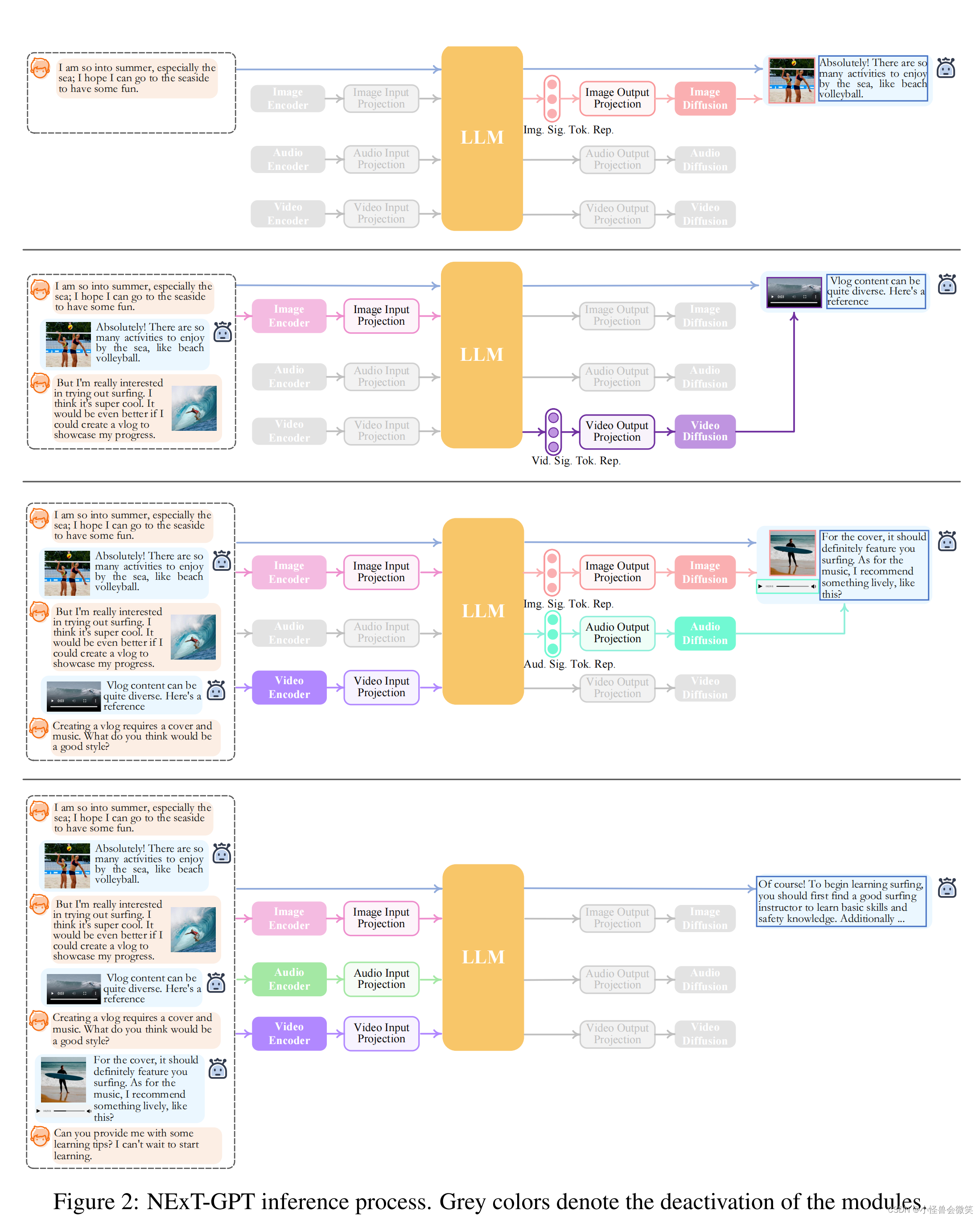
t(t<=1e6)组样例，每次给定一个n(n<=1e9)，统计边长为n的上述三角形的等边三角形个数

其中等边三角形的三个顶点，可以在所有黑色三角形&白色三角形的顶点中任取，

答案对1e9+7取模

思路来源

申老师 & oeis A000332

Solution to Problem #3

题解

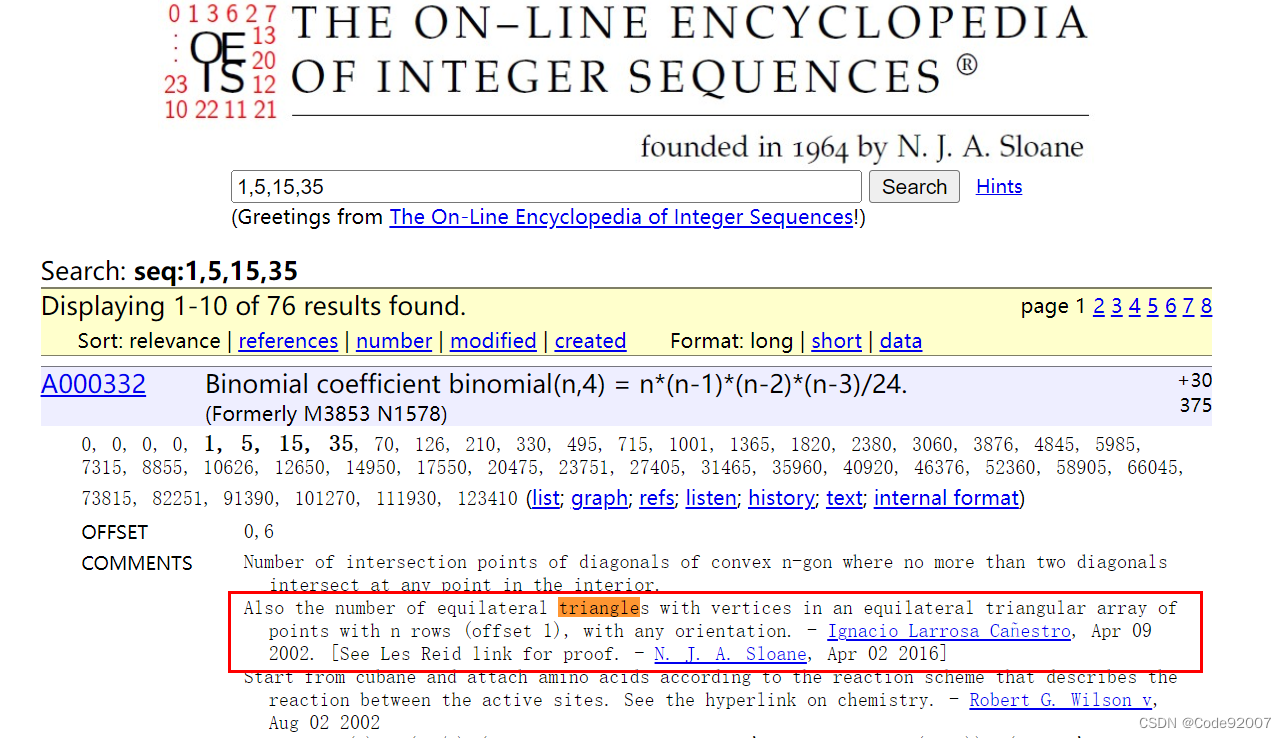
oeis打一下前四项的表，发现是C(n,4)，并且还有说明，

是等于长度为n时的等边三角形，任取顶点时，不限边长大小的等边三角形个数

看了一下证明，感觉也是变相计数，这里提供一种计数方式，可能赛中还是会选择打表吧

计数方式

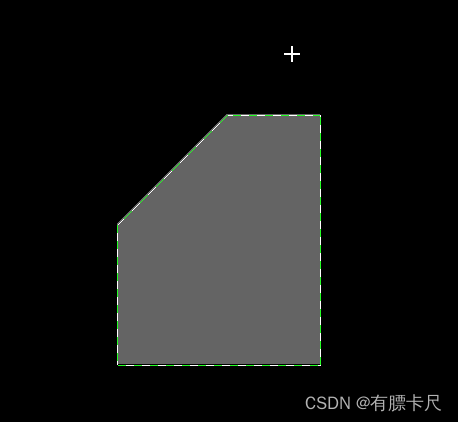
对于边长为n的三角形，三个点都在三角形的三条边上的方案，恰有n种

图示分别对应n=2,3,4的情形，

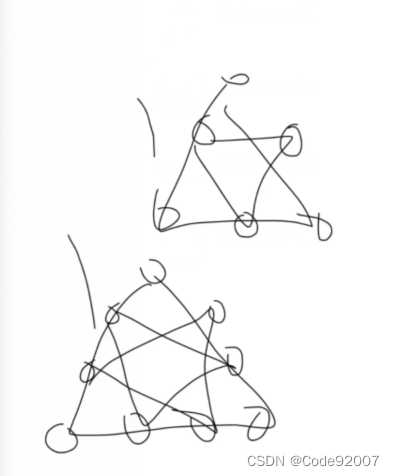
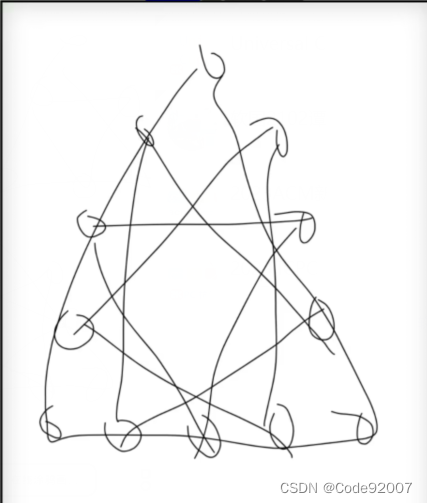
所以，可以枚举每个边长i，统计边长=i的正向的三角形的个数，每个的贡献是i

因为倒立的边长为i的三角形，会在正向为2*i的三角形中被枚举到，所以忽略

归纳/找规律可发现，边长为n-i+1的正向三角形的出现次数是i*(i+1)/2，有下式成立：

恒等式的组合意义

从n+3个数选4个数时，可以枚举第三个数的位置，左边i+1个位置选2个，右边选1个

但是确实没有看出来其与三角形选择方法的关联关系

代码

输出C(n+3,4)即可，即(n+3)*(n+2)*(n+1)*n/24

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pb push_back
#define all(a) a.begin(),a.end()
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
std::mt19937_64 gen(std::chrono::system_clock::now().time_since_epoch().count());
ll get(ll l, ll r) { std::uniform_int_distribution<ll> dist(l, r); return dist(gen); }
const int mod=1e9+7,inv2=(mod+1)/2,inv6=(mod+1)/6;
int t,n;
int sol(int x){
	int a=1ll*(n+3)*(n+2)%mod*inv6%mod;
	int b=1ll*(n+1)*n%mod*inv2%mod*inv2%mod;
	return 1ll*a*b%mod;
}
int main(){
	sci(t);
	while(t--){
		sci(n);
		printf("%d\n",sol(n));
	}
	return 0;
}