大家好,今天本文将展示如何从零开始实现神经网络的最基本要素(感知器),以及人工智能的基本模块背后的数学原理。
虽然人工智能和机器学习等术语已经成为流行词汇,每天都会听到或谈论这些概念,但它们背后的数学概念已经存在了很长时间(从40年代起就有介绍人工神经网络-ANN的论文)。其有几个很好的优势:
-
现在有大量的数据可用于训练神经网络,而且在处理大型、复杂的问题上,人工神经网络经常优于其他机器学习技术。
-
自20世纪90年代以来,计算能力大幅增加,现在可以在合理的时间内训练大型神经网络。这在一定程度上归功于摩尔定律,但在另一方面也要感谢游戏行业,他们生产了数以百万计功能强大的GPU卡。
-
训练算法已经得到改进。平心而论,它们与20世纪90年代使用的算法只有细微的不同,但这些相对较小的调整产生了巨大的积极影响。
一、简介
感知器是神经网络的基本构建模块,为我们提供了对机器学习和人工智能世界的简单而强大的了解。本文将探索感知器的本质,并学习如何从零开始实现它们。感知器在人工智能的发展中具有重要的历史意义,为现代深度学习模型奠定了基础。感知器在概念上的简单性使其成为任何希望掌握神经网络基础知识的人的理想起点。
接下来,本文将深入探讨感知器的架构和内部工作原理,提供代码示例和实用见解,以确保你对这一基本概念有扎实的理解。因此,接下来将使用以下Python软件包来实现感知器。
import numpy as np
import matplotlib.pyplot as plt
import random
import math二、感知器架构
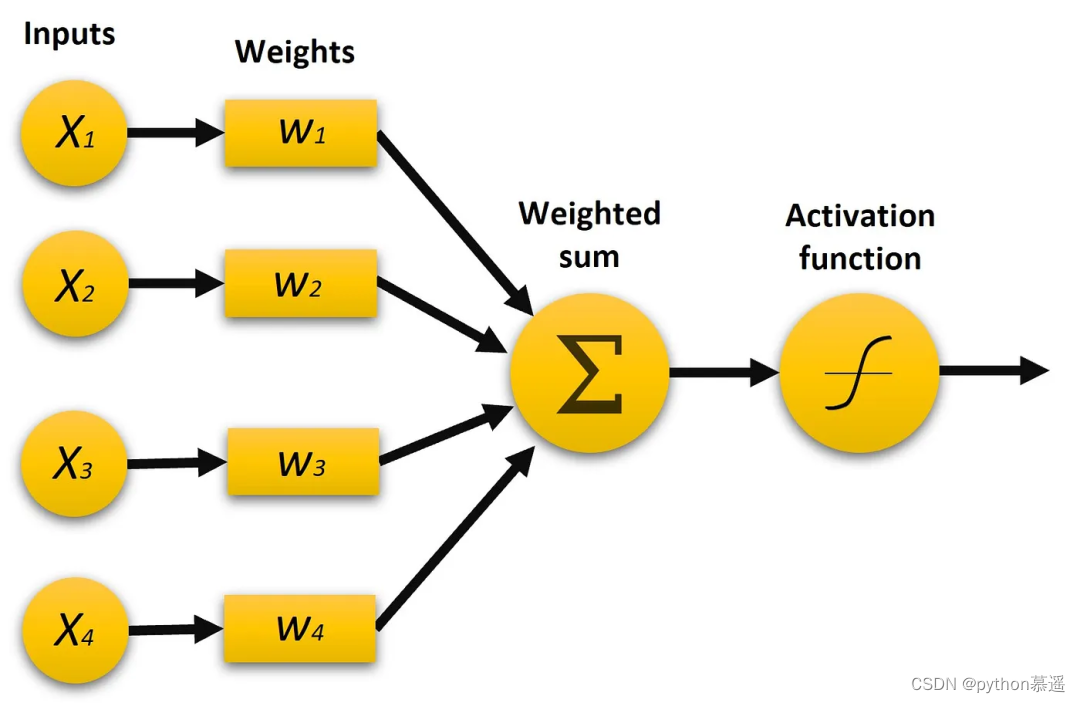
感知器由以下核心部件组成:
1. 输入特征
输入特征代表感知器用于做出决策的原始数据,本文将定义两个具有固定值的输入(X1、X2),以简化神经网络。然而在实际应用中,神经元可能会使用多个输入来表示不同的输入信息。
X = [1, 0]
2. 权重
在此本文将生成用于组成神经网络的权重,我们将首先生成较小的随机权重,但需要注意的是,这些权重将在网络训练时更新。下面的代码展示了如何生成两个介于-1和1之间的随机权重(每个输入一个)。
w = []
nInputs = 2
for i in range(nInputs):
w.append(random.uniform(-1, 1))
3. 偏置
偏置项是感知器的附加输入项,用作可调节的阈值,它允许感知器在所有输入特征为零时也能做出决策。偏置有助于控制感知器的激活,本文将初始偏置设置为一个小的随机数。
b = random.uniform(-1,1)
4. 激活函数
激活函数将加权输入的总和转换为二进制输出,该输出是感知器的预测结果,表示一个决策或分类,通常我们希望激活函数的输出为0或1。另一个关键属性是其可微分性,这在网络训练中起着至关重要的作用。函数的可微分性是在训练过程中调整网络权重的不可或缺的要求,使网络能够从数据中学习并随着时间的推移进行改进。
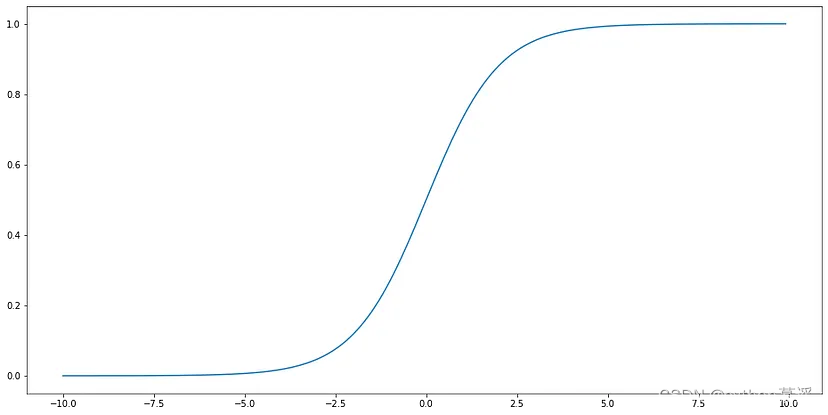
用于此目的的一个非常常见的函数是sigmoid函数,因为它具有可微分性、平滑性和简单的梯度。
def sigmoid(x):
return 1/(1+math.exp(-x))
5. 前馈
现在我们已经掌握了设计感知器的基本元素,我们必须将输入数据传递给感知器,这一步称为前馈。首先我们计算输入数据的加权和,然后将结果通过激活函数传递给感知器。
加权和只是权重向量和输入之间的点积,然后将其传递给sigmoid函数:
# 加权和 = w1*x1 + w2*x2 ... + b
z = sigmoid(np.dot(X, w) + b)
最后必须应用激活函数来预测输出为0还是1:
def activation(z):
return 1 if z >0.5 else 0三、训练感知器
到目前为止,我们只能将输入数据传递给感知器,而不知道感知器是否正确。训练阶段对于提高感知器的准确性至关重要,其过程包括对感知器的权重进行多次迭代(epochs)更新。在每个迭代中,我们都要计算输出相对于目标实际值的误差,以便更新权重并使误差最小化:
y_pred = activation(z)
error = y - y_pred
lr = 0.1
w_new = []
for wi, xi in zip(w, X):
w_new.append(wi + lr*error*xi)
b_new = b + lr*error
其中,lr是学习率,我们将其值设置为0.1,但也可以根据问题的不同设置为其他值。
因此我们现在拥有更新的权重,重复执行前馈步骤多个周期。通过根据梯度反复调整权重和偏置,网络会逐渐学会做出更好的预测,并随着时间的推移减少误差,这一步骤也被称为反向传播。
四、应用于鸢尾花数据集
到目前为止,大家已经了解感知器的各个部分以及它们的工作原理。接下来,本文将汇总所有学到的知识,创建感知器类,并使用真实数据集来验证感知器的工作原理。
【鸢尾花数据集】:https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html
class Perceptron():
def __init__(self,input_size = 2, lr = 0.01, epochs = 20):
# 设置默认参数
self.lr = lr
self.epochs = epochs
self.input_size = input_size
self.w = np.random.uniform(-1, 1, size=(input_size))
self.bias = random.uniform(-1,1)
self.misses = []
def predict(self, X):
w = self.w
b = self.bias
z = sigmoid(np.dot(X,self.w) + b)
if z > 0.5:
return 1
else:
return 0
def fit(self, X, y):
for epoch in range(self.epochs):
miss = 0
for yi, xi in zip(y, X):
y_pred = self.predict(xi)
# 更新权重以最小化误差
error = yi - y_pred
self.w += self.lr*error*xi
self.bias += self.lr*error
miss += int(error != 0.0)
# 获取每个时期的错误分类数
self.misses.append(miss)
从上面的代码中可以看出:
-
lr:学习率 -
input_size:输入数据的特征数量 -
epochs:训练的迭代次数 -
X:输入数据(样本,特征) -
y:目标数据(标签0或1)
现在,我们将使用scikit-learn库中鸢尾花数据集的感知器实现:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
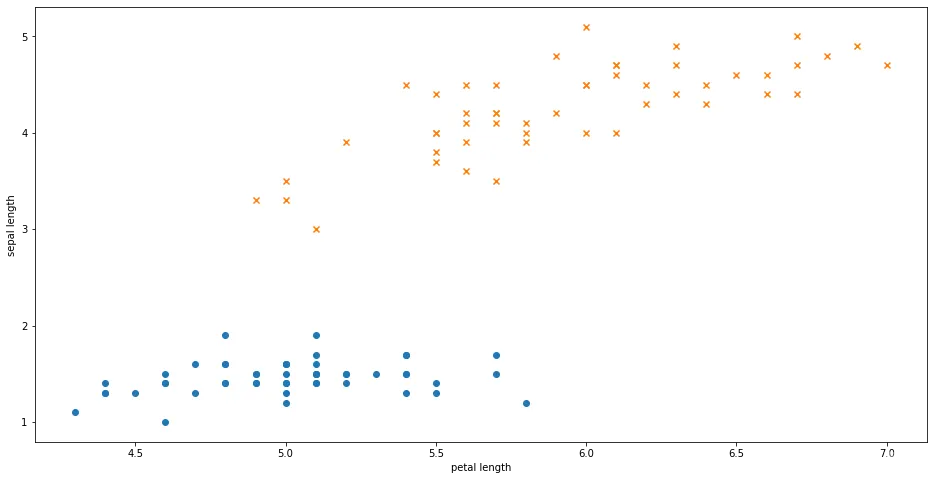
该数据集由4个特征(花萼长度、花萼宽度、花瓣长度和花瓣宽度)组成,共有150个样本,分为3个分类(山鸢尾、变色鸢尾和维吉尼亚鸢尾)。为了简化起见,本示例只使用2个特征(花萼长度和花瓣长度)以及山鸢尾和变色鸢尾的样本:
X = X[:100, [0,2]]
y = y[y<2]
# 绘制数据
plt.figure(figsize=(16,8))
plt.scatter(X[:50,0], X[:50,1], marker='o', label='setosa')
plt.scatter(X[50:,0], X[50:,1], marker='x', label='virginica')
plt.ylabel('sepal length')
plt.xlabel('petal length')
plt.show()
接下来,我们需要使用标记的数据(X,y)来训练感知器,并查看其性能表现如何:
perceptron = Perceptron()
perceptron.fit(X,y)
print(perceptron.w, perceptron.bias)
#(array([0.09893529, 0.09323132]), -0.763184789232628)
这样,我们就得到了训练的最优权重和偏置。那么感知器在错误分类方面表现如何呢?为此,我们将绘制感知器类别的错误参数:
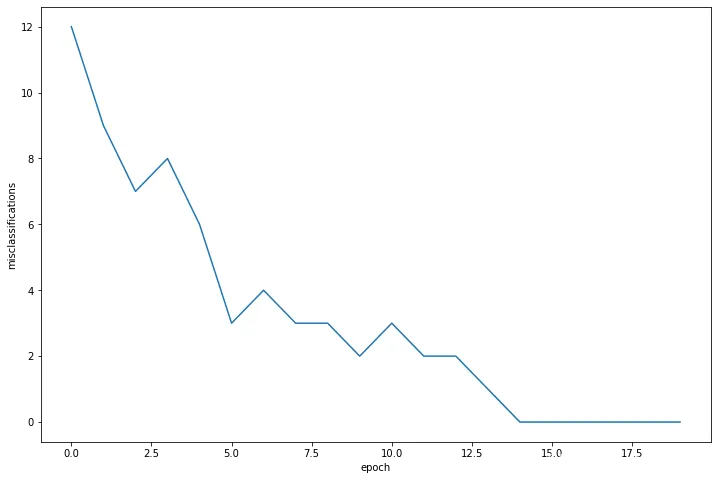
感知器在训练过程中的错误分类次数
从上图可以看出,感知器在第一个时期出现了12次失误,并持续学习,直到在训练结束时不再犯错。
五、总结
本文成功地实现并训练了一个感知器,并使用真实数据集对其性能进行了评估。
尽管感知器是神经网络的基础模块,但正如我们在文章中所看到的,它也有其局限性:
-
它在二分类数据集上表现良好;
-
问题是线性可分的。换句话说,它们只能对可以通过直线或超平面将数据分为两类的数据进行分类;
-
本文处理的是一个干净的数据集,几乎没有噪声,这使得感知器能够轻松收敛。
克服这些局限性的一种方法是使用更复杂的模型,如具有非线性激活函数的多层感知器(MLP),MLP可以学习非线性决策边界,从而能够解决更复杂的问题。