KMP 算法 + 详细笔记

news2024/11/30 12:39:42

给两个字符串，T="AAAAAAAAB"，P="AAAAB";

可以暴力匹配，但是太费时和效率不太好。于是KMP问世，我们一起来探究一下吧！！！

（一）最长公共前后缀

D[i] = p[0]~p[i] 区间（前i+1个字母）所拥有的最大......的长度

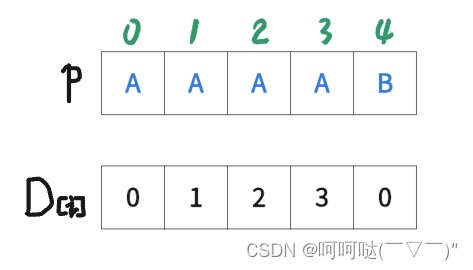
D[0]=0,表示p[0]~p[0]区间（前1个字母）->也就是 A 所拥有的最长公共前后缀长度为0.
D[1]=1,表示p[0]~p[1]区间（前2个字母）->也就是 AA 所拥有的最长公共前后缀长度为1.
D[2]=2,表示p[0]~p[2]区间（前3个字母）->也就是 AAA 所拥有的最长公共前后缀长度为2.
D[3]=3,表示p[0]~p[3]区间（前4个字母）->也就是 AAAA 所拥有的最长公共前后缀长度为3.
D[4]=0,表示p[0]~p[4]区间（前5个字母）->也就是 AAAAB 所拥有的最长公共前后缀长度为0.

我们先手算好了P="AAAAB"的D[i]数组（记录最长公共前后缀），继续挖掘，看看有没有好东西！

（1）举个栗子，T = "AAAAAAAAB"，P="AAAAB" ，D[i]数组上文已经求出

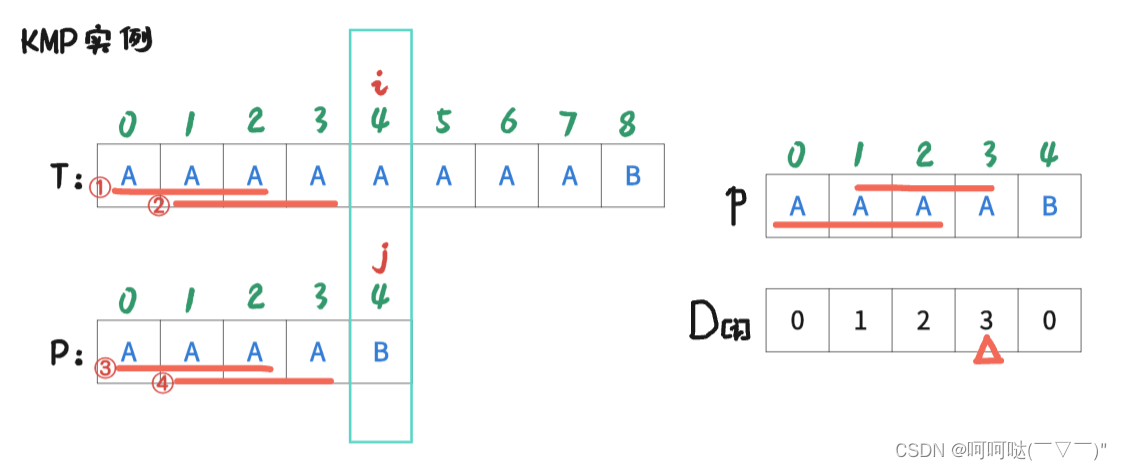
当 i = 4,j = 4 时，T串和 P串发生不匹配，此时我们就发现 T[0-3] 和 P[0-3] 是完全匹配的，那就会思考：是否可以用一些方法来跳过已经判断是能匹配的范围呢？

在 j = 4时，j-1=3，D[3] = 3,也就是意味着P[0]~P[3] 区间（前4个字母）所拥有的最大公共前后缀长度为3.

于是从图中我们可以看到标注为① ② ③ ④ 条红色的线，表示 T 和 P的前后缀相同

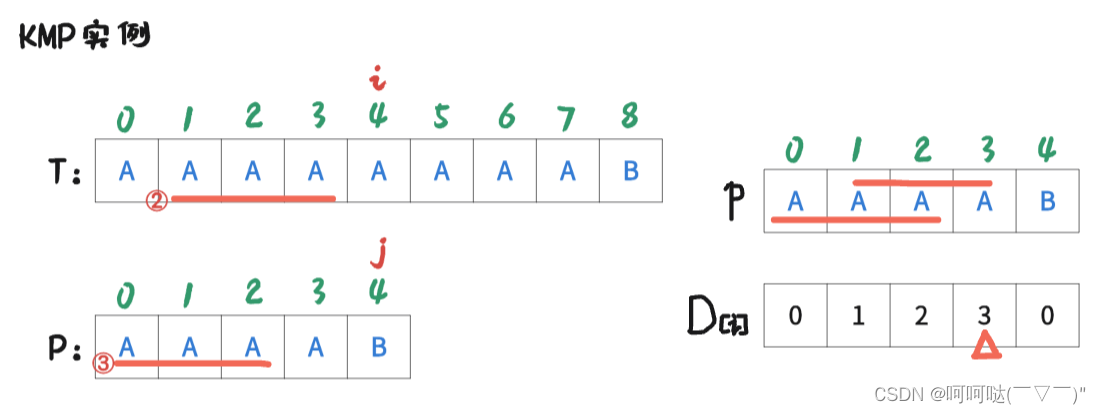着重看②和③这两条，我们可以让 j = 3，即进行操作是：j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。

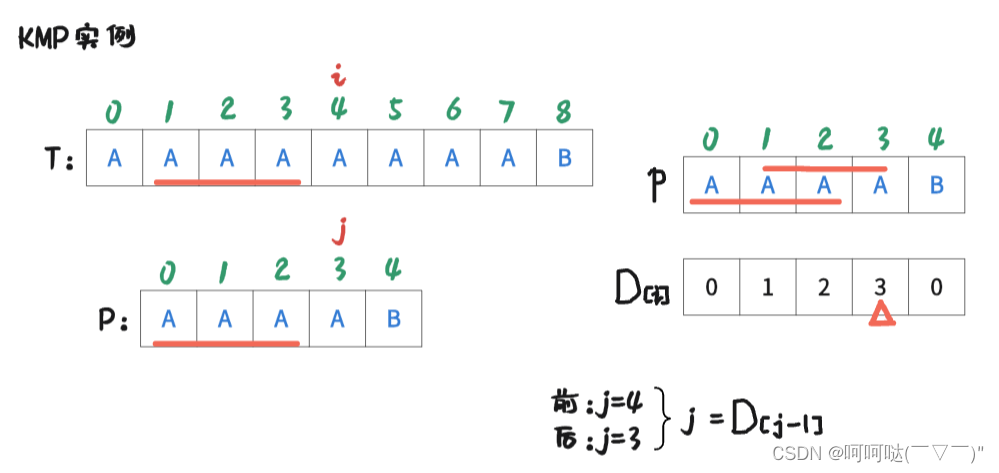
此时 i = 4 , j = 3时，T[4] = P[3],是匹配的，那么让 i++, j++，可得到下图：

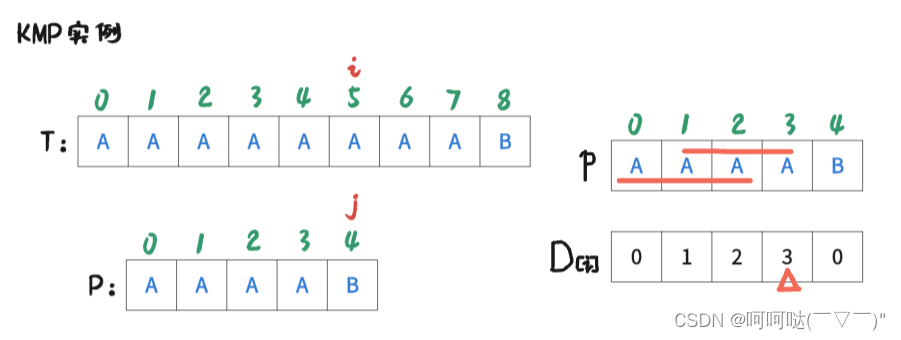
此时 i = 5 , j = 4时，T[5] ≠ P[4],是不匹配的，此时跟前面的操作一样。进行操作是：j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图：

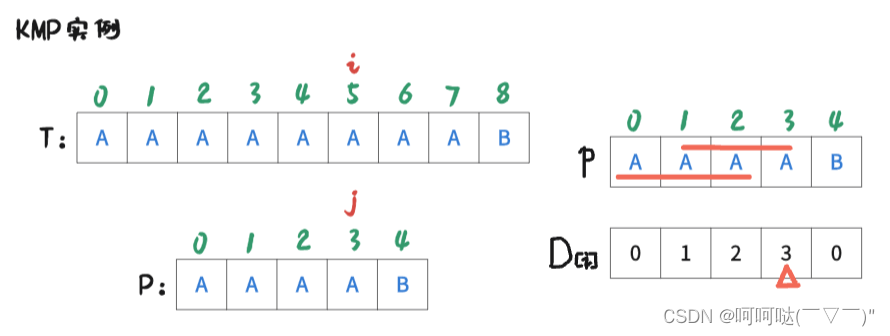
此时 i = 5 , j = 3时，T[5] = P[3],是匹配的，那么让 i++, j++，可得到下图：

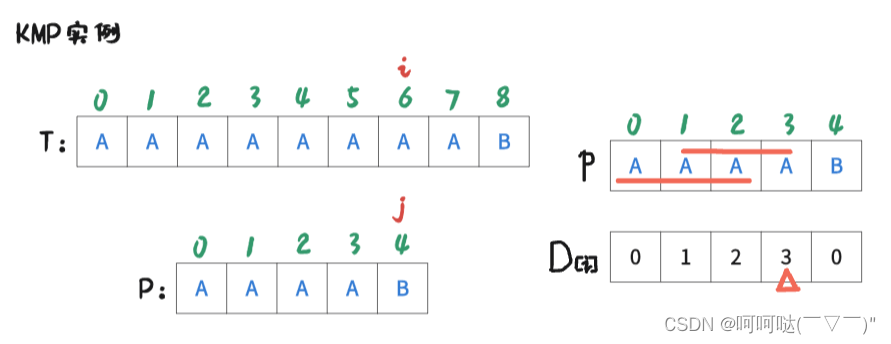
此时 i = 6 , j = 4时，T[6] ≠ P[4],是不匹配的，此时跟前面的操作一样。进行操作是：j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图：

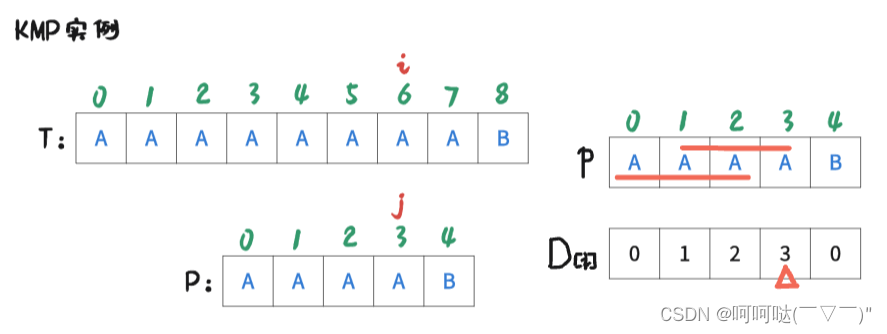
此时 i = 6 , j = 3时，T[6] = P[3],是匹配的，那么让 i++, j++，可得到下图：

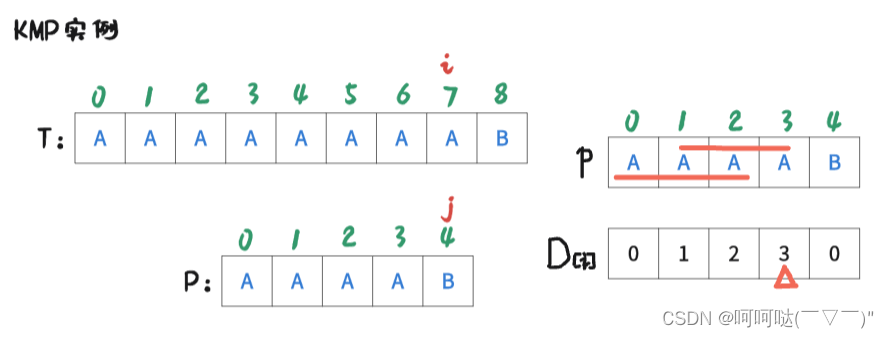
此时 i = 7 , j = 4时，T[7] ≠ P[4],是不匹配的，此时跟前面的操作一样。进行操作是：j = D[4-1]; 再让T[i] 和 P[j] 去判断是否匹配。可得到下图：

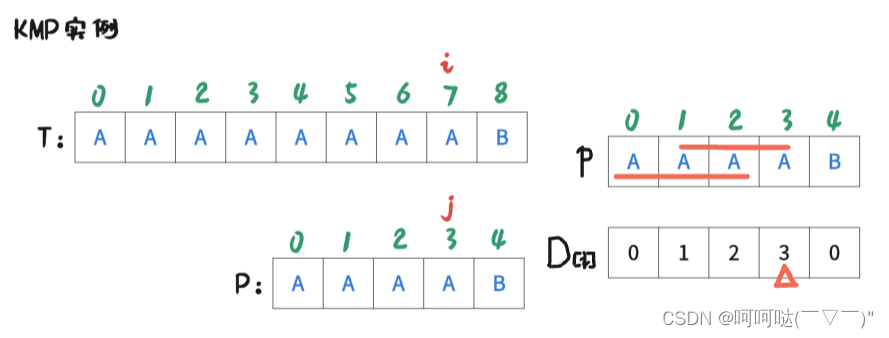
此时 i = 7 , j = 3时，T[7] = P[3],是匹配的，那么让 i++, j++，可得到下图：

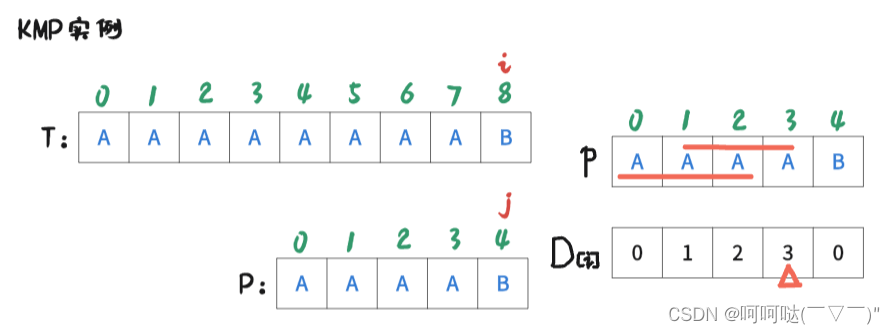
此时 i = 8 , j = 4时，T[8] = P[4],是匹配的，那么让 i++, j++，可得到下图：

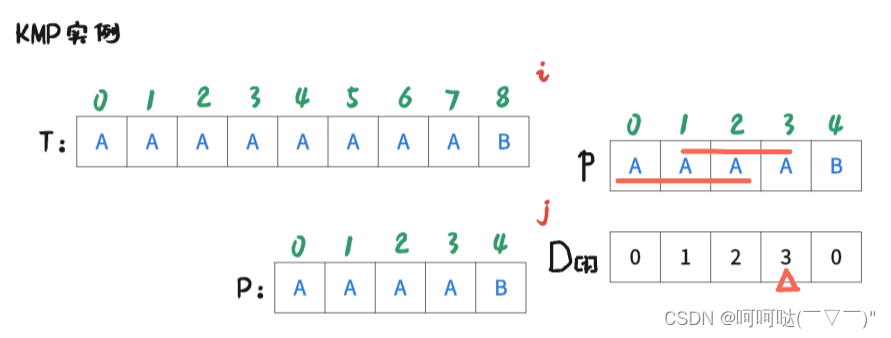
此时 i = 9（越界）, j = 5（越界），终止！

总结：发现已经匹配成功的部分，它所拥有的最大公共前后缀就不用重复进行比较了，不用再花费无效的时间进行比较了，最大公共前后缀越长，那它所省略的就越多，效率也就越高。相对于暴力匹配来说，效率提升也就越高。

kmp核心思路的关键所在：

1.必须理解 D[j] 的意义:P串的前 j+1个字母,即 P[0]~P[j] 所拥有的最大公共前后缀
2.匹配到T[i] != P[j]失败时,想一想P[j]是不是P串的第j+1个字母,是不是也意味着:P[0]~P[j-1]的这前j个字母已经匹配成功了
3.P[0]~P[j-1]的这前 j 个字母的最大公共前后缀 = D[j-1]

----来自B站Up邋遢大王233的评论区回复

（二）KMP Code

D[i] = P[0]至P[i]，P串前 i+1 个字母拥有的最大公共前后缀的长度

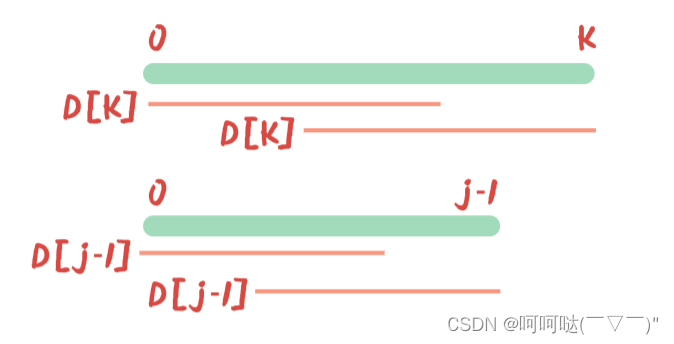
D[k] 表示 P[0]~P[k]时，前 k+1 个 字母拥有的最大公共前后缀的长度

同理，D[j-1]： P[0]~P[j-1]， 前 j 个 字母拥有的最大公共前后缀的长度

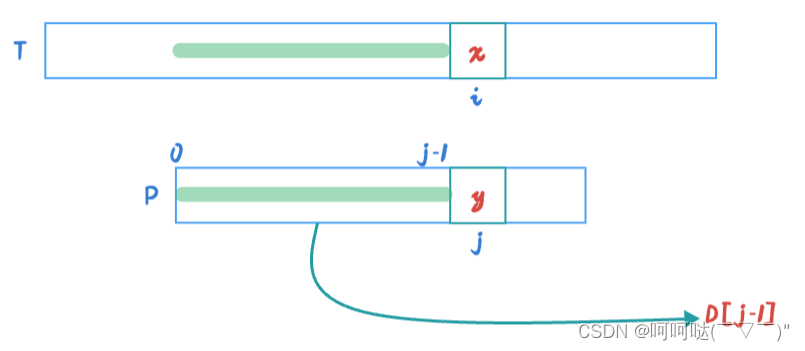
结合上图，D[j-1]：P[0]~P[j-1]，前 j 个 字母拥有的最大公共前后缀的长度

在上图我们知道，在 i 位置的 x 和 j 位置的 y 匹配失败。此时该怎么办呢？为了更好的观察规律，我们不妨设D[j-1] = 3，也就是说P[0]~P[j-1]，前 j 个 字母拥有的最大公共前后缀的长度为3。此时如下图：

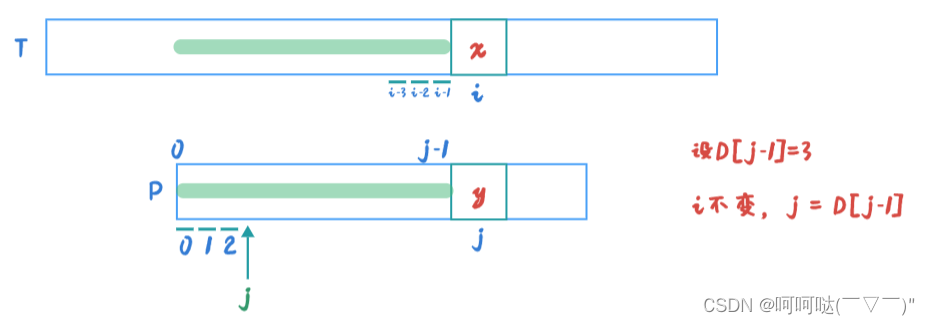
那么让 j = D[j-1] = 3，此时 j 的位置更新到下标为3这个位置，再从j = 3这个位置与 T 串的 x进行匹配判断

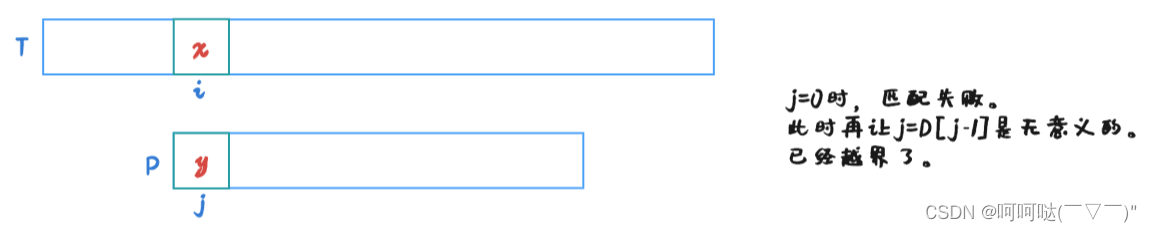
若 j = 0时，匹配失败。此时再让 j = D[j-1]是无意义的。已经越界了。那怎么办呢？

若 j = 0时，匹配失败。让 j 不变，i++

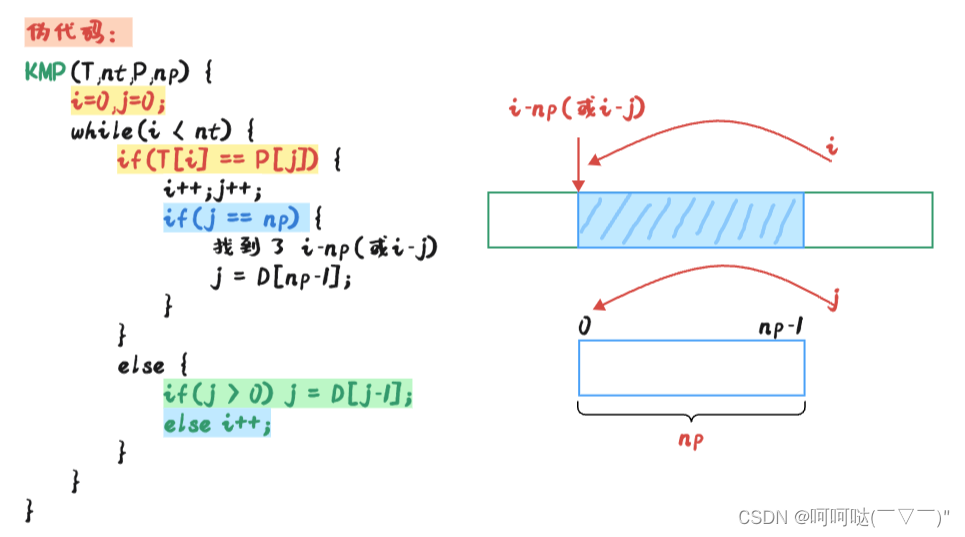j == np (视频中没有介绍后续如何继续匹配，所以一旦匹配成功一次就结束算法了)。而匹配失败时j只可能减少不可能增加第一次匹配成功后，后续想要继续的话，继续 j = D[j-1] 就可以了(此时必然 j = np ,所以写成 j=D[np-1] 也对) ----来自B站Up邋遢大王233的评论区回复