从基础到卷积神经网络（第14天）

news2024/11/19 0:48:53

1. PyTorch 神经网络基础

1.1 模型构造

1. 块和层

首先，回顾一下多层感知机

import torch 
from torch import nn
from torch.nn import functional as F

net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

X = torch.rand(2, 20) # 生成随机输入（批量大小=2， 输入维度=20）
net(X) # 输出（批量大小=2, 输出维度=10）

在这里插入图片描述

2. 自定义块

自定义MLP实现上一节的功能

class MLP(nn.Module): # 定义nn.Mudule的子类
    def __init__(self): 
        super().__init__() # 调用父类
        self.hidden = nn.Linear(20, 256) # 定义隐藏层
        self.out = nn.Linear(256, 10) # 定义输出层
        
    def forward(self, X): # 定义前向函数
        return self.out(F.relu(self.hidden(X))) # X-> hidden-> relu-> out

实例化MLP的层，然后再每次调用正向传播函数时调用这些层

net = MLP()
net(X)

在这里插入图片描述

3. 实现Sequential类

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for block in args:
            self._modules[block] = block
        
    def forward(self, X):
        for block in self._modules.values():
            X = block(X)
        return X

net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
net(X)

在这里插入图片描述

4. 在正向传播中执行代码

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.rand_weight = torch.rand((20, 20), requires_grad=False) # 加入随机权重
        self.linear = nn.Linear(20, 20)

    def forward(self, X):
        X = self.linear(X)
        X = F.relu(torch.mm(X, self.rand_weight) + 1) # 输入和随机权重做矩阵乘法 + 1（偏移）-》激活函数
        X = self.linear(X)
        while X.abs().sum() > 1: # 控制X小于1
            X /= 2
        return X.sum() # 返回一个标量

net = FixedHiddenMLP()
net(X)

5. 混合搭配各种组合块的方法

class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
                                 nn.Linear(64, 32), nn.ReLU())
        self.linear = nn.Linear(32, 16)
    
    def forward(self, X):
        return self.linear(self.net(X)) # 输入-> net-> linear中

chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP()) # (32, 16)->(16, 20) ->(20, 1)
chimera(X)

在这里插入图片描述
总结：
1、在init中写各种层
2、在前向函数中调用init中各种层
有很强的灵活性

1.2 参数构造

具有单隐藏层的MLP

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

在这里插入图片描述
参数访问

print(net[2].state_dict()) # 拿到nn.Linear的相关参数

在这里插入图片描述
访问目标参数

print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)
net[2].weight.grad == None # 梯度是否为0，因为此时还没有计算，所以没有梯度

在这里插入图片描述
一次访问所有参数

print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])

输出没有block1是因为第二层是ReLU是没有参数的
在这里插入图片描述

net.state_dict()['2.bias'].data # 访问最后一层的偏移

在这里插入图片描述
从嵌套块收集参数

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(), 
                         nn.Linear(8, 4), nn.ReLU())

def block2(): # block2嵌套4个block1
    net = nn.Sequential()
    for i in range(4): 
        net.add_module(f'block {i}', block1()) 
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

在这里插入图片描述

print(rgnet) # 查看网络结构

在这里插入图片描述
内置初始化

def init__normal(m): # 传入的module
    if type(m) == nn.Linear: # 如果传入的是全连接层
        nn.init.normal_(m.weight, mean=0, std=0.01) # 内置初始化，均值为0方差为1，.normal_替换函数不返回
        nn.init.zeros_(m.bias) # 所有的bias赋0

net.apply(init__normal) # 对神经网络模型net中的所有参数进行初始化，使用init_normal()函数对参数进行随机初始化
net[0].weight.data[0], net[0].bias.data[0]

在这里插入图片描述

def init_constant(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 1) # 将m.weight初始常数化为1
        nn.init.zeros_(m.bias)

net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]

在这里插入图片描述
不建议权重全部常数化，会导致所有向量向一致的方向发展

对某些块应用不同的初始化方法

def xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight) # 使用Xavier均匀分布进行初始化

def init_42(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 42)

net[0].apply(xavier) # 第一个层用xavier初始化
net[2].apply(init_42) # 第二个层用init_42进行初始化
print(net[0].weight.data[0])
print(net[2].weight.data)

在这里插入图片描述
自定义初始化

def my_init(m):
    if type(m) == nn.Linear:
        print(
            "Init",
            *[(name, param.shape) for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10, 10)
        m.weight.data *= m.weight.data.abs() >= 5 # 对大于等于5的位置进行保留，小于5的位置进行置零操作

net.apply(my_init) # 使用my_init对net进行初始化
net[0].weight[:2]

在这里插入图片描述
直接进行替换

net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]

在这里插入图片描述
参数绑定（在不同的网络之间共享权重的方法）

shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), shared, nn.ReLU(), shared,  # 2和4层共享权重
                    nn.ReLU(), nn.Linear(8, 1))
net(X)
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] =100 # 当共享层中有层参数发生变化时，别的层参数也会发生变化（同步变化）
print(net[2].weight.data[0] == net[4].weight.data[0])

1.3 自定义层

构造一个没有任何参数的自定义层

import torch
import torch.nn.functional as F
from torch import nn

class CenteredLayer(nn.Module): # 层也是nn.Module的子类
    def __init__(self):
        super().__init__()
    
    def forward(self, X):
        return X - X.mean()

layer = CenteredLayer()
layer(torch.FloatTensor([1, 2, 3, 4, 5]))

在这里插入图片描述
将层作为组件合并到构建更复杂的模型

net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())

Y = net(torch.rand(4, 8))
Y.mean() # 不会真等于0是因为存在浮点的误差

带参数的图层

class MyLinear(nn.Module):
    def __init__(self, in_units, units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, units)) # 自定义参数要将其包裹在nn.Parameter中
        self.bias = nn.Parameter(torch.randn(units,))
    
    def forward(self, X):
        linear = torch.matmul(X, self.weight.data) + self.bias.data
        return F.relu(linear)

dense = MyLinear(5, 3) # 输入是5.输出是3
dense.weight

使用自定义层直接执行正向传播计算

dense(torch.rand(2, 5))

使用自定义层构建模型

net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
net(torch.rand(2, 64))

1.4 读写文件

加载和保存张量

import torch 
from torch import nn
from torch.nn import functional as F

x = torch.arange(4) # 构造长为4的向量
torch.save(x, 'x-file') # 把x存在当前文件目录下

x2 = torch.load("x-file") # 从指定的文件路径（"x-file"）加载一个PyTorch模型或张量
x2

存储一个张量列表，然后把它们读回内存

y = torch.zeros(4)
torch.save([x, y], 'x-file')
x2, y2 = torch.load('x-file')
(x2, y2)

在这里插入图片描述
写入或读取从字符串映射到张量的字典

mydict = {'x' : x, 'y' : y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
mydict2

在这里插入图片描述
加载和保存模型参数

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.output = nn.Linear(256, 10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size = (2, 20))
Y = net(X)

将模型的参数（主要是权重）存储到一个叫‘mlp.params’的文件

torch.save(net.state_dict(), 'mlp.params')

实例化了原始多层感知机的一个备份，直接读取文件中存储的参数

clone = MLP()
clone.load_state_dict(torch.load("mlp.params")) # 从指定的文件路径（"mlp.params"）加载一个PyTorch模型的参数，并将这些参数应用到一个新的模型实例（clone）上
clone.eval()

在这里插入图片描述
验证

Y_clone = clone(X)
Y_clone == Y

在这里插入图片描述

使用GPU

查看gpu

!nvidia-smi

查询可用gpu的数量

import torch
from torch import nn

torch.cuda.device_count()

计算设备

import torch
from torch import nn

torch.device('cpu'), torch.cuda.device('cuda')

这两个函数允许我们在请求的GPU不存在的情况下运行代码

def try_gpu(i=0):  
    """如果存在,则返回gpu(i),否则返回cpu()。"""
    if torch.cuda.device_count() >= i + 1:
        return torch.device(f'cuda:{i}')
    return torch.device('cpu')

def try_all_gpus():  
    """返回所有可用的GPU,如果没有GPU,则返回[cpu(),]。"""
    devices = [
        torch.device(f'cuda:{i}') for i in range(torch.cuda.device_count())]
    return devices if devices else [torch.device('cpu')]

try_gpu(), try_gpu(10), try_all_gpus()

查看张量所在的设备，默认是在cpu上

x = torch.tensor([1, 2, 3])
x.device

存储在GPU上

X = torch.ones(2, 3, device=try_gpu())
X
Y = torch.rand(2, 3, device=try_gpu())
Y

计算X+Y，要决定在哪里执行这个操作，如果不在同一个gpu要执行拷贝

Z = X.cuda(0)
Y + Z

神经网络和GPU

net = nn.Sequential(nn.Linear(3, 1))
net = net.to(device=try_gpu()) # 将cpu上创建好的网络挪到gpu上

net(X)

确认模型参数存储在同一个GPU上

net[0].weight.data.device

2. 卷积层

  • 卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
  • 核矩阵和偏移是可学习的参数
  • 核矩阵的大小是超参数

实现：
互相关运算：
【当我们使用 nn.Parameter() 将张量包装成可优化参数时，该参数将被注册到模型的参数列表中，以便在反向传播期间更新和优化。这样，我们可以在定义模型时，使用 nn.Parameter() 创建可训练的权重、偏置等参数，并在训练过程中对其进行优化。

例如，可以使用 nn.Parameter() 创建一个可训练的权重矩阵参数：

weight = nn.Parameter(torch.randn(3, 4))
在模型训练过程中，优化器可以自动更新这个权重参数，以最小化损失函数。】

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):   # X是输入，K是核矩阵
    """计算二维互相关运算。"""
    h, w = K.shape # 行数和列数
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # 输出的行列
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

验证：

# 验证
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
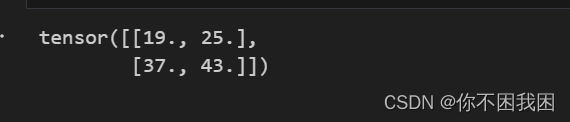
corr2d(X, K)

在这里插入图片描述
实现二维卷积层：

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size)) # 生成一个指定大小kernel_size的随机张量,nn.Parameter张量包装成可优化参数
        self.bias = nn.Parameter(torch.zeros(1)) # 生成一个大小为1的全零张量（标量）
    
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias # 用x和weight做互相关运算再加上偏移

卷积层的一个简单应用：检测图像中不同颜色的边缘

X = torch.ones((6, 8))
X[:, 2:6] = 0
X

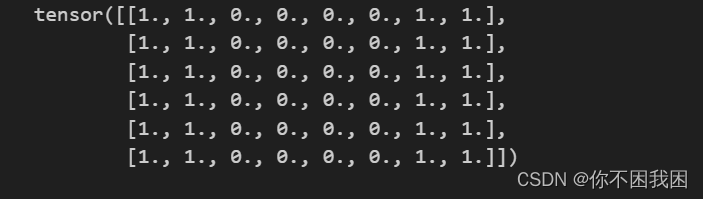
在这里插入图片描述
定义一个卷积核

K = torch.tensor([[1.0, -1.0]]) # 卷积核已知

# 输出Y 中的1代表从白色到黑色的边缘（从1-》0），-1代表从黑色到白色的边缘（从0到-1）
Y = corr2d(X, K)
Y

在这里插入图片描述
缺点：自定义的卷积核K 只能检测垂直边缘

corr2d(X.t(), K) # X.t()对X做转置，X边缘成横向

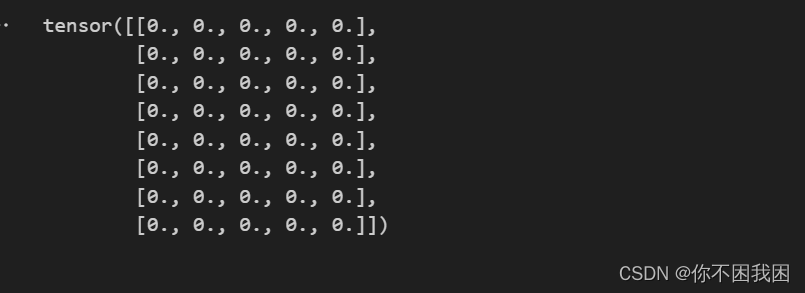
在这里插入图片描述
学习由X生成Y的卷积核：在K未知的情况下，由输入和输出学习出K

conv2d = nn.Conv2d(1, 1, kernel_size = (1, 2), bias=False) # 输入通道= 1， 输出通道= 1

X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))

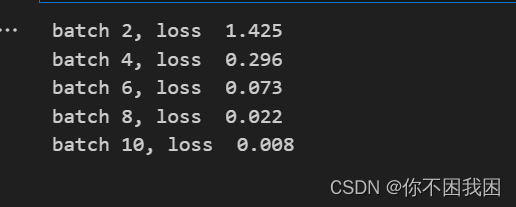
for i in range(10): # 迭代十轮
    Y_hat = conv2d(X)
    l = (Y_hat - Y)**2 # 使用均方误差作为损失
    conv2d.zero_grad() # 把con2d的梯度设为0
    l.sum().backward() # 计算梯度
    conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad # 以3e-2学习率，将卷积层的权重参数更新为当前权重参数减去梯度乘以学习率，[:]原地更新
    if (i + 1) % 2 == 0: #每两轮进行输出
        print(f'batch {i + 1}, loss {l.sum(): .3f}')

在这里插入图片描述
所学的卷积核的权重张量

# 所学的卷积核的权重张量
conv2d.weight.data.reshape((1, 2))

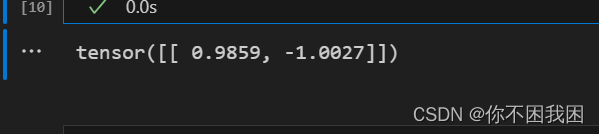
在这里插入图片描述
可以看到经过10论学习后的K 值和最开始自定的（1， -1）非常接近，可以完成由检测X的边缘

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1095348.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

苍穹外卖(七) Spring Task 完成订单状态定时处理

苍穹外卖(七) Spring Task 完成订单状态定时处理

Spring Task 完成订单状态定时处理, 如处理支付超时订单 Spring Task介绍 Spring Task 是Spring框架提供的任务调度工具，可以按照约定的时间自动执行某个代码逻辑。 应用场景: 信用卡每月还款提醒 火车票售票系统处理未支付订单 入职纪念日为用户发送通知 点外…
阅读更多...
C++：多态讲解

C++：多态讲解

多态 1.多态的概念2.多态的定义和实现2.1多态构成条件2.2虚函数2.3虚函数的重写(覆盖)2.4 C11 override 和 final2.5重载、重写(覆盖)、隐藏(重定义)的对比 3.抽象类4.多态的原理5.单继承和多继承关系的虚函数表5.1单继承5.2多继承5.3菱形继承和多态 1.多态的概念 多态的概念&…
阅读更多...
【Vue面试题二十三】、你了解vue的diff算法吗？说说看

【Vue面试题二十三】、你了解vue的diff算法吗？说说看

文章底部有个人公众号：热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享？ 踩过的坑没必要让别人在再踩，自己复盘也能加深记忆。利己利人、所谓双赢。 面试官：你了解vue的diff算法吗&…
阅读更多...
MFC-对话框

MFC-对话框

目录 1、模态和非模态对话框： （1）、对话框的创建 （2）、更改默认的对话框名称 （3）、创建模态对话框 1）、创建按钮跳转的界面 2）、在跳转的窗口添加类 3&#xff0…
阅读更多...
树莓派：64位 RPI OS（Bookworm） 更换国内源

树莓派：64位 RPI OS（Bookworm） 更换国内源

几天前新的RPI OS发布了。官方的发版说明里明确注明已经基于Debian Bookworm了。总的来说切到国内源（清华）跟Bullseye差不多，细节上只有一丢丢不同（non-free变成了non-free-firmware）。 老规矩，仍然是修改…
阅读更多...
二、深度测试（Z Test）

二、深度测试（Z Test）

1.是什么 ①从渲染管线出发 ②书面上理解 所谓深度测试，就是针对当前对象在屏幕上（更准确的说是frame buffer）对应的像素点，讲对象自身的深度值与当前该像素点缓存的深度值进行比较，如果通过了，本对象再改…
阅读更多...
七、三层交换机不同网段通信实验

七、三层交换机不同网段通信实验

拓扑图： 首先将所有端口ip配置完毕，之后对SW1三层交换机进行配置 创建Vlan10 20网段 进入g0/0/1物理端口，只允许vlan10通过 再进入到g0/0/2端口配置允许通过vlan20的数据包 之后进入vlan的虚拟接口去配置网关ip，一定要先配置物理…
阅读更多...
vue:diff库实现文本对比

vue:diff库实现文本对比

官方文档 https://www.npmjs.com/package/diff 安装&#xff1a;npm install diff 内容 <template><div><div style"white-space: pre-line;display: flex;"><div><span class"default">{{oldStr}}</span></div&…
阅读更多...
游游的字母串 （环形数组两点之间的位置）

游游的字母串 （环形数组两点之间的位置）

题目链接&#xff1a;登录—专业IT笔试面试备考平台_牛客网 题目&#xff1a; 样例&#xff1a; 输入 yab 输出 3 思路&#xff1a; 暴力枚举&#xff0c;全部变成对应的26个字母字符需要的操作步数&#xff0c;取最少的一个操作步数&#xff0c; 这里的操作步数&#xff0…
阅读更多...
2021年12月 Python（二级）真题解析#中国电子学会#全国青少年软件编程等级考试

2021年12月 Python（二级）真题解析#中国电子学会#全国青少年软件编程等级考试

Python编程&#xff08;1~6级&#xff09;全部真题・点这里 C/C编程&#xff08;1~8级&#xff09;全部真题・点这里 一、单选题&#xff08;共25题&#xff0c;每题2分&#xff0c;共50分&#xff09; 第1题 执行以下程序 a[33,55,22,77] a.sort() for i in a:print(i)运行…
阅读更多...
Java字符串String

Java字符串String

【char】类型代表字符类型&#xff0c;【String】类型代表字符串类型&#xff1b; 1.String类 1.1 声明字符串 在Java中字符串必须包含在一对双引号&#xff08;“ "&#xff09;之内。双引号包含的都是字符串。 声明字符串语法&#xff1a; String str; //声明字符串语…
阅读更多...
产品经理如何有效跟进开发进度？

产品经理如何有效跟进开发进度？

作为产品经理&#xff0c;很难跟进开发过程。随着软件开发的复杂性和不断变化的产品环境&#xff0c;产品经理必须保持在开发过程的顶端&#xff0c;并确保目标得到满足。产品经理如何跟进开发进度&#xff1f; 第一步是对开发过程本身有一个扎实的理解。产品经理必须熟悉开发过…
阅读更多...
模型预测控制（MPC）中考虑约束中的不确定性（Matlab代码实现）

模型预测控制（MPC）中考虑约束中的不确定性（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
OpenAI开放gpt-3.5turbo微调fine-tuning测试教程

OpenAI开放gpt-3.5turbo微调fine-tuning测试教程

文章目录 openai微调 fine-tuning介绍openai微调地址jsonl格式数据集准备点击上传文件 openai微调 fine-tuning介绍 openai微调地址 网址&#xff1a;https://platform.openai.com/finetune jsonl格式数据集准备 使用Chinese-medical-dialogue-data数据集git clone进行下载 …
阅读更多...
iOS 17请了一个免费的医生！它为你免费预诊断你的焦虑和抑郁

iOS 17请了一个免费的医生！它为你免费预诊断你的焦虑和抑郁

你的iPhone&#xff08;多亏了iOS 17&#xff09;现在有了心理健康问卷&#xff0c;可以帮助诊断焦虑和抑郁&#xff0c;并帮助你了解两者的风险。 心理健康问题通常是可怕的、复杂的和微妙的&#xff0c;你不能总是准确地说出你的感受属于哪一类。因此&#xff0c;如果你正在…
阅读更多...
GB28181学习（八）——历史视音频的回放

GB28181学习（八）——历史视音频的回放

要求 采用SIP协议实现会话&#xff1b;采用SIP扩展协议INFO方法的消息体携带视音频回放控制命令&#xff1b;采用RTP/RTCP实现媒体传输&#xff1b;媒体回放控制命令引用MANSRTSP协议中的PLAY、PAUSE、TEARDOWN的请求消息和应答消息&#xff1b;媒体流接收者可为SIP客户端、SI…
阅读更多...
Windows系统上配置Python开发环境

Windows系统上配置Python开发环境

目录 Python安装程序 运行安装程序 选择安装选项 完成安装 自动环境变量设置 手动环境变量设置 验证安装 Python安装程序 首先&#xff0c;您需要从Python官方网站&#xff08;https://www.python.org/downloads/&#xff09;下载Python的最新稳定版本。在页面上选择适用…
阅读更多...
接口自动化测试_L3

接口自动化测试_L3

目录&#xff1a; 整体结构响应断言 响应信息数据极为庞大&#xff0c;针对于“大响应数据”如何断言JSONSchema 简介JSONSchema 整体结构响应断言JSONSchema 的生成JSONSchema 的生成效果界面工具生成第三方库生成&#xff08;Python&#xff09;JSONSchema 验证&#xff08;…
阅读更多...
scratch躲避陨石 2023年9月电子学会图形化编程scratch编程等级考试三级真题和答案解析

scratch躲避陨石 2023年9月电子学会图形化编程scratch编程等级考试三级真题和答案解析

目录 scratch躲避陨石 一、题目要求 1、准备工作 2、功能实现 二、案例分析
阅读更多...
【java学习—七】多态性（34）

【java学习—七】多态性（34）

文章目录 1. 概念2. 对象的多态2.1. 一2.2. 二 3. 虚拟方法的调用4. 总结 1. 概念 多态性&#xff0c;是面向对象中最重要的概念&#xff0c;在 java 中有两种体现&#xff1a; &#xff08;1&#xff09;方法的重载 (overload) 和重写 (overwrite) 。 重载&#xff1a;本类中…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023