## 题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B$点 (n, m)，同样马的位置坐标是需要给出的。

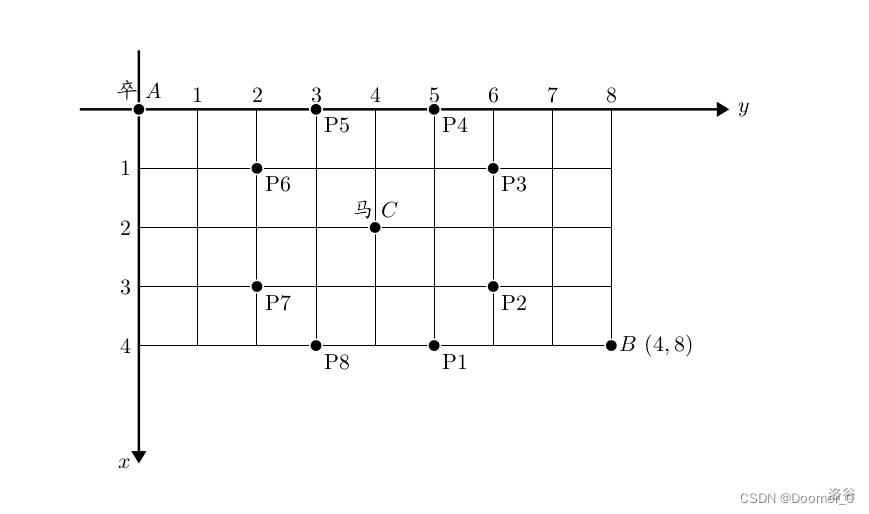
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

## 输入格式

一行四个正整数，分别表示 B 坐标和马的坐标。

## 输出格式

一个整数，表示所有的路径条数。

## 样例 #1

### 样例输入 #1
6 6 3 3

### 样例输出 #1
6

## 提示

对于 100 % 的数据，1≤n,m≤20，0≤ 马的坐标 ≤20。

分析：

首先要先考虑递推式，并且考虑终止条件

我们对于要到达的b（xb，yb）点，设置一个f（x，y），表示从0，0走到f点的可能数

对于任意的一个点，如果想到达本点，只能从左方和上方移动过来

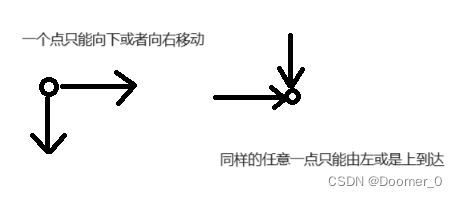
本点坐标如果为x，y则左边点坐标为（x-1,y）上边点坐标为（x,y-1）,如果说从左边到本点的可能性为a，从上边到本点的可能性为b，则到达本点总可能性为a+b

因此我们可以得出递推式：f(x,y)=f(x-1,y)+f(x,y-1)

终止条件：

首先第一个点（0，0）到达这个点的可能次数只有1，而（0，y）（x，0）这两条边界的点到达可能同样也只有一种，最后是马以及马脚所在的点，到达的可能性一定为0。

分析完毕，思考解题思路，首先对数据进行输入，用二维数据来模拟棋盘，如果不能走就赋值为1，反之为0。再设置一个二维数组来对f函数即可能到达的可能性进行记录，像是边界直接给赋值1，之后利用递推式依次递推到B点就可以了

一、输入

这边有一个问题，就是如果我的马在1行或者存在于1列，必然会导致，马脚超出数组范围，我们可以建立保护层来方式超出，就是将每个点都+2使得整体往右下偏移，这样最远的马脚也只能到达0行0列，不会超出。

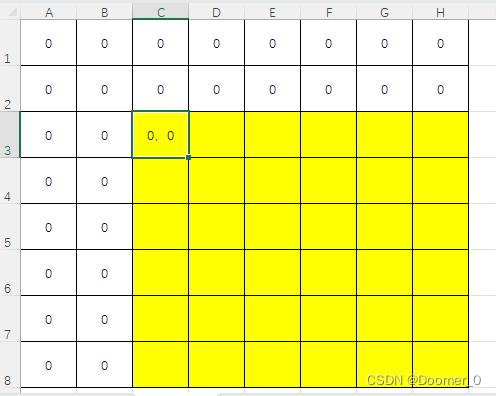
开始定义 马点，B点，以及棋盘和对应点的可能

long long xb,yb,xh,yh;
long long pand[30][30]={0},f[30][30]={0};

依次输入之后做偏移

    cin>>xb>>yb>>xh>>yh;
	xb += 2; yb += 2;
	xh += 2; yh += 2;

二、对边界进行赋值

边界到达的可能只有1，所以可以直接赋值

for(int i=2;i<30;i++){
	f[2][i] = 1;
	f[i][2] = 1;
}

 三、马对应的特殊点进行赋值

在地图上的我们对不能到达也就是可能性为0的点进行标注

    pand[xh][yh] = 1;
	pand[xh-2][yh-1] = 1;
	pand[xh-1][yh-2] = 1;
	pand[xh+2][yh+1] = 1;
	pand[xh+1][yh+2] = 1;
	pand[xh+2][yh-1] = 1;
	pand[xh+1][yh-2] = 1;
	pand[xh-2][yh+1] = 1;
	pand[xh-1][yh+2] = 1;

四、递推的计算f（x,y）

 在这里通过递推式会遇到问题是0，0点也是现如今的2，2点，因为前面的两点的f函数都为0所以将f1，2或者f2，1赋值为1即可

之后通过递推公式，依次判断，如果遇到马或者马脚，就将可能性为0，代表此路不通直接continue

    f[1][2] = 1;
	for(int i = 2;i<=xb;i++){
		for(int j = 2;j<=yb;j++){
			if(pand[i][j]==1){
				f[i][j] = 0;
				continue;
			}
			f[i][j]= f[i-1][j]+f[i][j-1];
		}
	}

五、输出

 直接将f函数可能性输出即可;

完整代码：

#include <bits/stdc++.h>
using namespace std;
long long xb,yb,xh,yh;
long long pand[30][30]={0},f[30][30]={0};
int main(){
	cin>>xb>>yb>>xh>>yh;
	xb += 2; yb += 2;
	xh += 2; yh += 2;
	
	for(int i=2;i<30;i++){
		f[2][i] = 1;
		f[i][2] = 1;
	}
	
	pand[xh][yh] = 1;
	pand[xh-2][yh-1] = 1;
	pand[xh-1][yh-2] = 1;
	pand[xh+2][yh+1] = 1;
	pand[xh+1][yh+2] = 1;
	pand[xh+2][yh-1] = 1;
	pand[xh+1][yh-2] = 1;
	pand[xh-2][yh+1] = 1;
	pand[xh-1][yh+2] = 1;
	
	f[1][2] = 1;
	for(int i = 2;i<=xb;i++){
		for(int j = 2;j<=yb;j++){
			if(pand[i][j]==1){
				f[i][j] = 0;
				continue;
			}
			f[i][j]= f[i-1][j]+f[i][j-1];
		}
	}
	
	cout<<f[xb][yb];
	return 0;
}