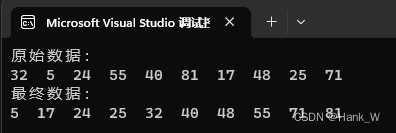
快速排序
算法思想

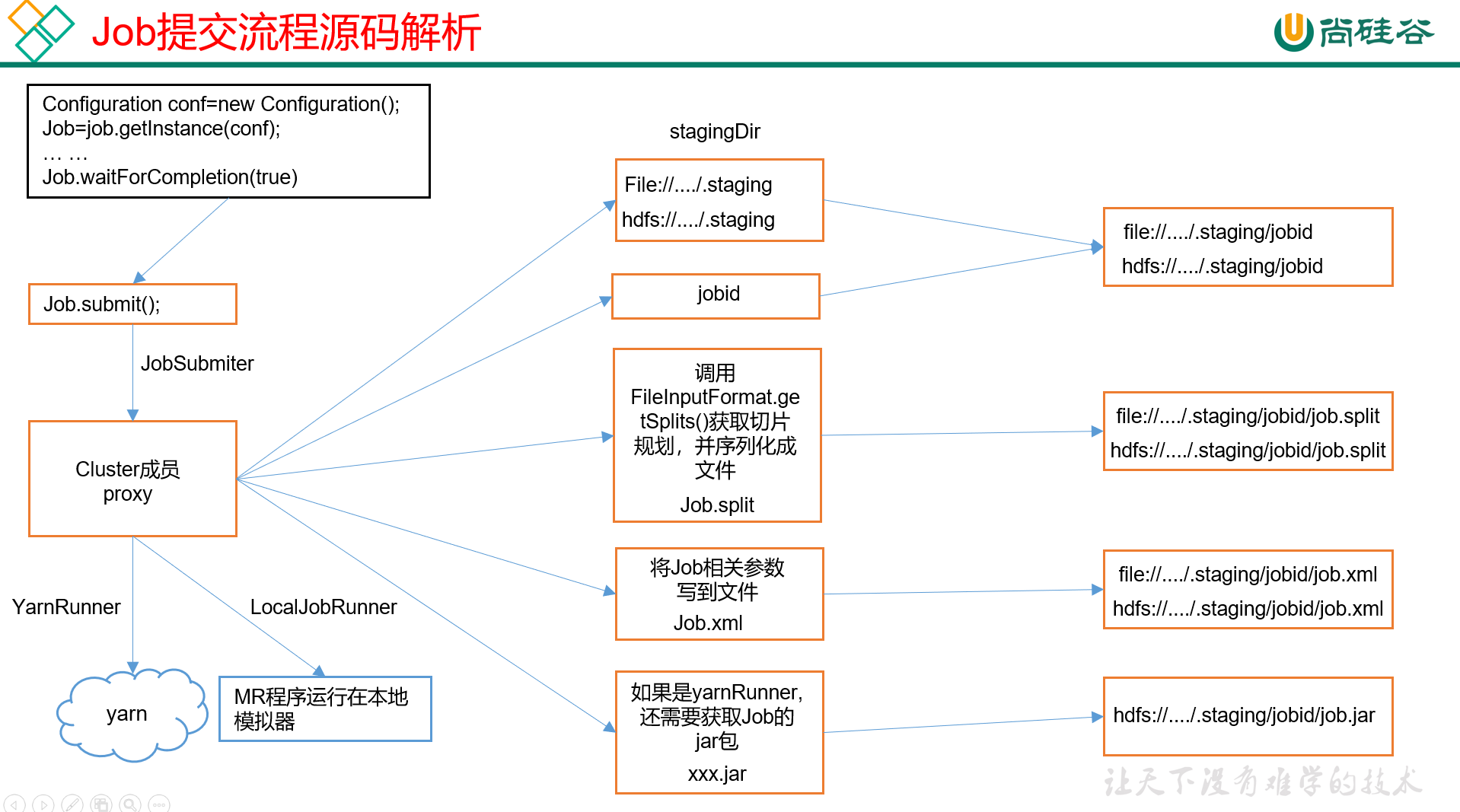
图 1-1
即确定一个基准值(一般为数组中间位置的元素,或者自定义),让待排序数组中所有比基准值小的元素放到基准值左边的位置,所有比基准值大的元素放到基准值右边的位置,这样一趟排序下来,基准值左边的元素都比基准值小,基准值右边的元素都会被基准值大,然后在分别对基准值左右两边的数据进行上述操作,最后得到一个有序数组。
快速排序示意图

图 1-2
代码实现
def quick_sort(arr: list, left: int, right: int):
l = left # 数组左边的下标
r = right # 数组右边的下标
# 基准值,此处取数组中间位置的元素
pivot = arr[(l + r) // 2]
while l < r:
# 从数组最左边开始,寻找比基准值大或等于基准值的元素
# 找到则退出循环,此时 l 位置的元素就是比基准值大的元素
while arr[l] < pivot:
l += 1
# 从数组最右边开始,寻找比基准值小或等于基准值的元素
# 找到则退出循环,此时 r 位置的元素就是比基准值小的元素
while arr[r] > pivot:
r -= 1
# 说明数组中的元素已经以基准值为分界点划分为两部分:比基准值大的在一边,小的在另一边
# 退出循环,在下一次循环时对基准值左边/右边的数组再以新的基准值进行划分
# 直到整个数组有序
if l >= r:
break
# 把上述找到的两个元素交换
# 即把比基准值大的元素放到基准值右边,比基准值小的放在基准值左边
t = arr[l]
arr[l] = arr[r]
arr[r] = t
# 如果 l == r ,要分别加1 和 减1,否则会在 while l < r 处进入死循环
if l == r:
l += 1
r -= 1
if left < r: # 对基准值左边的数据进行递归,重复上述步骤
quick_sort(arr, left, r)
if l < right: # 对基准值右边的数据进行递归,重复上述步骤
quick_sort(arr, l, right)
arr = [-9, 78, 0, 23, -567, 70]
quick_sort(arr, 0, len(arr) - 1)
print(arr) # [-567, -9, 0, 23, 70, 78]归并排序
算法思想

图 2-1

图 2-2
数据的每一次合并过程都是将两个已经有序的数组合并成一个有序数组,遵从相关算法,图2-2的最后一轮合并(第七次合并)如下图:
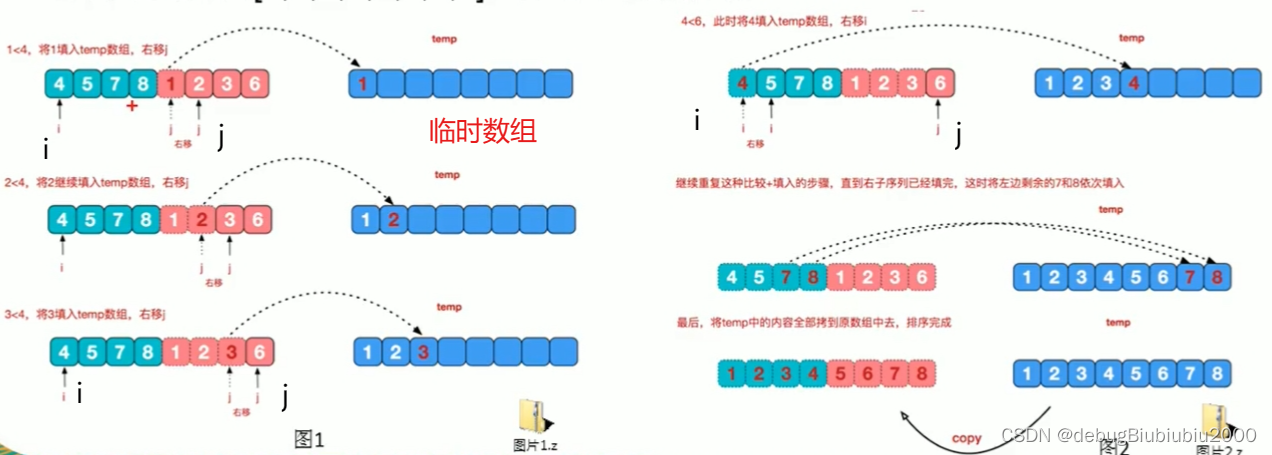
图 2-3
代码实现
def merge(arr: list, left: int, mid: int, right: int):
"""
归并排序的合并部分,本质就是将两个有序数组合并为一个有序数组
现假设两个有序数组分别为数组A和数组B,这两个有序数组都放在数组arr中,以mid位置为分割,mid是数组A的最后一个元素的位置
数组A是图2-3中蓝绿色部分,数组B就是图2-3的粉色部分
:param arr: 待排序数组,包含两个待合并的有序数组,两个有序数组以mid为分割点,数组A是arr的左边部分,数组B是arr右边部分,mid也是数组A的最后一个元素的位置
:param left: 数组A的第一个元素的下标
:param mid: 数组A和数组B起始都是待排序数组中的一部分,mid表示数组A和数组B的中间位置,也就是数组A的最后一个元素
:param right: 数组B的最后一个元素的下标
:return:
如待排序数组为:[8,4,5,7,1,3,6,2],最后将他们分割为八个数组:8,4,5,7,1,3,6,2
1、然后将这八个数组两两合并:8和4,5和7,1和3,6和2,得到四个数组
第一次合并:合并8和4,所以 arr=[8,4,5,7,1,3,6,2], left=0, mid=0, right=1,
数组A=[8], 数组B=[4], 将A和B元素按大小放入temp数组, temp最终结果为:[4,8]
将temp复制到arr中,arr最终为:[4,8,5,7,1,3,6,2]
同理:
第二次合并:合并5和7,所以 arr=[4,8,5,7,1,3,6,2], left=2, mid=2, right=3,
数组A=[5], 数组B=[7], 将A和B元素按大小放入temp数组, temp最终结果为:[5,7]
将temp复制到arr中,arr最终为:[4,8,5,7,1,3,6,2]
第三次合并:合并1和3,所以 arr=[4,8,5,7,1,3,6,2], left=4, mid=4, right=5,
数组A=[1], 数组B=[3], 将A和B元素按大小放入temp数组, temp最终结果为:[1,3]
将temp复制到arr中,arr最终为:[4,8,5,7,1,3,6,2]
第四次合并:合并6和2,所以 arr=[4,8,5,7,1,3,6,2], left=6, mid=6, right=7,
数组A=[6], 数组B=[2], 将A和B元素按大小放入temp数组, temp最终结果为:[2,6]
将temp复制到arr中,arr最终为:[4,8,5,7,1,3,2,6]
2、接下来再把四个数组:[4,8]和[5,7], [1,3]和[2,6]再两两合并,得到两个数组
第五次合并:合并[4,8]和[5,7],所以 arr=[4,8,5,7,1,3,2,6], left=0, mid=1, right=3,
数组A=[4,8], 数组B=[5,7], 将A和B元素按大小放入temp数组, temp最终结果为:[4,5,7,8]
将temp复制到arr中,arr最终为:[4,5,7,8,1,3,2,6]
第六次合并:合并[1,3]和[2,6],所以 arr=[4,5,7,8,1,3,2,6], left=4, mid=5, right=7,
数组A=[1,3], 数组B=[2,6], 将A和B元素按大小放入temp数组, temp最终结果为:[1,2,3,6]
将temp复制到arr中,arr最终为:[4,5,7,8,1,2,3,6]
3、最后把两个数组:[4,5,7,8]和[1,2,3,6]合并为一个数组,得到归并排序的最终结果
第七次合并:合并[4,5,7,8]和[1,2,3,6],所以 arr=[4,5,7,8,1,2,3,6], left=0, mid=3, right=7,
数组A=[4,5,7,8], 数组B=[1,2,3,6], 将A和B元素按大小放入temp数组, temp最终结果为:[1,2,3,4,5,6,7,8]
将temp复制到arr中,arr最终为:[1,2,3,4,5,6,7,8]
"""
i = left # 指向数组A的第一个元素位置
j = mid + 1 # 指向数组B的第一个元素位置
temp = [] # 临时保存元素的中转数组
# t = 0 # 指向中转数组最后一个元素的位置(中转数组初始为空)
# 依次遍历数组A和数组B,将两个数组中较小的元素依次放入中转数组temp(此处按从小到大排序)
# 直到两个数组中有一个遍历完毕,则退出循环
while (i <= mid and j <= right):
if arr[i] <= arr[j]: # 数组A中 i 位置的元素比数组B中 j 位置的元素要小,所以小的放入中转数组
temp.append(arr[i])
i += 1
else: # 反之,数组B中 j 位置的元素比数组A中 i 位置的元素要小,所以小的放入中转数组
temp.append(arr[j])
j += 1
# 退出循环说明有一个数组遍历结束,将另一个没遍历结束的数组的剩余元素全部添加到中转数组temp中
while i <= mid: # 说明先结束的是数组B,将数组A剩余元素添加到中转数组temp
temp.append(arr[i])
i += 1
while j <= right: # 说明先结束的是数组A,将数组B剩余元素添加到中转数组temp
temp.append(arr[j])
j += 1
# 将中转数组temp的元素拷贝到数组arr
t = 0
left_temp = left
while left_temp <= right:
arr[left_temp] = temp[t]
left_temp += 1
t += 1
def merge_sort(arr: list, left: int, right: int):
"""
归并排序的分组及合并部分
:param arr: 待排序的数组
:param left: 已拆分数组的起始位置
:param right: 已拆分数组的最后位置
:return:
"""
if left < right:
mid = (left + right) // 2
merge_sort(arr, left, mid) # 向左递归
merge_sort(arr, mid + 1, right) # 向右递归
merge(arr,left, mid, right) # 合并
sort_arr = [8, 4, 5, 7, 1, 3, 6, 2]
merge_sort(sort_arr, 0, len(sort_arr) - 1)
print(sort_arr)基数排序

图 3-1

图 3-2
算法思想

图 3-3
代码实现
详细步骤代码
def radix_sort_detail(arr: list):
# 假设 arr=[53,3,542,748,14,214]
# 定义一个二维数组bucket[][],二维数组中的第一维bucket[]表示一个桶,即每个桶是一个一维数组
# 因为有0-9十个数字,所以有十个桶,即二维数组的长度为 10
# 每个桶从0开始编号,即名字依次为 0-9
# 其中每一个桶用来存储待排序的元素
# 因为极端情况下可能每个待排序的元素的位数数字一样(如所有待排序元素的个位数都是0),
# 所以每个桶的空间都需要和待排序数组长度一样
# 由此可见基数排序是典型的以空间换时间
bucket = []
# 构造一个具有10行的二维数组
for i in range(10):
bucket.append([])
# 假设 arr=[53,3,542,748,14,214]
############### 第一轮排序:根据待排序数组元素的个位数进行 ###############
# 遍历待排序数组,得到每个元素的个位数,根据个位数对应的数字将该元素放入对应的桶中
# 如某个元素的个位数是0,则将该元素放入0号桶,如果是2,则放入2号桶
for item in arr:
digit = item % 10 # 获取元素的个位数
# 根据个位数的值,将元素放入到对应的桶中
bucket[digit].append(item)
# 将所有元素放入到对应的桶中后
# 从第0个桶开始,依次获取每个桶中的所有元素,将元素放入到arr中
idx = 0
for i in range(len(bucket)): # i为:0-9
if len(bucket[i]) != 0: # 如果桶中有元素,则遍历该桶获取桶中的每一个元素
for item in bucket[i]:
arr[idx] = item
idx += 1
# 每一轮排序过后,把桶清空
bucket[i].clear()
print('第一轮:', arr)
############### 第二轮排序:根据待排序数组元素的十位数进行 ###############
# 遍历待排序数组,得到每个元素的十位数,根据十位数对应的数字将该元素放入对应的桶中
# 如某个元素的十位数是0,则将该元素放入0号桶,如果是2,则放入2号桶
for item in arr:
digit = item // 10 % 10 # 获取元素的十位数
# 根据百位数的值,将元素放入到对应的桶中
bucket[digit].append(item)
# 将所有元素放入到对应的桶中后
# 从第0个桶开始,依次获取每个桶中的所有元素,将元素放入到arr中
idx = 0
for i in range(len(bucket)): # i为:0-9
if len(bucket[i]) != 0: # 如果桶中有元素,则遍历该桶获取桶中的每一个元素
for item in bucket[i]:
arr[idx] = item
idx += 1
# 每一轮排序过后,把桶清空
bucket[i].clear()
print('第二轮:', arr)
############### 第三轮排序:根据待排序数组元素的百位数进行 ###############
# 遍历待排序数组,得到每个元素的百位数,根据百位数对应的数字将该元素放入对应的桶中
# 如某个元素的百位数是0,则将该元素放入0号桶,如果是2,则放入2号桶
for item in arr:
digit = item // 100 % 10 # 获取元素的百位数
# 根据百位数的值,将元素放入到对应的桶中
bucket[digit].append(item)
# 将所有元素放入到对应的桶中后
# 从第0个桶开始,依次获取每个桶中的所有元素,将元素放入到arr中
idx = 0
for i in range(len(bucket)): # i为:0-9
if len(bucket[i]) != 0: # 如果桶中有元素,则遍历该桶获取桶中的每一个元素
for item in bucket[i]:
arr[idx] = item
idx += 1
# 每一轮排序过后,把桶清空
bucket[i].clear()
print('第三轮:', arr)
arr = [53, 3, 542, 748, 14, 214]
radix_sort_detail(arr)
print(arr)完整代码
def radix_sort(arr: list):
# 假设 arr=[53,3,542,748,14,214]
# 定义一个二维数组bucket[][],二维数组中的第一维bucket[]表示一个桶,即每个桶是一个一维数组
# 因为有0-9十个数字,所以有十个桶,即二维数组的长度为 10
# 每个桶从0开始编号,即名字依次为 0-9
# 其中每一个桶用来存储待排序的元素
# 因为极端情况下可能每个待排序的元素的位数数字一样(如所有待排序元素的个位数都是0),
# 所以每个桶的空间都需要和待排序数组长度一样
# 由此可见基数排序是典型的以空间换时间
bucket = []
# 构造一个具有10行的二维数组
for i in range(10):
bucket.append([])
# 获取待排序数组中的最大的数,然后获取最大数是几位数
# 几位数决定了需要排序多少趟
max = 0
for item in arr:
if max < item:
max = item
# 获取一个数是几位数的技巧:将数转换成字符串然后求其长度
count = len(str(max))
num = 0
n = 1 # 表示正在获取的位数(个位数、十位数、百位数...)
while num < count:
# 遍历待排序数组,得到每个元素的每一位数digit,根据digit对应的数字将该元素放入对应的桶中
# 如digit=0,则将该元素放入0号桶,如果是2,则放入2号桶
for item in arr:
digit = item // n % 10 # 依次获取获取元素的个位数、十位数、百位数...
# 根据digit的值,将元素放入到对应的桶中
bucket[digit].append(item)
# 将所有元素放入到对应的桶中后
# 从第0个桶开始,依次获取每个桶中的所有元素,将元素放入到arr中
idx = 0
for i in range(len(bucket)): # i为:0-9
if len(bucket[i]) != 0: # 如果桶中有元素,则遍历该桶获取桶中的每一个元素
for item in bucket[i]:
arr[idx] = item
idx += 1
# 读取桶中的所有元素后,把桶清空
bucket[i].clear()
# 从个位数开始,依次向更高位取值
num += 1
n *= 10
arr = [53, 3, 542,2014, 748, 1451, 214, 100]
radix_sort(arr)
print(arr)