《树与二叉树》

• 二叉树的顺序存储结构

• 顺序存储只适用于完全二叉树和满二叉树，一般二叉树不适用
• i =2 的左孩子为 2i =4，右孩子为 2i +1 =5
  

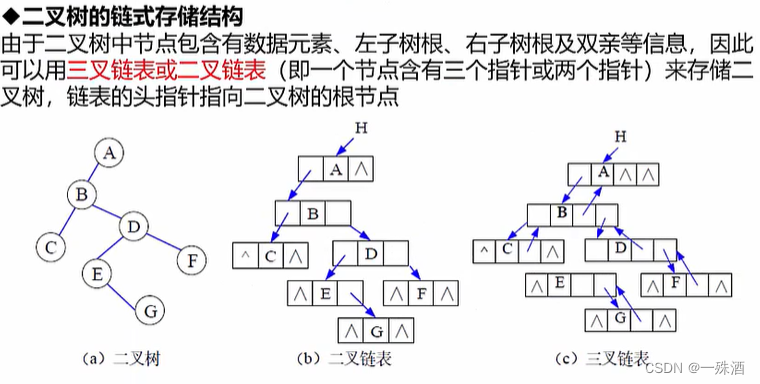
• 二叉树的链式存储结构

• 链式存储适用于二叉树；空结点用“∧”表示
• 二叉链表：左孩子，右孩子
• 三叉链表：左孩子，双亲结点，右孩子
  

• 二叉树的遍历

• 先序（前序）遍历：根，左，右
• 中序遍历：左，根，右
• 后序遍历：左，右，根
• 层次遍历：从上到下，从左到右
  

• 深度为k的二叉树（满二叉树）至多有 (2^k) -1 个节点
• 顺序存储：完全二叉树，一般二叉树需补虚节点——> 2^4 -1 = 15
• 三叉链表：每个节点有3个指针域；——> 1+2+1+0+2+2=8
  

• 线索二叉树

• 保存二叉树遍历时某节点的前驱节点和后继节点的信息
• n个节点的二叉树使用链表存储，则有 n+1 哥空指针域
  

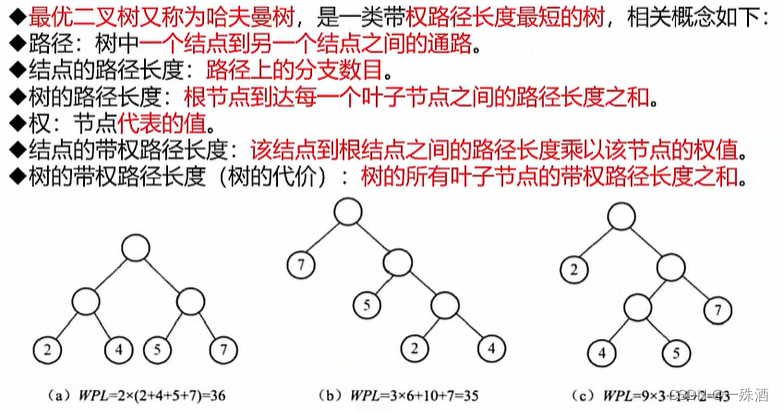
• 哈夫曼树（最优二叉树）

• 带权路径长度最短的树
• 树的路径长度：根节点到每一个叶子节点的路径长度之和
• 树的带权路径长度：树的所有叶子节点的带权路径长度之和
  

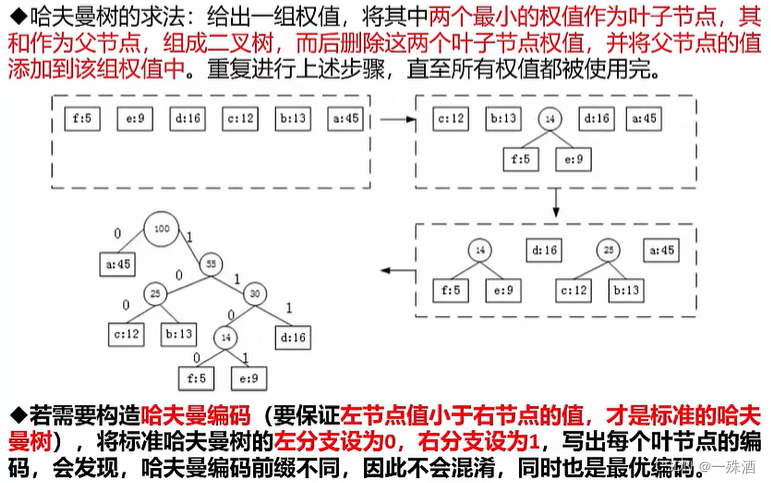
• 哈夫曼树的求法：
• 最小权值为叶子节点，其和为父节点，后删除叶子节点，不断循环，直到所有权值用完
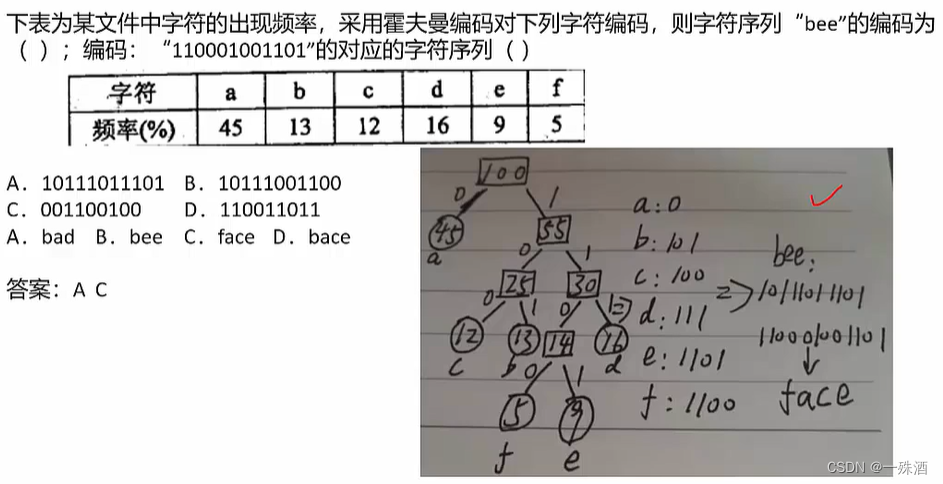
• 哈夫曼树编码：左节点值小于右节点值；左分支设为0，右分支设为1
  

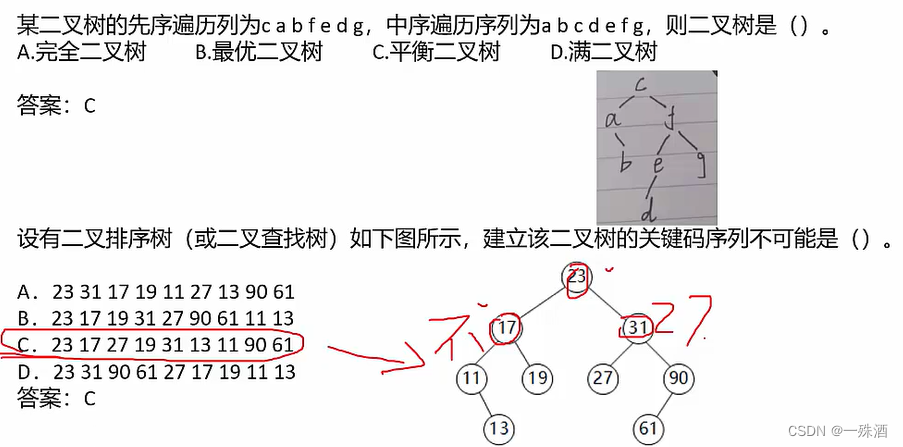
• 查找二叉树（排序二叉树）

• 每个节点的所有左孩子节点值都小于父节点值，而右孩子则大于（左 < 根 < 右）
• 每次查找范围缩小一半，查找效率较高
• 深度越大，效率越低
  
  

• 单枝树：深度最大，效率最低
• 平衡二叉树（AVL树）：深度最小，效率最高；左子树和右子树的高度之差的绝对值不超过1；
  
  

• 二叉树遍历列速解

已知（先序 / 后序） 与中序，求（后序 / 先序）