一、概述
Jenkins 与 Git 的结合使用,可以理解为是 Jenkins 的一个强大之处。为什么要这么说,简要说明一下这个工作模式就能理解: 一个软件项目,开发过程中通常都会使用到一些源码管理工具,来达到团队协作的目的。而 Jenkins 所能实现的功能是,待开发人员将代码提交到源码管理工具中,通过提前设计好的 Jenkins 构建策略等,可以实现一键测试、部署等等。开发人员所要做的就是提交代码至仓库,其余的工作可以交给 Jenkins 完成。
同时,我也为大家准备了一份软件测试视频教程(含面试、接口、自动化、性能测试等),就在下方,需要的可以直接去观看,也可以直接点击文末小卡片免费领取资料文档
软件测试视频教程观看处:
自动化测试篇—实战案例:自动化及接口自动化本质及适用场景
二、具体操作
准备工作:
1、部署 Jenkins 的主机上要安装 Git,安装成功后,可以通过whereis命令获取到 Git 的安装路径。
2、准备好另外一个服务器,Jenkins 将通过节点方式对其实现远程操作。(只使用部署了 Jenkins 这一个服务器进行这个示例也是可行的,即这个服务器即部署了 Jenkins 也“承担”部署软件项目)
3、一个远程的源码仓库。GitHub、GitLab、Gitee 等均可。
4、上传一个 HTML 文件到这个远程仓库(上传至master分支即可)
一个远程的源码仓库并上传一个 HTML 文件
5、在远程服务器中安装好并开启 Tomcat,将通过 Jenkins 将这个 HTML 文件部署至远程服务器的 Tomcat 中。
流程:
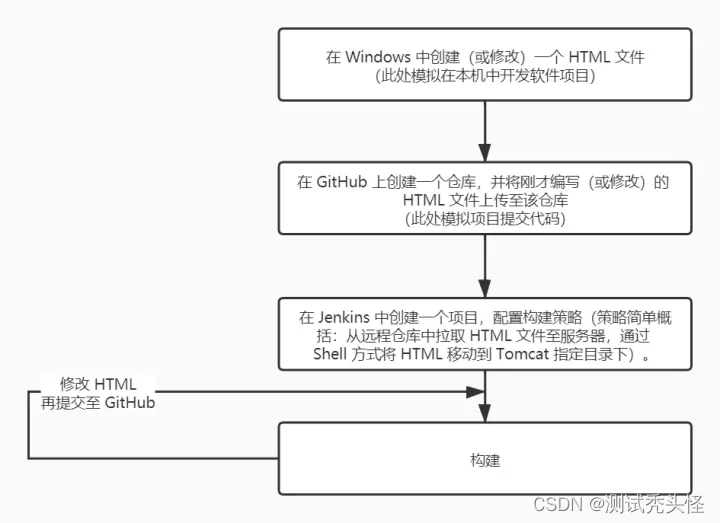
流程
注意:上述的操作仅是简单示例,可能会有不合适的地方。
1、通过whereis命令在部署了 Jenkins 的服务器上获取到 Git 的安装路径。在 Jenkins 主页(首页)点击左侧的“系统管理”,再点击“全局工具配置”,进入“全局工具配置”页面:

全局工具配置
2、填写有关 Git 的配置:Name自定义;Path to Git executable为git命令的路径,可以通过whereis git命令得到;“自动安装”不要勾选。配置后保存。
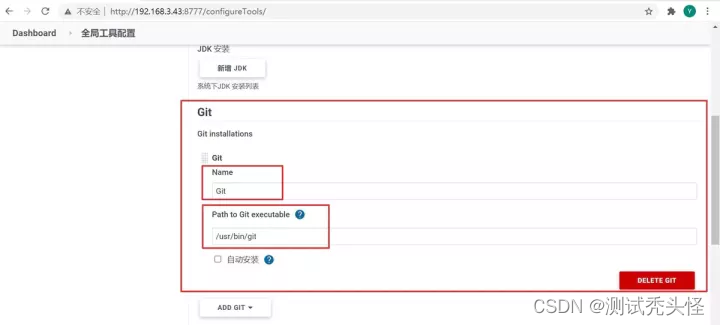
配置 Git
3、新建一个项目(选择“构建一个自由风格的软件项目”即可),进入该项目的配置页面,进行一些常规配置:

常规配置 - 配置构建该项目所要使用的节点
4、进行项目配置中的“源码管理”配置,配置后保存:
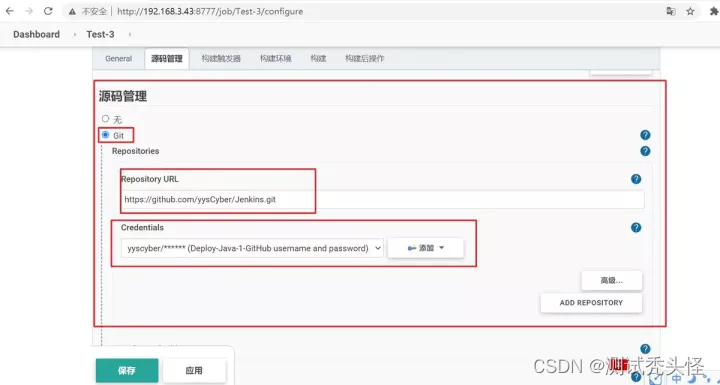
源码管理
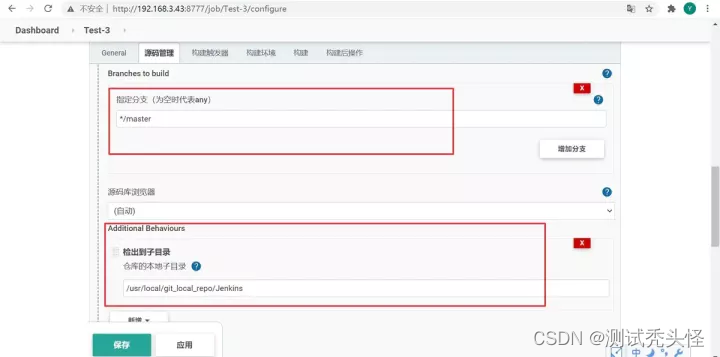
源码管理
- 勾选Git;
- 输入远程仓库的 URL,注意这个 URL 是 Clone 操作(git clone)所用的那个 URL;
- 凭据,与创建、配置“节点”时类似,已经添加过就直接选择,没有的话就添加。添加的话一般常用的就是Username with password、SSH Username with private key这两种类型。Username with password就是配置你远程源码仓库的用户名和密码,比如 GitHub 的用户名和密码。SSH Username with private key就是使用密钥对,使用的前提是需要将部署了 Jenkins 的服务器中的密钥对中的公钥($User_home_directory/.ssh/······_pub)配置在远程源码仓库中,然后“凭据”中配置密钥对中的私钥;
- 指定分支,根据实际情况;
Additional Behaviours:有很多选项供选择,类似于“构建策略”,但一般是执行在“构建策略”之前。这里选择的是“检出到子目录”,作用是从远程仓库拉取代码到本地,作用类似于git clone命令。所以,需要先在远程服务器上建立一个本地仓库目录。
5、保存项目配置,立即构建,先测试是否能从远程仓库拉取代码到本地:
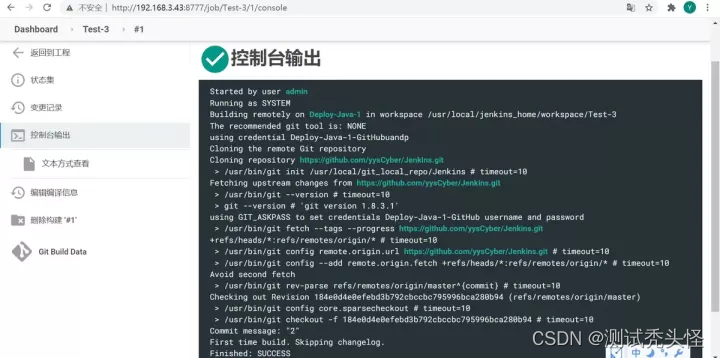
构建后控制台输出

查看本地源码仓库
上面的图说明,Git 的配置是成功的。
6、编写一个简单的用于部署的 Shell 脚本,重新回到项目的配置中,新增“构建策略”,选择“执行 Shell”,编写一个将这个 HTML 文件拷贝至 Tomcat 中的webapps/jenkins/目录下,重命名为jenkins.html。保存配置:
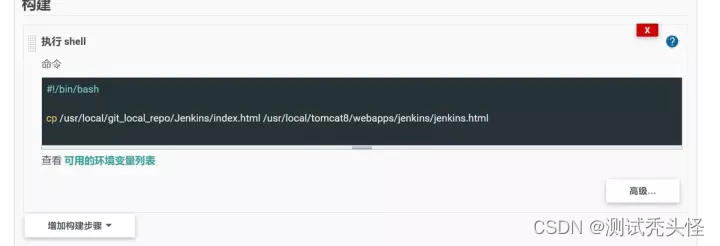
简单的部署脚本
7、先进行一次构建,一来看看 Shell 脚本是否正常运行,二是看看 HTML 页面的效果,便于与修改后区分:

HTML 页面效果
8、在 Windows 中拉取代码,编辑 HTML,来模拟开发场景,修改后提交再提交至远程仓库:
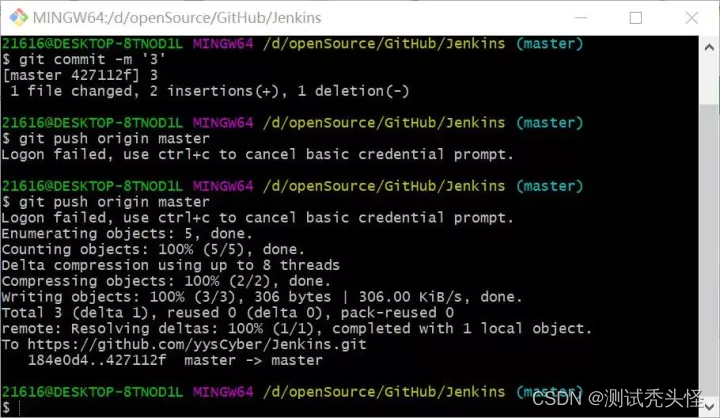
修改后提交至远程仓库
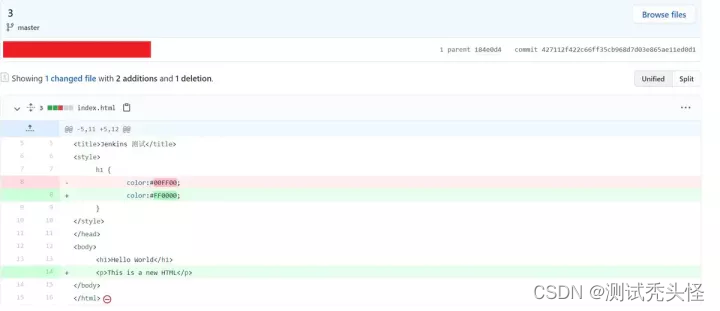
提交详情
9、再次构建,构建成功后刷新浏览器页面:
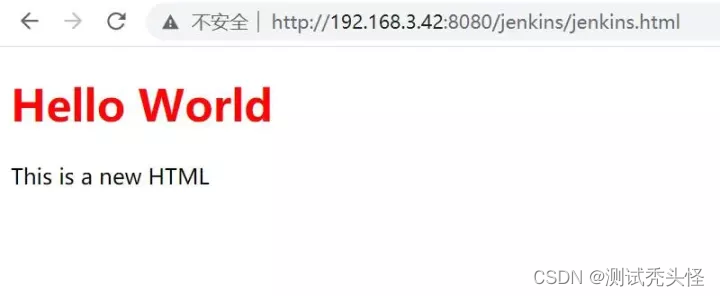
执行构建后刷新
综上,便是一个较为完整的 Jenkins 与 Git 结合使用。
三、补充
上述只是简单的示例。现实中,不论是项目复杂程度、部署的环境、部署所编写的脚本等都比示例复杂的多。希望先通过这样简单的示例,了解 Jenkins 可以与 Git 结合使用,并且对 Jenkins 可以自动拉取远程仓库中的代码并且实现部署这种常规操作不再“怀疑”即可。
最后祝大家都能找到心仪的工作,快乐工作,幸福生活,广阔天地,大有作为。PS:这里分享一套软件测试的自学教程合集。对于在测试行业发展的小伙伴们来说应该会很有帮助。除了基础入门的资源,博主也收集不少进阶自动化的资源,从理论到实战,知行合一才能真正的掌握。全套内容已经打包到网盘,内容总量接近500个G【点击文末小卡片免费领取】

☑ 240集-零基础到精通全套视频课程
☑ [课件+源码]-完整配套的教程
☑ 18套-测试实战项目源码
☑ 37套-测试工具软件包
☑ 268道-真实面试题
☑ 200个模板-面试简历模板、测试方案模板、软件测试报告模板、测试分析模版、测试计划模板、性能测试报告、性能测试报告、性能测试脚本用例模板(信息完整)
这些资料,对于做【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴我走过了最艰难的路程,希望也能帮助到你!凡事要趁早,特别是技术行业,一定要提升技术功底。
送给大家一句话,共勉:当我们能力不足的时候,首先要做的是内修!当我们能力足够强大的时候,就可以外寻了!