泰勒公式(带皮亚诺余项的n阶泰勒公式)指出了在一点可以用泰勒公式拟合出多项式函数进行无穷逼近,而因为只用到了一点n阶导数值,因此在该点n阶可导即可,是关于一个点的定性分析,一般用于求极限。

泰勒定理(带拉格朗日余项的n阶泰勒公式)只要满足闭区间连续,开区间可导,就会存在一个ξ。。。因此是类似于中值定理的逼近方法。通过在一个区间内运用中值定理,可以在满足如下条件的区间内,拟合任意一点的函数值,在闭区间内n阶导函数连续,开区间内n+1阶导函数存在(闭区间连续,开区间可导(不要求导函数连续)),一般用于大题(具体什么时候我也不记得了,可能是用高阶导数逼近函数值吧) 泰勒定理是任意地方逼近哦! 小心和泰勒级数,泰勒公式,混淆。

泰勒级数和泰勒展开式目前没有用到,以后有机会补充。
【问题思考总结】为什么一点的泰勒展开可以在任意点逼近函数?【泰勒公式 泰勒定理的适用范围】
news2026/2/15 14:05:02
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1094221.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Nginx:虚拟主机(原理+案例)
示意图: 虚拟主机
虚拟主机是一种特殊的互联网服务,让你的网站能够在互联网上被访问。通过虚拟主机,多个网站可以共享一个物理服务器的资源,包括 CPU、内存、硬盘存储和网络带宽。每个网站在虚拟主机上运行,就如同它们…
CSDN里的常用网址(2)
你问我为啥要写这篇,一是因为我自己总是记不住,二是想给大家提供便捷,懂了吧!
1、需求广场https://download.csdn.net/taskCenter/home?utm_sourceupload_qplaza_infopage_windhttps://download.csdn.net/taskCenter/home?utm_…
C++笔记之一个轻量级的线程池库threadpool
C笔记之一个轻量级的线程池库threadpool
code review!
抄自:https://github.com/lzpong/ 文章目录 C笔记之一个轻量级的线程池库threadpool1.threadpool.h2.使用:test2.cc3.使用:test1.cc4.代码 1.threadpool.h 2.使用:test2.cc…
【医学影像处理】基于MRIcron的dcm2nii批量dcm转nii格式
MRIcron下载
MRIcron下载官网 选择适合自己环境的版本,我使用的是windows版本
MRIcron介绍
MRICron是一款用于处理磁共振成像(MRI)数据的免费开源软件工具。它是一个功能强大的图像处理程序,主要用于可视化、分析和处理医学影…
代码更换了目录,没有任何变更,但Idea编辑器却提示所有代码都变更了?
开发环境:
springboot 2.4.3idea 2020 问题描述:
1、代码copy到U盘了,今天用idea打开U盘代码,却提示所有代码都被修改了 2、diff 文件看了,其实并没有任何修改,因为就算不小心误改了,也不能全…
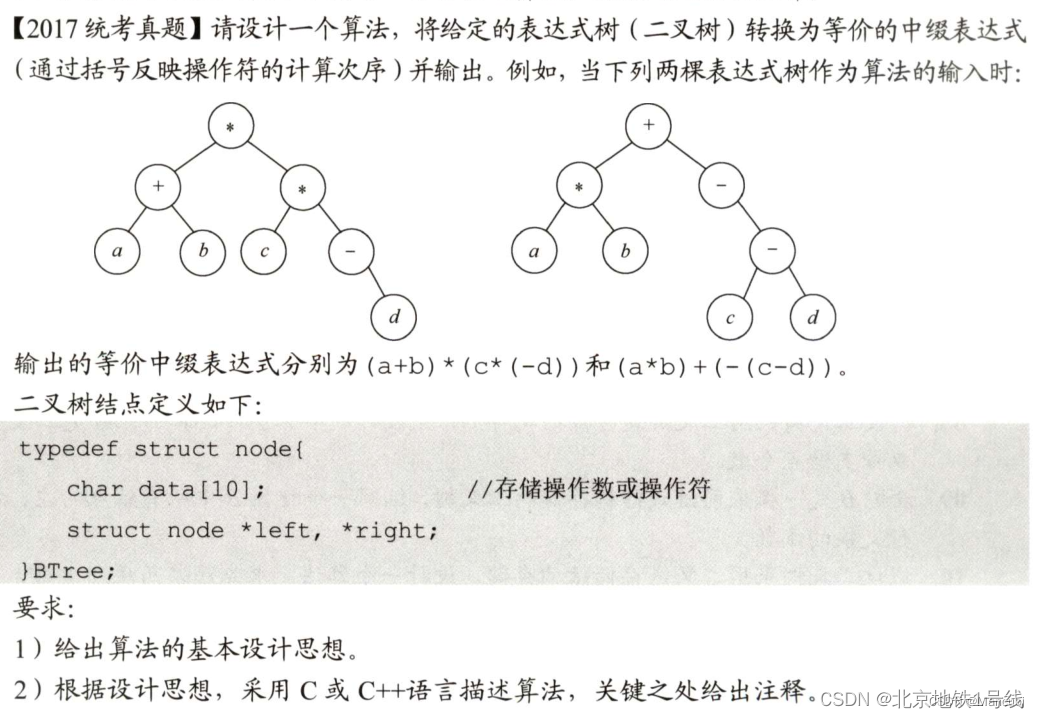
36.树与二叉树练习(2)(王道第5章综合练习)
试题1(王道5.3.3节第16题):
设计算法将二叉树的叶结点按从左到右的顺序连成单链表,连接时使用叶结点的右指针域存放单链表指针。
借助遍历算法完成:
//根据二叉树层次遍历序列构造单链表
void LevelOrdertoLinkList…
Qt事件传播机制 day8
Qt事件传播机制 day8
事件的接受和忽略
当空间忽略事件时,事件会继续往上传播,这里的传播指传播给父组件QEvent有accept()函数与ignore()函数 accept():本组件处理该事件,这个事件就不会被继续传播给其父组件ignore()࿱…
spring boot Rabbit高级教程
消息可靠性
生产者重试机制
首先第一种情况,就是生产者发送消息时,出现了网络故障,导致与MQ的连接中断。
为了解决这个问题,SpringAMQP提供的消息发送时的重试机制。即:当RabbitTemplate与MQ连接超时后,…
分类预测 | MATLAB实现SSA-CNN-LSTM-Attention数据分类预测
分类预测 | MATLAB实现SSA-CNN-LSTM-Attention数据分类预测 目录 分类预测 | MATLAB实现SSA-CNN-LSTM-Attention数据分类预测分类效果基本描述模型描述程序设计参考资料 分类效果 基本描述 1.MATLAB实现WOA-CNN-LSTM-Attention数据分类预测,运行环境Matlab2021b及以…
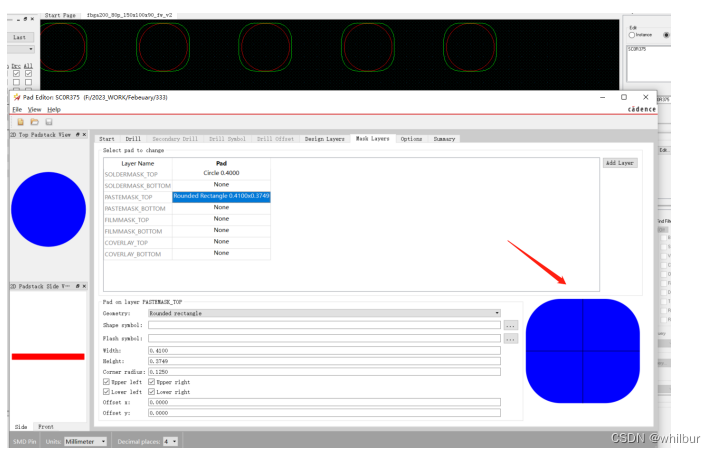
Marin说PCB之BGA焊盘削焊盘带来的焊接问题和解决办法
每周日上午10点钟都是小编最开心的时间了,这个点是斗破苍穹播出的时间。小编我从萧炎从这个动漫开播到现在都追了好多年了,强烈推荐喜欢这个小说的可以看这个动漫,拍的还不错,只是萧炎的配音不再是张沛老师了,有点可惜…
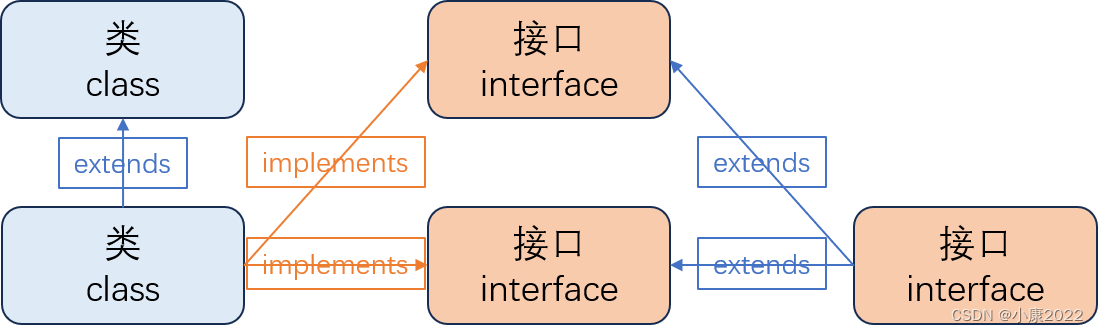
Java 继承与实现
一、继承(extends)
1.1 继承概念
继承是面向对象的基本特征,它允许子类继承父类的特征和行为,以提高代码的复用率和维护性等。下面一张图生动地展示了继承和类之间的关系: 继承图 上图中,“动物”、“食草…
【Vue面试题二十一】、Vue中的过滤器了解吗?过滤器的应用场景有哪些?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:Vue中的过滤器了解吗&am…
成为数据分析师要具备什么能力——功法篇(上)
这篇文章适合做了一段时间数据分析工作,开始思考怎么继续提升自己的分析师、运营或者是实习了一段时间的同学,这时的你也许会想几个问题: 为什么我做出来的分析总觉得没有别人的那么高级? 老板为什么总说我的分析“太浅了”&#…
spyder切换conda环境(成功测试)
今天第一次把这个anaconda中配套的spyder的切换环境尝试成功了,特地记录一下
首先明确一点我使用的最新的anaconda的版本是 spyder已经是版本5了,之前的4版本总是出现各种错误
Step1
切换python interpreter 环境是可以直接识别的,不需要…
2023-2024-1 for循环-1(15-38)
7-15 输出闰年
输出21世纪中截止某个年份以来的所有闰年年份。注意:闰年的判别条件是该年年份能被4整除但不能被100整除、或者能被400整除。
输入格式:
输入在一行中给出21世纪的某个截止年份。
输出格式:
逐行输出满足条件的所有闰年年份,即每个年…
华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍
华为端到端战略管理体系(DSTE开发战略到执行)的运作日历图/逻辑图及DSTE三大子流程介绍
本文作者 | 谢宁,《华为战略管理法:DSTE实战体系》、《智慧研发管理》作者 添加图片注释,不超过 140 字(可选&#…
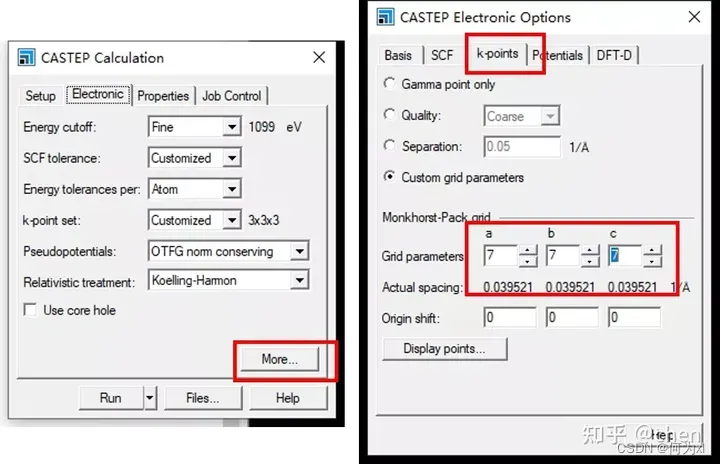
【VASP】KPOINTS文件介绍
【VASP】KPOINTS文件介绍 一、KPOINTS 的两种结构第一种结构:(非对称)第二种结构:(高对称) 二、关于KPOINTS设置的一些经验三、KPOINTS的选取 前言 一、4个常用的输入文件INCAR、POSCAR、POTCAR、KPOINTS I…
MySQL [基础]] 学习笔记
MySQL 学习 文章目录 MySQL 学习1. 数据库三层结构2. 数据在数据库中的存储方式3. SQL 语句分类3.1 备份恢复数据库的表 4. Mysql 常用数据类型(列类型)4.1 数值型(整数)的基本使用4.2 数值型(bit)的使用4.3 数值型(小数)的基本使用4.4 字符串的基本使用(面试题)4.5 字符串使用…
基于springboot实现心灵治愈心理健康平台系统项目【项目源码+论文说明】
基于springboot实现心灵心理健康平台系统演示 摘要
本论文主要论述了如何使用JAVA语言开发一个心灵治愈交流平台 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论…








![MySQL [基础]] 学习笔记](https://img-blog.csdnimg.cn/img_convert/9b4e96f14b334224361be4ca9cb56f3d.png)
