
一、说明
二、总体与样本个体统计
总体是研究人员想要研究或得出结论的整个群体或一组个人、物体或事件。它可以是人,动物,植物,甚至是无生命的物体,具体取决于研究的背景。总体通常表示完整的可能数据点或观测值集。样本:
样本是选择进行研究的总体子集。这是一个较小的群体,旨在代表较大的人口。研究人员从样本中收集数据,并用它来推断整个人口。由于从人口的每个成员收集数据通常是不切实际或不可能的,因此样本被用作收集信息的有效且具有成本效益的方法。
2.1 参数与估计
参数:参数是描述总体特征的数值。参数通常使用希腊字母表示,例如μ (mu) 表示总体均值,σ (sigma) 表示总体标准差。由于通常很难或不可能从整个总体中获取数据,因此参数通常是未知的,必须根据可用的样本数据进行估计。
统计量:统计量是描述样本特征的数值,样本是总体的子集。通过使用从代表性样本计算的统计数据,研究人员可以推断出未知的总体相应参数。常见的统计量包括样本均值(用 表示为 ,发音为“x-bar”)、样本中位数和样本标准差(用 s 表示)。
2.2 推论统计
推论统计是统计学的一个分支,专注于根据从该总体中获取的数据样本对更大的人口进行预测、估计或概括。它涉及使用概率论通过分析较小的子集或样本来推断并得出有关总体特征的结论。推论统计背后的关键思想是,从人口的每个成员收集数据通常是不切实际或不可能的,因此我们使用具有代表性的样本来推断整个群体。推论统计技术包括假设检验、置信区间和回归分析等。这些方法可帮助研究人员回答以下问题:
a。两组之间有显著差异吗?
b.我们可以根据其他变量的值预测变量的结果吗?
c. 两个或多个变量之间的关系是什么?
推论统计广泛应用于经济学、社会科学、医学和自然科学等各个领域,以根据有限的数据做出明智的决策和指导政策。
2.3 点估计
点估计值是用于根据样本数据估计总体的未知参数的单个值。例如,如果要估计特定学校中所有学生的平均身高,则可以随机抽取 100 名学生并计算该样本的平均身高。计算出的样本平均身高是学校所有学生平均身高的点估计值。
假设样本中 100 名学生的平均身高为 5 英尺 7 英寸。这是对学校所有学生平均身高的点估计。但是,请务必注意,此估计值会受到采样误差的影响,这意味着它可能与真实总体参数不完全相同。
要提高估计值的准确性,您可以增加样本数量或使用更具代表性的样本。您还可以计算一个值范围(称为置信区间),其中包括具有特定置信度的真实总体参数。
三、置信区间
置信区间是根据样本数据计算的值范围,可能包含具有一定置信度的真实总体参数。这是一种估计点估计精度并量化估计周围不确定性的方法。
例如,假设您要估计某个国家/地区所有男性成年人的平均体重。您随机抽取 100 名男性成年人,并计算出他们的平均体重为 180 磅。但是,由于随机抽样变化,真实总体参数可能略高于或低于此估计值。
要计算总体平均权重的 95% 置信区间,应使用考虑样本数量、样本均值和样本标准差的公式。生成的区间将是真实总体参数可能位于 95% 置信度范围内的估计值。
95%置信区间意味着,如果我们用不同的样本多次重复这项研究,95%的结果区间将包含真实的总体参数。
例如,总体平均权重的 95% 置信区间可以计算为 175 到 185 磅,这意味着我们对真实总体平均权重介于这两个值之间的置信度为 95%。
置信区间在统计学中广泛用于估计点估计的精度并推断总体参数
四、置信水平
置信水平是计算的置信区间包含真实总体参数的确定性或概率。它通常表示为百分比或十进制值。
例如,95% 的置信水平意味着如果我们多次重复采样和估计过程,则生成的置信区间的 95% 将包含真实的总体参数。
换句话说,较高的置信水平意味着计算的置信区间包含真实总体参数的确定性更高。但是,增加置信水平也会增加区间的宽度,从而降低估计值的精度。
通常,统计推断中最常用的置信水平是 90%、95% 和 99%。置信水平的选择取决于人们愿意接受的错误推断的风险水平。置信水平越高,确定性越高,但需要更大的样本量,并导致更宽的置信区间
五、置信区间=点估计裕度
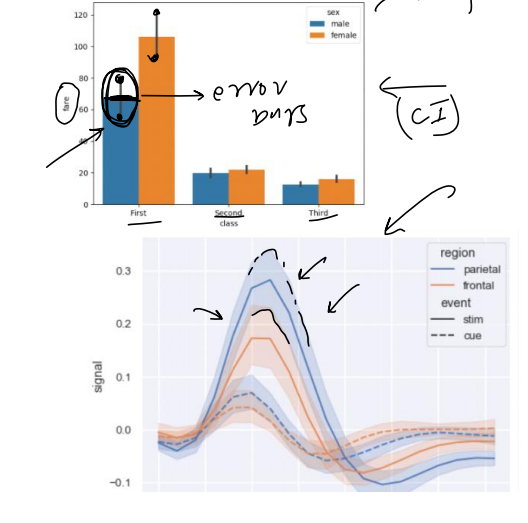
5.1 置信区间(已知西格玛)也称为 Z 过程。
当总体标准差 (sigma) 已知时,可以使用以下公式计算总体均值的置信区间:
CI=样本平均误差幅度
CI = x̄ ± Zα/2 * σ/√n
哪里:
- CI 是总体均值的置信区间
- x̄ 是样本均值。
- Zα/2 是对应于所需置信水平的标准正态分布的临界值(例如,1% 置信水平为 96.95)
- 总体标准差σ
- n 是样本数量
5.2 例如
假设您要估计已知标准差为 10,000 美元的人口的平均收入。您随机抽取 50 人,并计算出他们的平均收入为 60,000 美元。使用 95% 置信水平时,临界值 Zα/2 为 1.96。代入这些值,总体平均收入的置信区间为:
CI = 60,000 ± 1.96 * 10,000/√50 = 60,000 ± 1,385.6 = (58,614.4, 61,385.6)
因此,根据此样本,我们 95% 的置信度,真实人口平均收入在 58,614.4 美元到 61,385.6 美元之间。
请注意,此公式假定样本是从正态分布或足够大的样本数量 (n≥30) 中随机选择的,没有强烈的偏度或异常值。
六、假设
随机抽样:必须使用随机抽样方法收集数据,以确保样本具有总体代表性。这有助于最大限度地减少偏差,并确保结果可以推广到整个人群。
已知总体标准差: 必须知道或准确估计总体标准差 (σ)。在实践中,总体标准差通常是未知的,样本标准差用作估计值。但是,如果样本数量足够大,则样本标准差可以提供相当准确的近似值。
正态分布或大样本量: Z 过程假定基础总体呈正态分布。但是,如果总体分布不正态,则可以在样本量较大时应用中心极限定理(通常,样本量 n ≥ 30 被认为足够大)。根据中心极限定理,样本均值的抽样分布将接近正态分布,如
七、影响误差幅度的因素
边际误差是统计估计中由于随机抽样变化而预期的误差量。误差幅度受多种因素影响,包括:
样本数量:样本量越大,误差幅度越大,因为它减少了抽样变异。
置信水平:较高的置信水平会增加边际误差,因为它会扩大置信区间。
总体大小:较小的总体大小会增加边际误差,因为它会减少有效样本数量。
总体变异性:总体变异性越大,误差幅度越大,因为它增加了抽样变异。
抽样方法:与简单的随机抽样相比,某些抽样方法(如分层抽样或整群抽样)可能会降低误差幅度。
样本中的偏差:如果样本有偏差,则误差幅度可能会增加,因为样本不能准确代表总体。
无应答率:较高的无应答率可能会增加误差幅度,因为它会减少有效样本量并可能引入偏倚。
在设计研究或解释统计估计结果时,考虑这些因素非常重要。通过了解影响误差幅度的因素,我们可以更好地解释统计估计的精度和准确性,并做出更明智的决策。
八、T 过程
t 检验是一种统计过程,用于检验样本的均值是否与已知或假设的总体均值显著不同。当总体标准差未知且样本数量较小(小于 30)时使用。
8.1 下面介绍了如何分五个步骤进行 t 检验:
- 陈述零假设和备选项假设。原假设 (H0) 是样本均值与总体均值之间没有显著差异的陈述。备择假设 (Ha) 是样本均值与总体均值之间存在显著差异的陈述。
- 确定显著性水平 (alpha) 和自由度。Alpha 是犯类型 I 错误的概率,即在原假设为真时拒绝原假设。自由度 (df) 取决于样本数量,等于 n-1。
- 计算检验统计量 (t)。检验统计量使用公式 t = (x̄ — μ) / (s / √n) 计算,其中 x̄ 是样本均值,μ是总体均值(假设或已知),s 是样本标准差,n 是样本数量。
- 确定 t 的临界值。该值是从具有 n-1 个自由度和所需显著性水平 (alpha) 的 t 分布表中获得的。
- 做出决定并解释结果。如果 t 的绝对值大于 t 的临界值,则否定原假设并得出样本均值与总体均值之间存在显著差异的结论。如果 t 的绝对值小于 t 的临界值,则无法否定原假设并得出样本均值与总体均值之间没有显著差异的结论。
例如,假设研究人员想要测试新的饮食计划是否有效减轻体重。随机选择15个人的样本,并记录他们在饮食计划之前和之后的体重。已知饮食计划前的人口平均体重为 175 磅,标准差为 12 磅。研究人员想要检验新的饮食计划导致体重在 0.05 显著水平上显着下降的假设。
- 原假设和备择假设为:
H0:μ=175(饮食计划前的平均体重与总体平均体重之间没有显著差异) Ha:μ <175(饮食计划后体重明显下降)
- Alpha 为 0.05,自由度为 15–1 = 14。
- 计算检验统计量:
t = (x̄ — μ) / (s / √n) = (170–175) / (12 / √15) = -2.31
其中 x̄ = 170,s = 12,n = 15。
确定 t 的临界值:
从具有 14 个自由度和 0.05 显著性水平的 t 分布表中,t 的临界值为 -1.76。
由于t的绝对值(-2.31)大于t的临界值(-1.76),因此我们拒绝原假设,并得出结论,饮食计划后体重显着下降。我们可以将结果解释如下:在0.05的显著性水平上,证据表明新的饮食计划导致体重显着下降。阿贾梅塔







![[爬虫练手]学校院系专业整理](https://img-blog.csdnimg.cn/6bce7fa4a00a41e2b8b7714a4be41e24.png)


