目录
1.题目解析
2.讲解算法原理
2.1.如何来解决汉诺塔问题?
2.2.为什么这道题可以用递归来做?
2.2.1 什么是递归
2.2.2 为什么会用到递归
3.如何编写递归代码?
4.递归的细节展开图
1.题目解析
汉诺塔问题链接
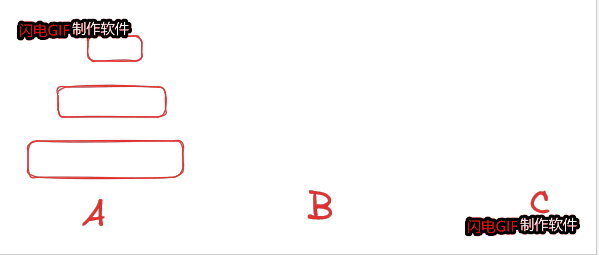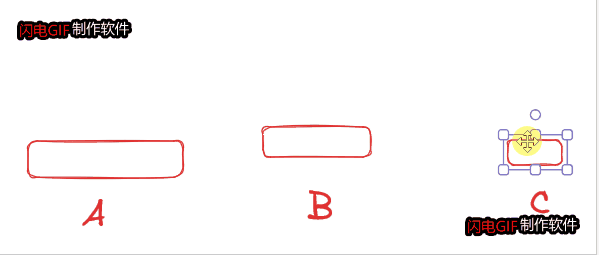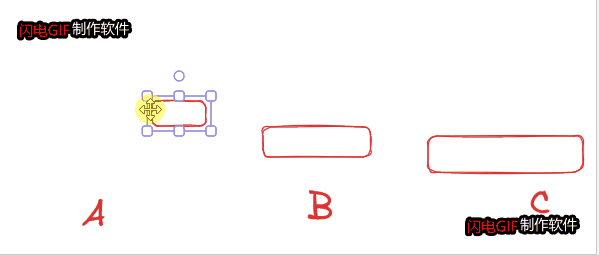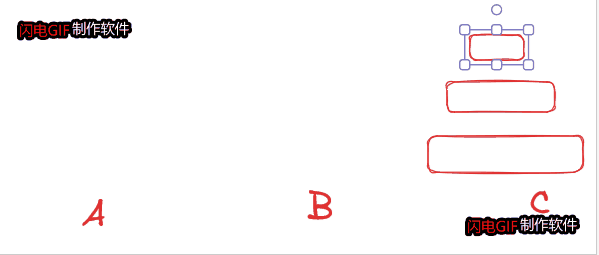
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = [] 输出:C = [2, 1, 0]示例2:
输入:A = [1, 0], B = [], C = [] 输出:C = [1, 0]
2.讲解算法原理
2.1.如何来解决汉诺塔问题?
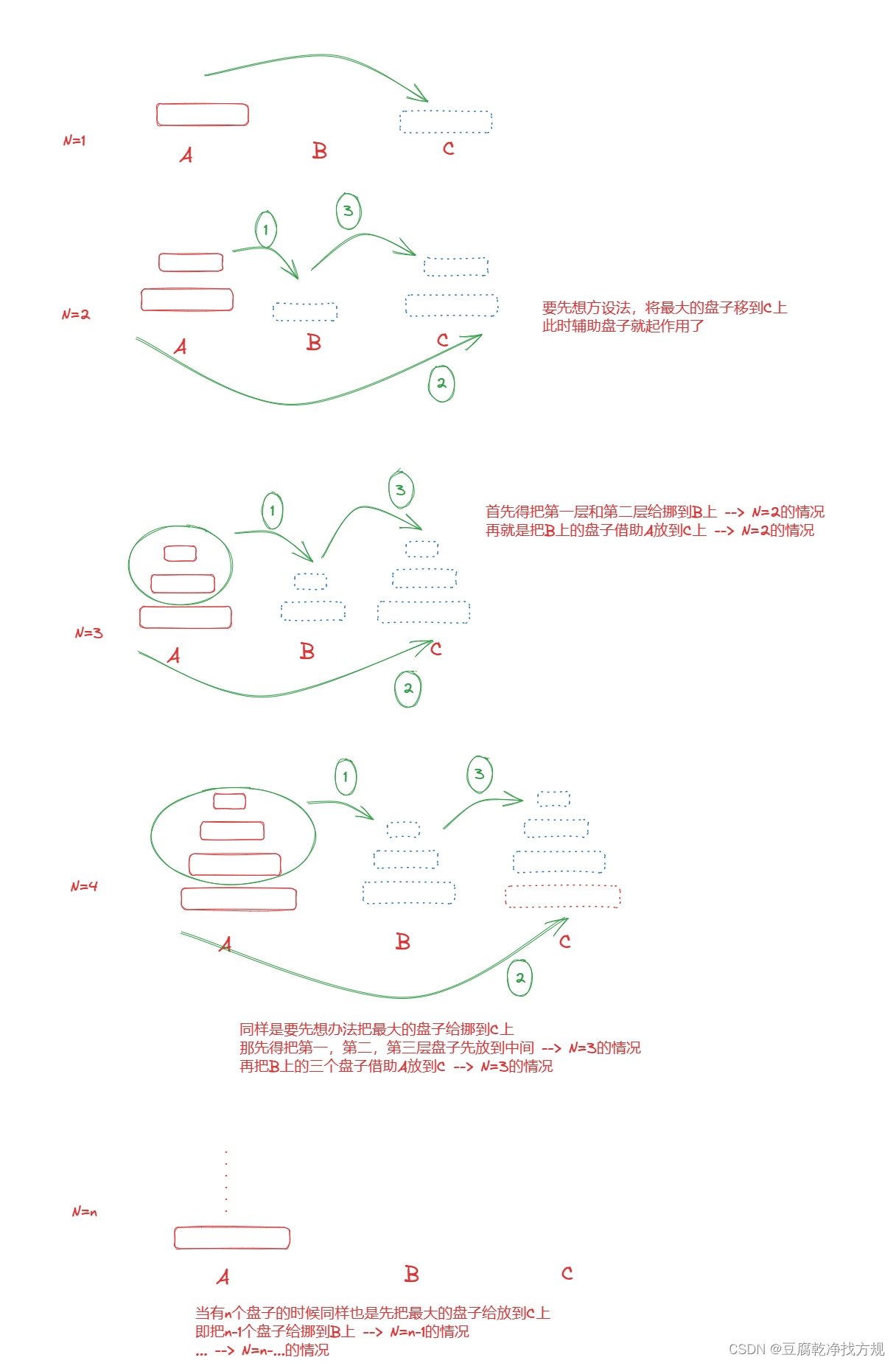
2.2.为什么这道题可以用递归来做?
2.2.1 什么是递归
函数自己调用自己的情况
2.2.2 为什么会用到递归
在解决主问题的时候碰到相同的子问题
在解决子问题的时候又碰到相同的主问题

大家发现我们的 第一个步骤和第三个步骤 全都是同样一类的问题解决 N=4 的方法和 N=3 的方法是一模一样 --> 先把除最大的盘子外的其他盘子转移到中间,后把最大盘子转到C

3.如何编写递归代码?
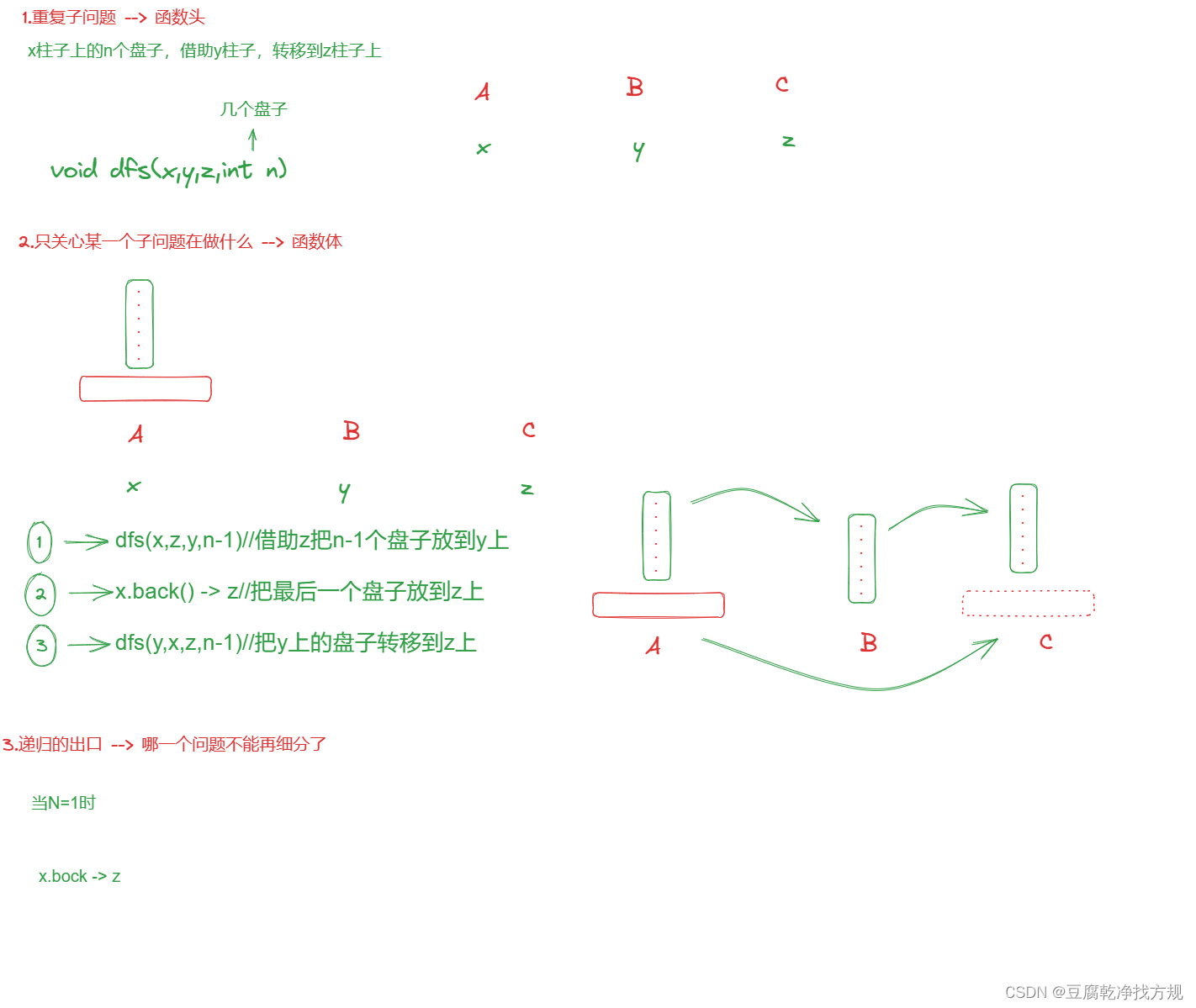
public class hanota {
public void hanota(List<Integer> a, List<Integer> b, List<Integer> c) {
dfs(a,b,c,a.size());
}
public void dfs(List<Integer> a, List<Integer> b, List<Integer> c,int n){
if (n == 1){
// 把 a 柱子的最后一个盘子移动到c
c.add(a.remove(a.size() - 1));
return;
}
// 把 a 上的 n-1 个盘子移动到b上
dfs(a,c,b,n-1);
// 把 a 的最上面的那个盘子放到 c 上
c.add(a.remove(a.size() - 1));
// 把 b 上 n-1 个盘子通过 a 放到 c 上
dfs(b,a,c,n-1);
}
}
在这里我曾经想过:为什么c.add这里是 a.siez() - 1 而不是a[0]
后来才明白:a[指的永远是最大的那个盘子,而 a.siez() - 1 指的是a最上面哪一个盘子
不能指定最大的那个盘子,因为在后续遍历中传入dsf的a不一定就是原a了,如果一直加a[0]会出现很多错误!!
4.递归的细节展开图
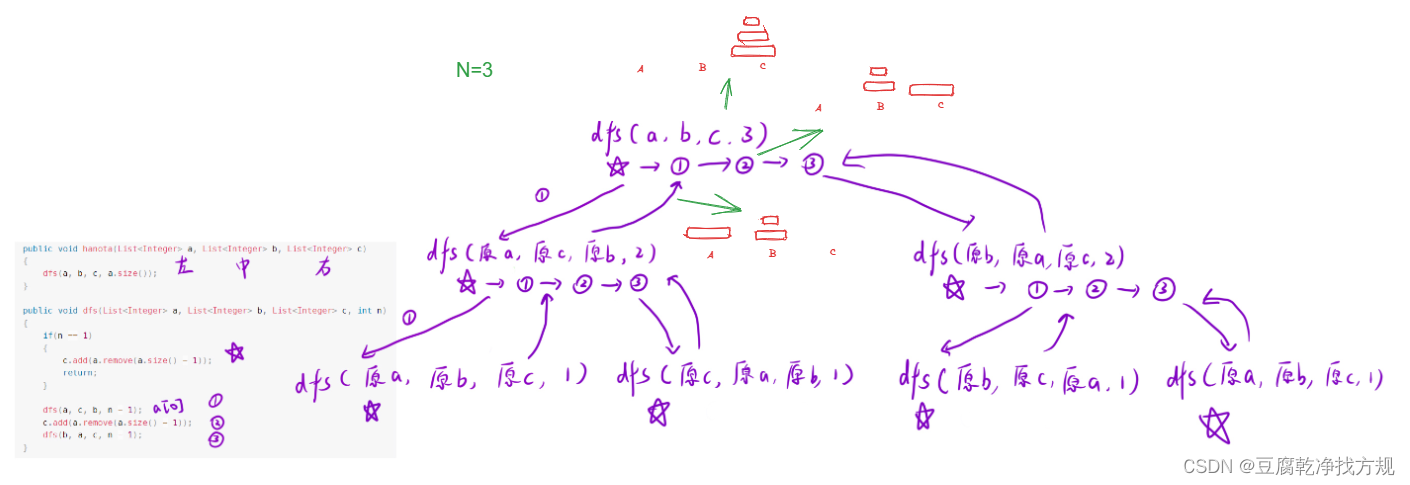













![2023年中国门把手产量、销量及市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/245f606bb9c02b8f51d6f54024a860a3.png)