随机森林属于集成学习中bagging算法的延展，所以先来介绍一下集成学习。

**集成学习：**对于训练数据集，我们通过训练一系列个体学习器，并通过一定的结合策略将它们组合起来，形成一个强有力的学习器

**个体学习器：**个体学习器是相对于集成学习来说的，作为单个学习器，它通常是由一个现有的学习算法从训练数据产生，如C4.5决策树算法、BP神经网络算法等。个体学习器代表的是单个学习器，集成学习代表的是多个学习器的结合。

Bagging与Bosting

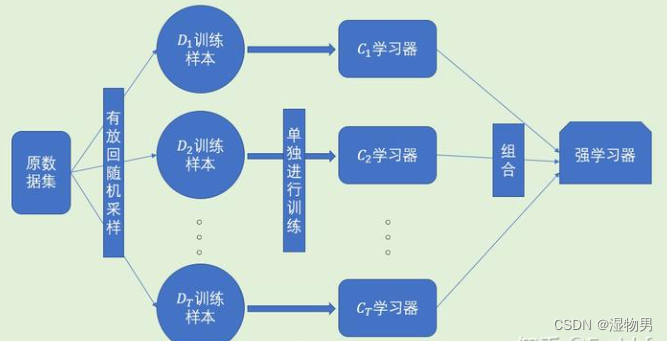
Bagging是并行式集成学习方法最著名的代表。它直接基于自助采样法(bootstrap sampling)。给定包含m个样本的数据集，我们先随机取出一个样本放入采样集中，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中，这样，经过m轮随机采样，我们得到m个样本的采样集，初始训练集中有的样本在采样集中多次出现，有的则从未出现，约63.2%的样本出现在采样集中，而未出现的约36.8%的样本可用作验证集来对后续的泛化性能进行“包外估计”。

照这样，我们可以采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，然后将这些基学习器进行结合。在对预测输出进行结合时，Bagging通常对分类任务使用简单投票法，对回归任务使用简单平均法，这就是Bagging的基本流程。

从偏差-方差分解的角度看，Bagging主要关注降低方差，因此它在不剪枝的决策树、神经网络等易受到样本扰动的学习器上效用更明显。

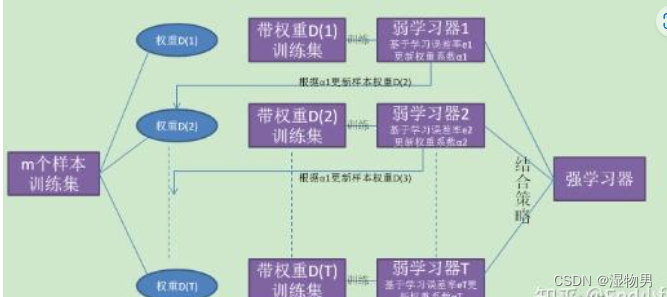
Boosting是一族可将弱学习器提升为强学习器的算法。它的基本原理：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，提高被错误分类的样本的权重，降低被正确分类的样本的权重，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值T，最后将这T个基学习器进行加权结合。

• Bagging是个体学习器不存在强依赖关系，可以同时生成的并行化方法；Boosting是个体学习器间存在强依赖关系、必须串行生成的序列化方法。

• 从偏差-方差分解角度看，Bagging主要关注降低方差，而Boosting主要关注降低偏差。

组合策略

1.平均法：①简单平均法②加权平均法

• 当个体学习器性能相差较大时宜用加权平均法，而在个体学习器性能相近时宜用简单平均法。

2.投票法

①绝对多数投票法：哪类得票过半数，则预测为该类，否则拒绝预测。

②相对多数投票法：哪类得票最多，若同时多个类得票最多，则随机从中选取一个。

③加权投票法

3.学习法

当训练数据很多时，一种更为强大的结合策略是使用“学习法”，即通过另一个学习器来进行结合。Stacking是学习法的典型代表。我们把个体学习器称为初级学习器，用于结合的学习器称为次级学习器或元学习器。

Stack先从初始数据集训练出初级学习器，然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当作样例标记。

随机森林

随机森林是Bagging的一个扩展变体，在理解了Bagging方法后，随机森林学习起来就容易多了。RF在以决策树作为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中加入了随机属性的选择。具体来说，传统决策树在选择划分属性时是在当前结点的所有候选属性（假定有d个）中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该结点的候选属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分。抽取的属性数k的选择比较重要，一般推荐 $K=lo{g}_{2}d$ 。由此，随机森林的基学习器的“多样性”不仅来自样本的扰动，还来自属性的扰动，使得最终集成的泛化能力进一步增强。

随机森林特点主要是：

• 个体学习器为决策树

• 对训练样本进行采样

• 对属性进行随机采样