力控121、122、123、188、714、309。
买卖股票的第一题
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
贪心算法
在暴力解法的基础上优化,每次暴力解法都是需要找的之前最小的值,我们用一个下标标定最小值在每次循环后查看是否需要更新最小值。
//暴力枚举 O(N^2)
int maxProfit(vector<int>& prices) {
int n = (int)prices.size(), ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
ans = max(ans, prices[j] - prices[i]);
}
}
return ans;
}
//贪心解法 O(N)
int maxProfit(vector<int>& prices) {
int mini = INT_MAX;
int maxprice = 0;
for (size_t i = 0; i < prices.size(); ++i)
{
if (prices[i] > mini)
{
maxprice = max(maxprice, prices[i] - mini);
}
mini = min(mini, prices[i]);
}
return maxprice;
}
买卖股票的第二题
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。和第一题不同的是,股票的买卖次数没有了限制,但是手中只允许有一只股票。
贪心算法
class Solution {
public:
int maxProfit(vector<int>& nums) {
int start=0;
int end=0;
int ret=0;
while(end<nums.size()-1)
{
while(end<nums.size()-1&&nums[end]<nums[end+1])
{
++end;
}
ret+=nums[end]-nums[start];
start=end+1;
end=start;
}
return ret;
}
};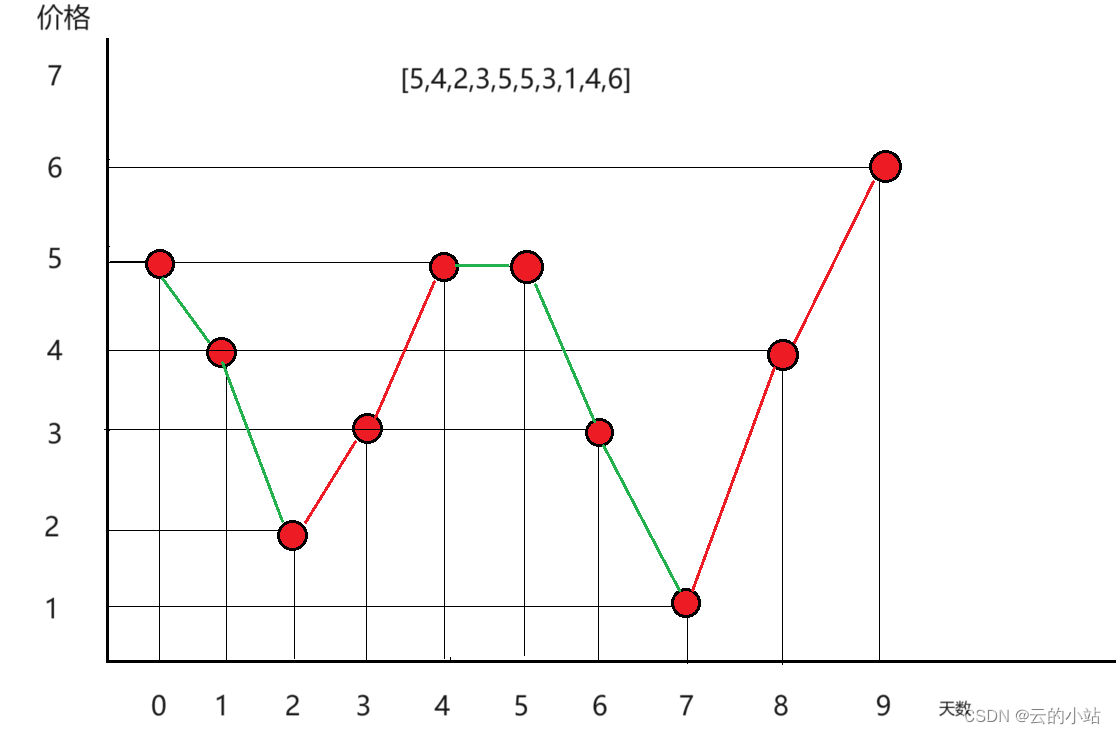
将数组的所有点的都标定在二位坐标图中,会发现,线向上递增的,都是可以获得股票收益的时候。所以我们用双指针的方法标定指针向上趋势的第一个结点和最后一个结点,在相减后就是我们这段区间的获利金额。
买卖股票的第三题
123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
动态规划
状态表示:状态转移图
在第i天最大利润:买入状态、可交易状态、冷冻期状态
定义双状态,买入状态与卖出状态:F与G状态。每个状态有3个情况就是交易0、1、2次的最大获利,因为出现多状态,所以需要状态转移图。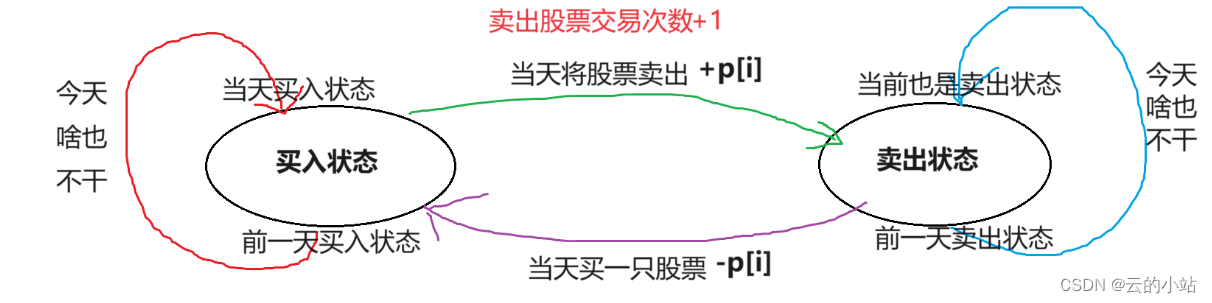
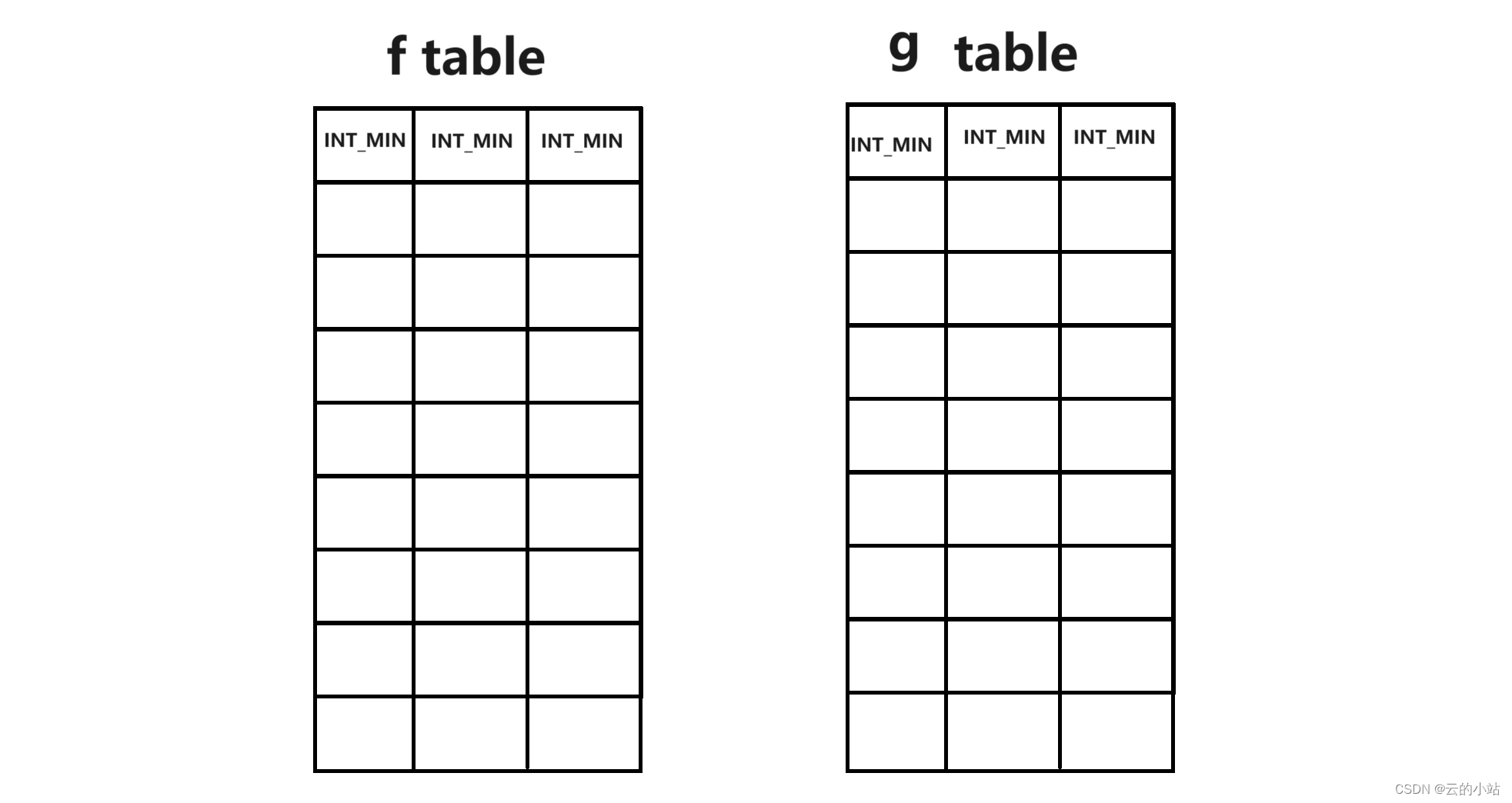
定义买入和卖出状态的dp表,因为只能完成2笔交易,所以存在完成0笔最大,1笔最大,2笔最大
vector<vector<int>>f(n,vector<int>(3,MIN));
vector<vector<int>>g(n,vector<int>(3,MIN));状态转移方程
根据状态变化图可以得出
//i位天数,j为交易次数
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
//f[i-1][j]:由昨天买入到今天买入,天数-1,交易次数不变==什么都不干
//g[i-1][j]-prices[i]:今天把股票买了,所以从昨天得卖出状态最大收益
//减去今天的股票价格,就是今天买入状态的最大收益,状态由卖出->买入状态
g[i][j]=max(g[i-1][j]],f[i-1][j-1]+prices[i]);
//g[i-1][j]: 今天啥也不干,依旧是昨天股票价格,天数-1。
//f[i-1][j-1]+prices[i]:今天把持有股票卖了,所以昨天的由昨天买入状态
//加上今天的卖出的的股票价格,就是今天卖出的最大收益,状态由买入->卖出
//如果g[i][j]=max(g[i-1][j]],f[i-1][j-1]+prices[i]);我们的对齐初始化会
//非常的麻烦,为了i-1不越界需要初始化第一行,为了j-1不越界我们初始化第一列
//初始化第一行也就固定3个数据,初始化了无所谓。
//我们可以先
g[i][j]=g[i-1][j];
//然后判断j-1>=0
if(j-1>=0)
g[i][j]=max(g[i][j]],f[i-1][j-1]+prices[i]);
初始化
我们需要初始化最开头的一行数据,因为是max取,所以我们直接将f和g首行初始化INT_MIN/2;
为什么要/2,因为最开始的-p[i]可能会导致溢出,所以我们最小值/2就好。
然后定义f[0][0]为-price[0]:第一天买入就是,买入第一天股票
然后定义g[0][0]为0:第一天卖入就是,第一天啥也不干,其实后面的g[i][0]都是0,因为第二天也啥也不干的0次交易的最大也是基础前一天的0,不能继承f[i][0-1]这个非法的东西;
返回值
在返回的时候与f表就无关了,因为f表代表手上由股票,必须把票卖掉才是最大利润。所以在g表中找最后一天结束后最大利润
#define MIN -0x3f3f3f3f
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
vector<vector<int>>f(n,vector<int>(3));
vector<vector<int>>g(n,vector<int>(3));
f[0][1]=f[0][2]=MIN;
g[0][1]=g[0][2]=MIN;
f[0][0]=-prices[0];
g[0][0]=0;
for(int i=1;i<n;++i)
{
for(int j=0;j<3;++j)
{
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
g[i][j]=g[i-1][j];
if(j-1>=0)
g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
}
}
int ret=0;
for(int j=0;j<3;++j)
{
ret=max(ret,g[n-1][j]);
}
return ret;
}
};买卖股票的第四题
309. 买卖股票的最佳时机含冷冻期
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
这其实就是第三题的演变版本
#define MIN -0x3f3f3f3f
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n=prices.size();
vector<vector<int>>f(n,vector<int>(k+1,MIN));
vector<vector<int>>g(n,vector<int>(k+1,MIN));
f[0][0]=-prices[0];
g[0][0]=0;
for(int i=1;i<n;++i)
{
for(int j=0;j<k+1;++j)
{
f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
g[i][j]=g[i-1][j];
if(j-1>=0)
g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
}
}
int ret=0;
for(int j=0;j<k+1;++j)
{
ret=max(ret,g[n-1][j]);
}
return ret;
}
};买卖股票的第五题(冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
动态规划
状态表示:状态转换图
在第i天最大利润:买入状态、可交易状态、冷冻期状态
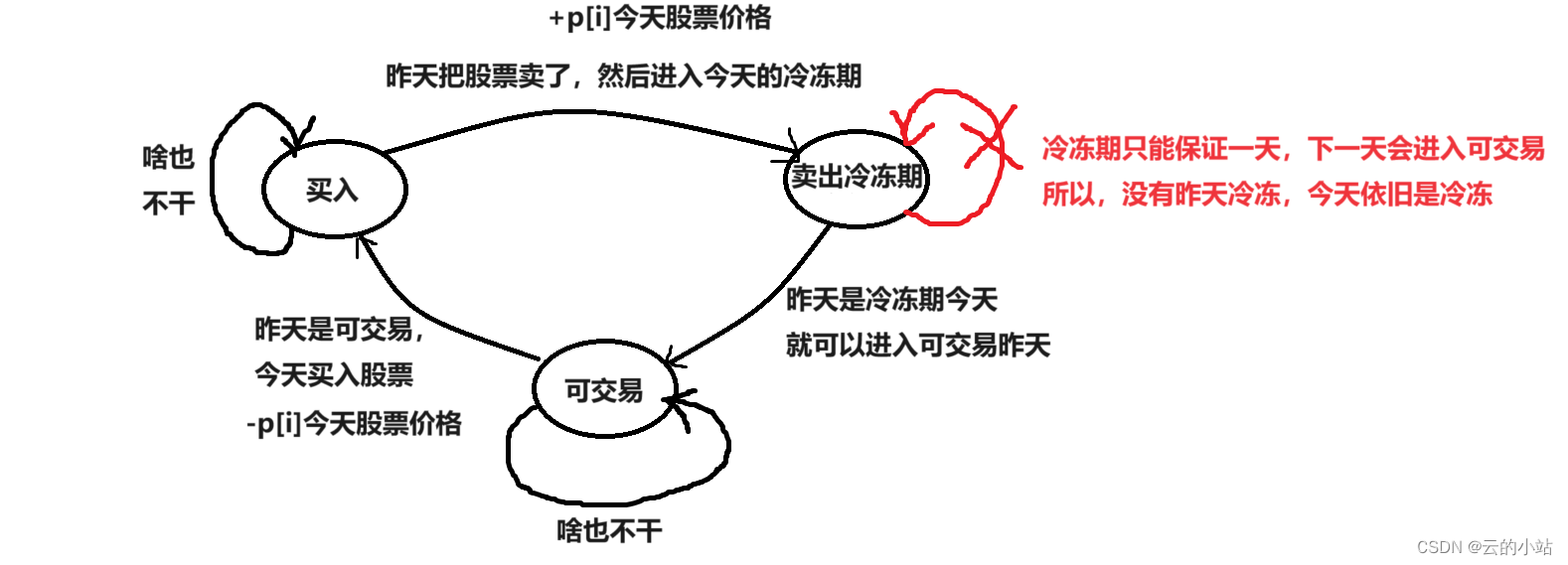
设置3个dp表:买入dp,可交易dp,冷冻dp,大小设置为股市天数。
用一个二维表吧三个表合并在一起:
-
0下标买入表 dp[i][0] 第i天时买入状态的最大利润
-
1下标交易表 dp[i][1] 第i天时交易状态的最大利润
-
2下标可冷冻表 dp[i][2]第i天时可冷冻状态的最大利润
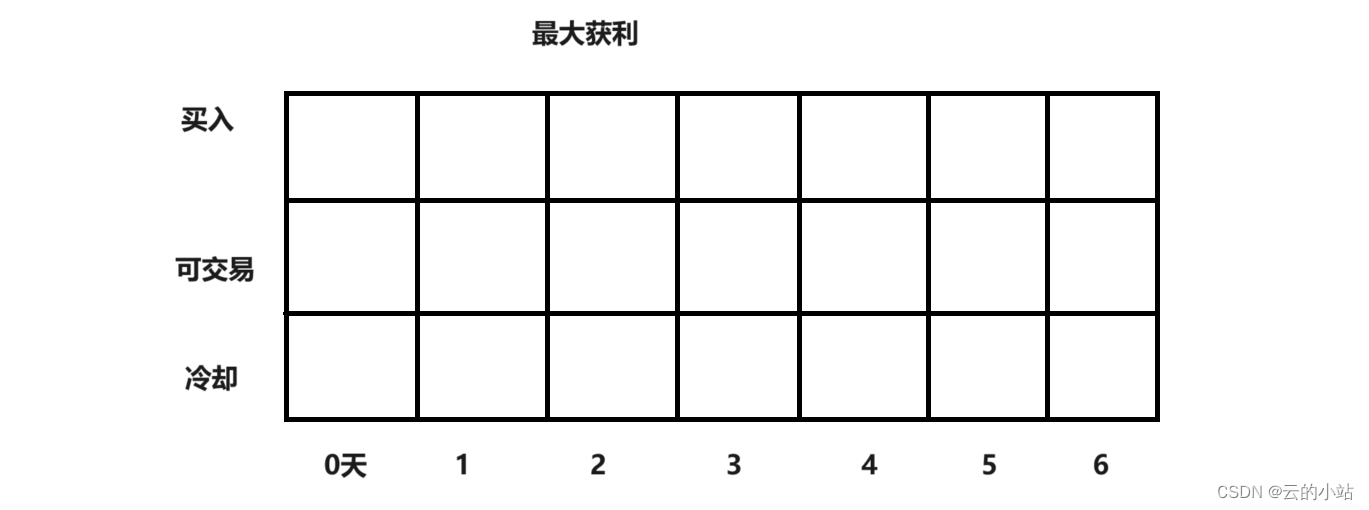
状态转移方程
根据状态转移图,箭头从前一天的某个状态到当天的某个状态得出:
- dp[i][buy]=max(dp[i-1][buy],dp[i-1][Tradable]-price[i]);
- dp[i][Tradable]=max(dp[i-1][Tradable],dp[i-1][cooling])
- dp[i][cooling]=dp[i-1][buy]+price[i];
初始化
查看转移方程,我们需要初始化第一天的所有情况dp[0][buy]、dp[0][Tradable]、dp[0][cooling]。
dp[0][Buy]=-prices[0];
dp[0][cooling]=0;
dp[0][Tradable]=0;返回值
返回cooling和Traadble最后的最大一个。
代码
class Solution {
enum state
{
Buy,
Tradable,
cooling
};
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
vector<vector<int>> dp(n,vector<int>(3));
dp[0][Buy]=-prices[0];
dp[0][cooling]=0;
dp[0][Tradable]=0;
for(int i=1;i<n;++i)
{
dp[i][Buy]=max(dp[i-1][Buy],dp[i-1][Tradable]-prices[i]);
dp[i][cooling]=dp[i-1][Buy]+prices[i];
dp[i][Tradable]=max(dp[i-1][Tradable],dp[i-1][cooling]);
}
return max(dp[n-1][Tradable],dp[n-1][cooling]);
}
};买卖股票的第六题(手续费
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
动态规划
状态表示:状态转换图
在第i天最大利润:买入状态、卖出状态。
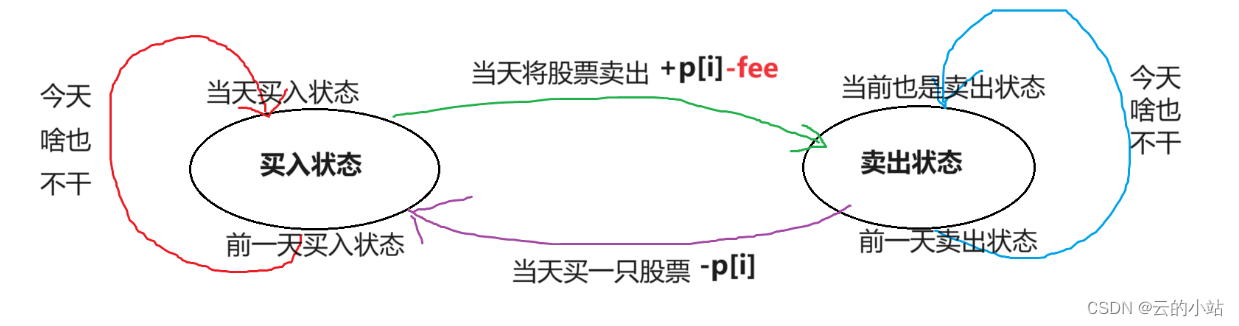
2个dp表:
-
send[i]:第i天时候卖出状态下最大的获利情况。
-
buy[i]:第i天时买入状态下最大的获利情况。
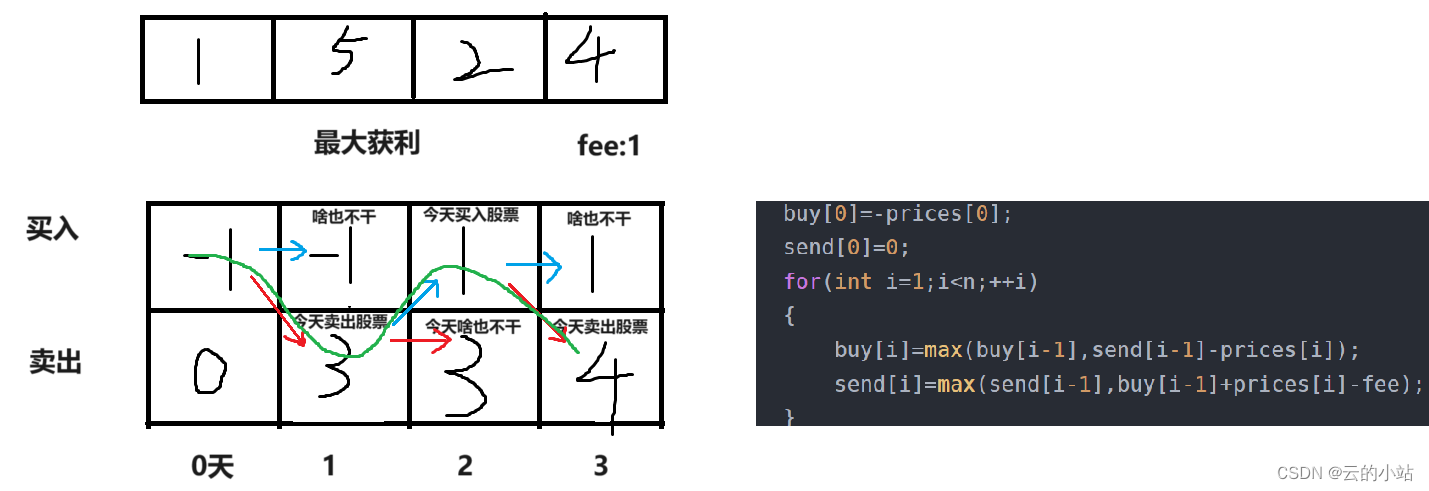
状态转移方程
buy[i]=max(buy[i-1],send[i-1]-prices[i]);
//buy[i-1]->buy[i]:昨天处于买入状态,今天依旧处于买入状态
//send[i-1]-prices[i]:昨天是卖出状态,今天买入股票,利减今日股价
send[i]=max(send[i-1],buy[i-1]+prices[i]-fee);
//send[i-1]->sned[i]:昨天处于卖出状态,今日依旧不买股票
//buy[i-1]+prices[i]-fee->send[i]:昨日买入状态,今日卖出股票,获利今日股价,交手续费fee初始化
buy[0] =-price[0]:第一天买股票。
send[0]=0:第一天不买股票。
返回值
最后一天股票卖出股票的最大值
代码
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n=prices.size();
vector<int>send(n);
vector<int>buy(n);
buy[0]=-prices[0];
send[0]=0;
for(int i=1;i<n;++i)
{
buy[i]=max(buy[i-1],send[i-1]-prices[i]);
send[i]=max(send[i-1],buy[i-1]+prices[i]-fee);
}
return send[n-1];
}
};