已知三角形的三个顶点坐标，判断某个点是否在三角形中（在三角形的边上，我们也视作在三角形中），我们提供不同的方法。

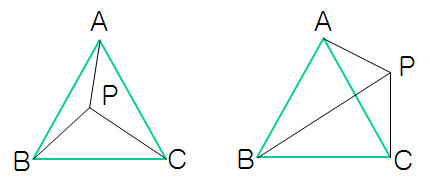
方法1：内角和等于360°

方法2：等面积法

即对于△ABC内的某一点P，连接PA、PB、PC得到三条线段，当且仅当三条线段组成的三个夹角和为360°的时候，该点才位于三角形内部。但此种方法的计算涉及到平方根、反正（余）弦，效率低。

类似的还有，P与ABC三个顶点组成的三个三角形，面积之和等于△ABC的面积，同样可以证明点P位于三角形内部，但效率也很低。

知道三个点，如何求该三个点为顶点的三角形的面积？使用海伦公式：

，其中，a，b，c表示三个边长，p表示半周长

#面积法判断点是否在三角形内
def isInside(x1, y1, x2, y2, x3, y3, x, y):
    def getSideLength(x1, y1, x2, y2):
        a = abs(x2 - x1)
        b = abs(y2 - y1)
        return math.sqrt(a*a + b*b)
 
    def getArea(x1, y1, x2, y2, x3, y3):
        a = getSideLength(x1, y1, x2, y2)
        b = getSideLength(x1, y1, x3, y3)
        c = getSideLength(x2, y2, x3, y3)
        p = (a + b + c) / 2
        return math.sqrt(p * (p-a) * (p-b) * (p-c))
 
    area1 = getArea(x1, y1, x2, y2, x, y)
    print(area1)
    area2 = getArea(x1, y1, x3, y3, x, y)
    print(area2)
    area3 = getArea(x2, y2, x3, y3, x, y)
    print(area3)
    allArea = getArea(x1, y1, x2, y2, x3, y3)
    print(allArea)
    return (area1 + area2 + area3) <= allArea
 
 

# -*- coding: utf-8 -*-
# author: Yufeng Song
import numpy as np
import random
 
 
# 定义点
class Vertex(object):
    def __init__(self, x, y):
        self.x = x
        self.y = y
 
    def __str__(self):
        return ("x坐标：%s,y坐标：%s" % (self.x, self.y))
        # "Freind : %s" %self.name 返回多个参数啊
 
 
# 定义三角形
class Triangle(object):
    def __init__(self, A, B, C):
        self.A = A
        self.B = B
        self.C = C
 
    def __str__(self):
        return ("A点：%s B点：%s C点：%s" % (self.A, self.B, self.C))
 
    # 判断构建的三角形是否满足三角形条件，即面积是否为零
    def isTriangle(self):
        arr = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
        s = abs(0.5 * np.linalg.det(arr))
        return False if s == 0 else True
 
    # 判断一个点是否在三角形内，即该点与三角形任意两点构成的面积不为0且面积和为外部大三角形面积之和
    def isInTriangle(self, D):
        arr1 = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
        sumAera = 0.5 * np.linalg.det(arr1)
        arr2 = np.array([[self.A.x, self.A.y, 1], [self.B.x, self.B.y, 1], [D.x, D.y, 1]])
        s1 = 0.5 * np.linalg.det(arr2)
        arr3 = np.array([[self.A.x, self.A.y, 1], [D.x, D.y, 1], [self.C.x, self.C.y, 1]])
        s2 = 0.5 * np.linalg.det(arr3)
        arr4 = np.array([[D.x, D.y, 1], [self.B.x, self.B.y, 1], [self.C.x, self.C.y, 1]])
        s3 = 0.5 * np.linalg.det(arr4)
        if s1 != 0 and s2 != 0 and s3 != 0 and abs(s1 + s2 + s3 - sumAera) < 0.000001:
            return True
        else:
            return False
 
 
if __name__ == '__main__':
    # 产生1000个点且存储起来
    arrOfVertex = []
    for i in range(1000):
        tempx = random.randint(1, 100)
        tempy = random.randint(1, 100)
        tempVertex = Vertex(tempx, tempy)
        arrOfVertex.append(tempVertex)
    # 在这1000个点中随机选取3个点且保证这三个点构成一个三角形
    k, j, m = random.randint(0, 999), random.randint(0, 999), random.randint(0, 999)
    selectedTriangle = Triangle(arrOfVertex[k], arrOfVertex[j], arrOfVertex[m])
    while not selectedTriangle.isTriangle():
        k, j, m = random.randint(0, 999), random.randint(0, 999), random.randint(0, 999)
 
        selectedTriangle = Triangle(arrOfVertex[k], arrOfVertex[j], arrOfVertex[m])
    # 判断点是否在三角形中，且用一个数组存储起来
    arrOfJudge = []
    sum = 0
    for i in range(1000):
        temp = selectedTriangle.isInTriangle(arrOfVertex[i])
        print(arrOfVertex[i], end="  ")
        if temp: sum += 1
        arrOfJudge.append(temp)
    print("选取的是否为三角形:%s" % selectedTriangle.isTriangle())
    print(arrOfJudge)
    print("在三角形内部的比例为：%s %%" % (sum / 10))
 
# a = Vertex(1, 1)
# b = Vertex(2, 2)
# c = Vertex(3, 3)
# print(a)
# tri = Triangle(a, b, c)
# print(tri)
# print(tri.isTriangle())

方法3：向量法（同边法）

向量法：如果点(x, y)在三角形内部，那么从某个点逆时针出发，点（x, y)都在每条边的左侧。

首先看一下这个问题，如何判断某两个点在某条直线的同一侧？

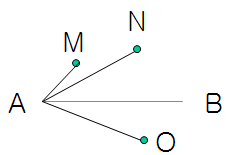
根据向量的叉乘以及右手螺旋定则，AB^AM （^表示叉乘，这里向量省略了字母上面的箭头符号）的方向为向外指出屏幕，AB^AN也是向外指出屏幕，但AB^AO的方向是向内指向屏幕，因此M,N在直线AB的同侧，M ,O在直线AB的两侧。实际计算时，只需要考虑叉积的数值正负

假设以上各点坐标为A(0,0), B(4,0), M(1,2), N(3,4), O(3,-4)， 则：

AB^AM = (4,0)^(1,2) = 4*2 - 0*1 = 8

AB^AN = (4，0)^(3，4) = 4*4 – 0*3 = 16

AB^AO = (4,0)^(3,-4) = 4*-4 – 0*3 = –16

由上面的数值可知，可以根据数值的正负判断叉乘后向量的方向。即，如果叉积AB^AM 和 AB^AN的结果同号，那么M,N两点就在直线的同侧，否则不在同一侧。特殊地，如果点M在直线AB上，则AB^AM的值为0。（如果是在三维坐标系中，求出的叉积是一个向量，可以根据两个向量的点积结果正负来判断两个向量的是否指向同一侧）                                    

以上的问题解决了，就很容易的用来判断某个点是否在三角形内，如果P在三角形ABC内部，则满足以下三个条件：P,A在BC的同侧、P,B在AC的同侧、PC在AB的同侧。某一个不满足则表示P不在三角形内部。

def isInside(x1, y1, x2, y2, x3, y3, x, y):
    def crossProduct(x1, y1, x2, y2):
        return x1 * y2 - x2 * y1

    if crossProduct(x3-x1, y3-y1, x2-x1, y2-y1) >= 0:
        x2, x3 = x3, x2
        y2, y3 = y3, y2
    if crossProduct(x2-x1, y2-y1, x-x1, y-y1) < 0:
        return False
    if crossProduct(x3-x2, y3-y2, x-x2, y-y2) < 0:
        return False
    if crossProduct(x1-x3, y1-y3, x-x3, y-y3) < 0:
        return False
    return True